
Вариант 17
Применяя подходящие подстановки, найти следующие интегралы:
1.1.![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
;
Применяя метод интегрирования по частям, найти следующие интегралы: 2.1.
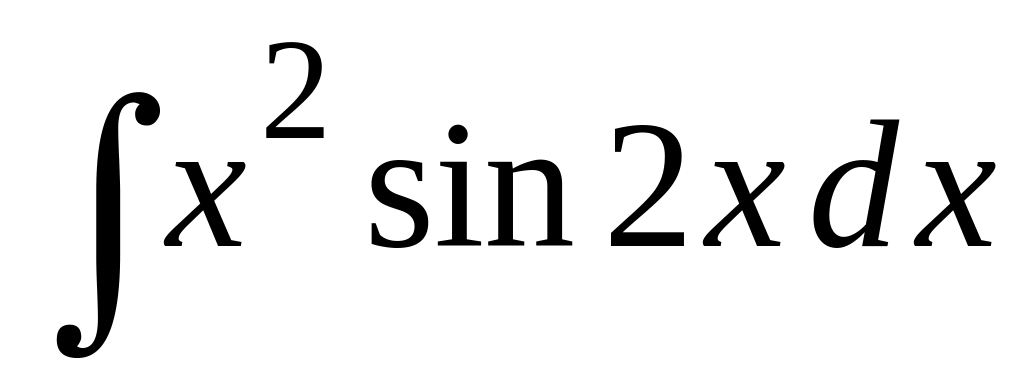 ;
2.2.
;
2.2.
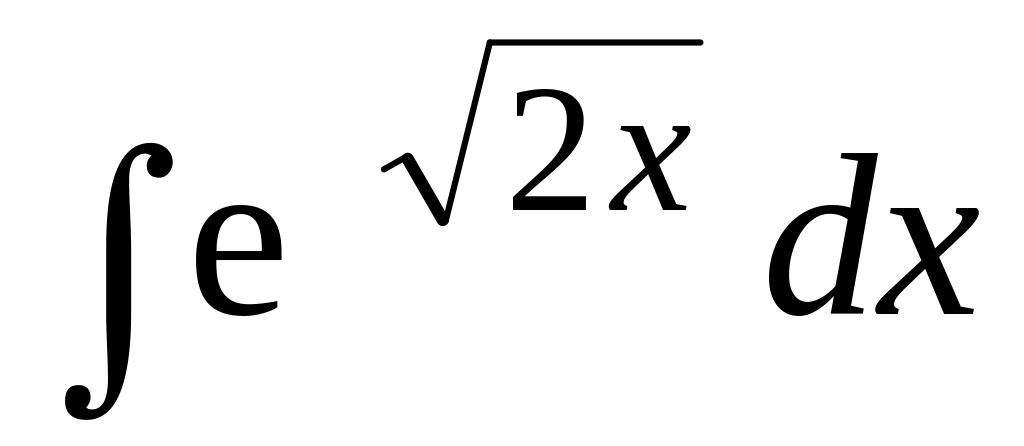 ;
2.3.
;
2.3.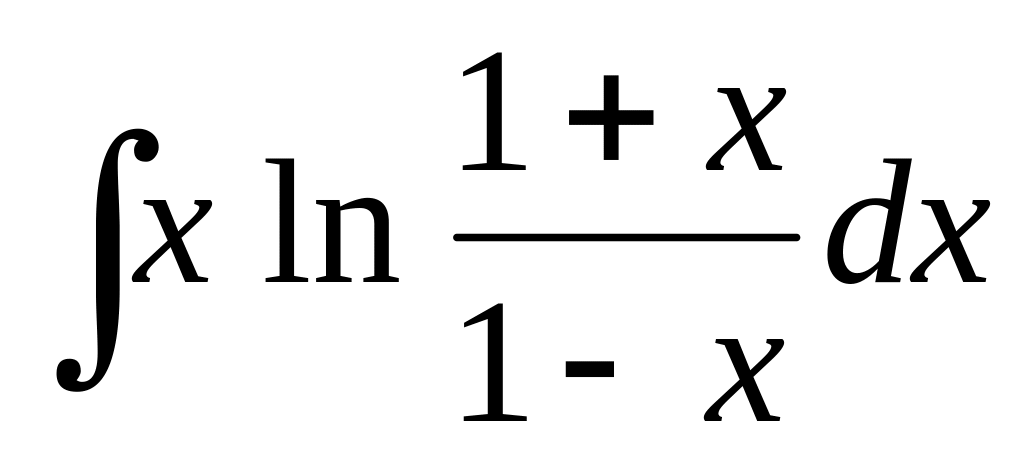 ;
;Найти неопределенный интеграл:
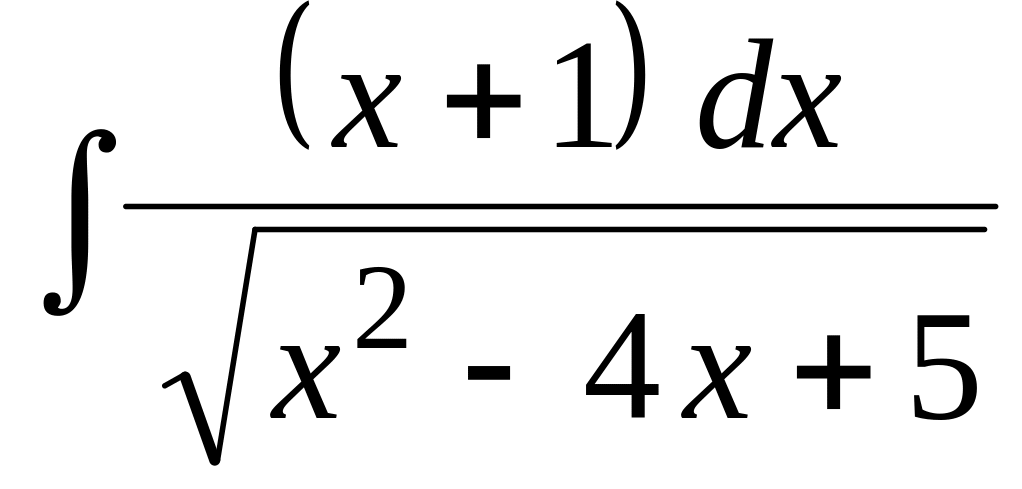 .
..Применяя метод неопределенных коэффициентов, найти интеграл:
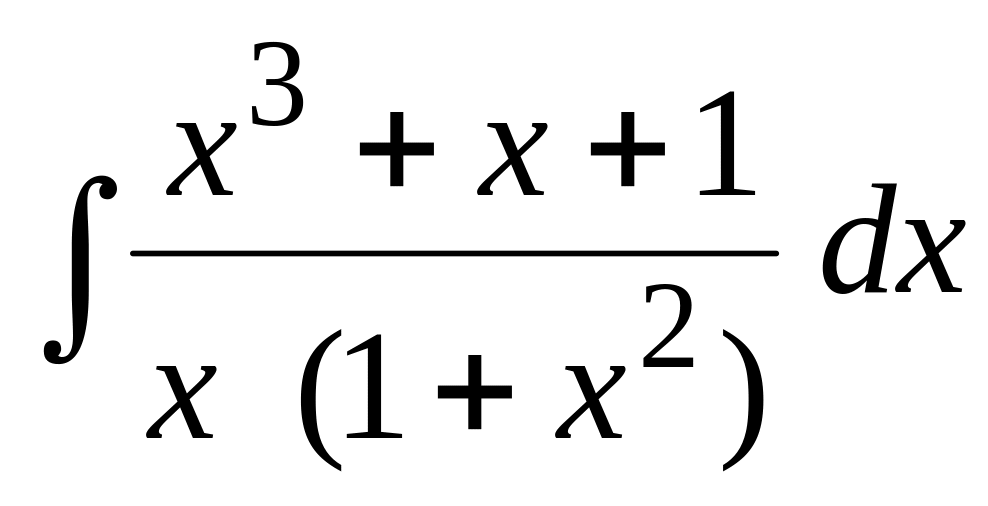
Применяя тригонометрические подстановки, найти интеграл:
![]()
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
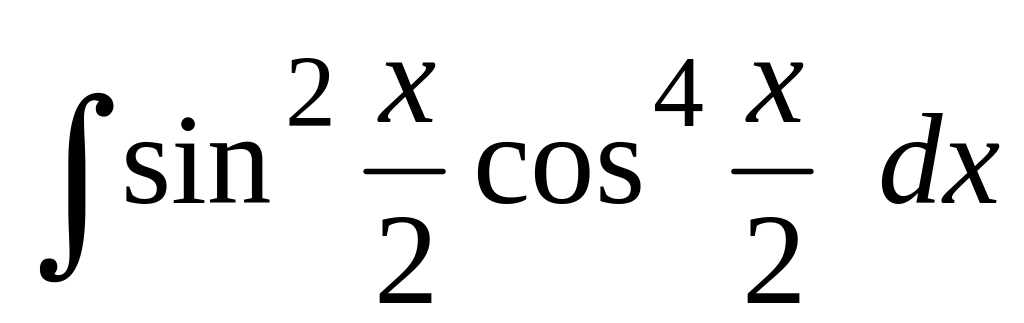 .
.Используя тригонометрические подстановки, найти интеграл:
 .
.
Вариант 18
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2.
;
1.2.![]() ;
1.3.
;
1.3.
![]() .
.
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]() .
.
Найти неопределенный интеграл:
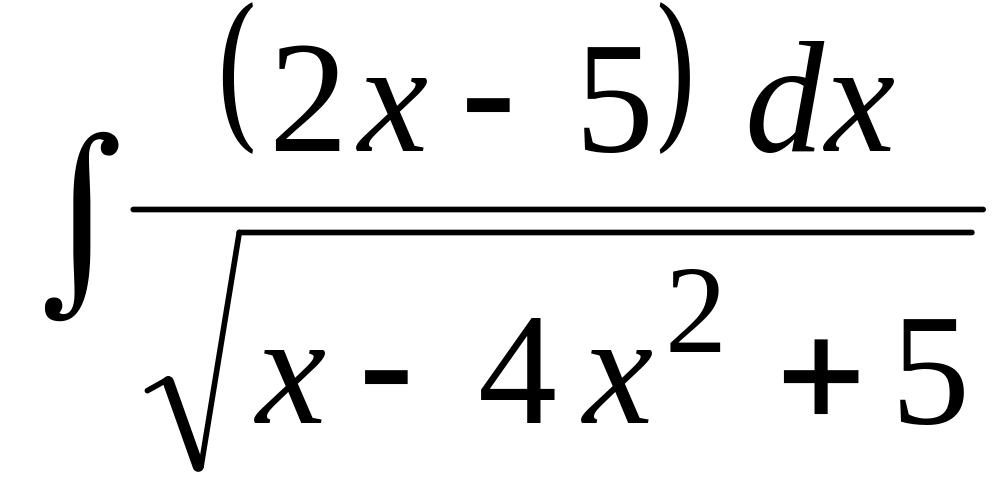 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
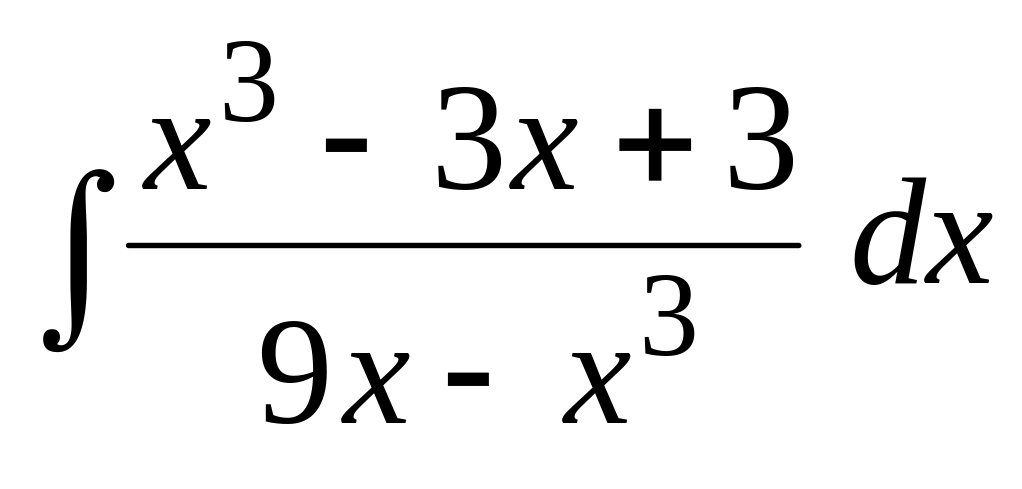 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
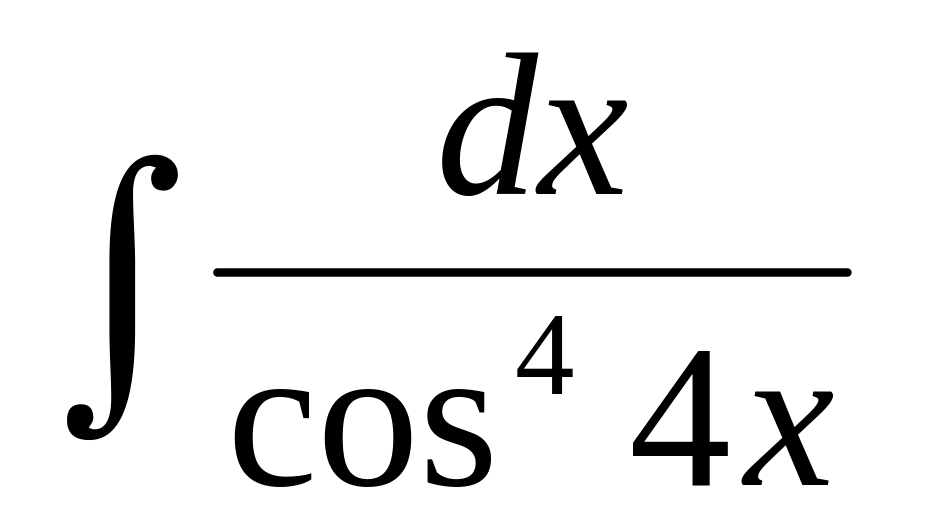 .
.Используя тригонометрические подстановки, найти интеграл:

Вариант 19
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2.
;
1.2.![]() ;
1.3.
;
1.3.
![]()
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.![]() ;
2.3.
;
2.3.
![]() ;
;
Найти неопределенный интеграл:
 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
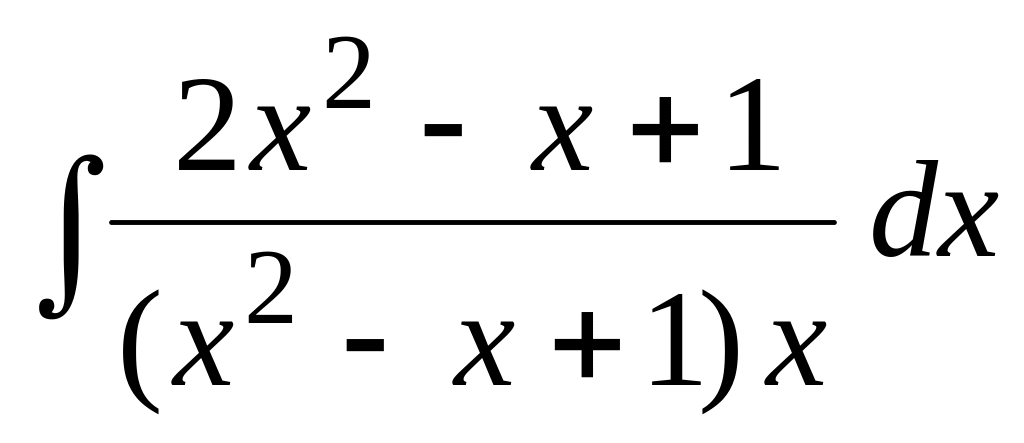 .
.Применяя тригонометрические подстановки, найти интеграл:
 .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
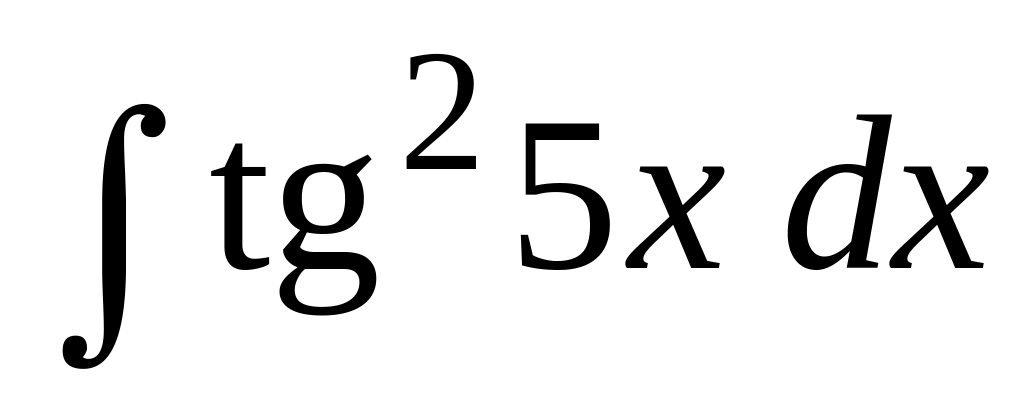 .
.Используя тригонометрические подстановки, найти интеграл:
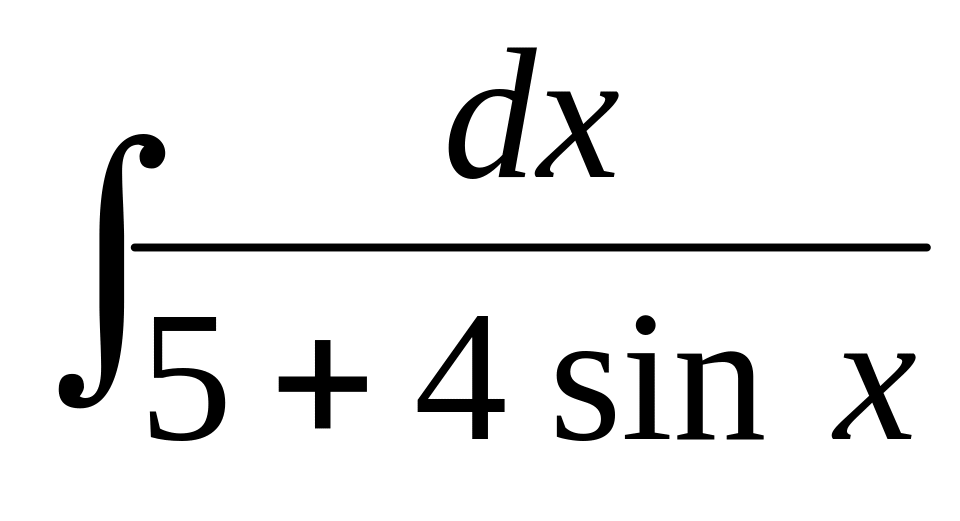 .
.
Вариант 20
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3
;
1.3![]() .
.
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.![]() ;
;
Найти неопределенный интеграл:
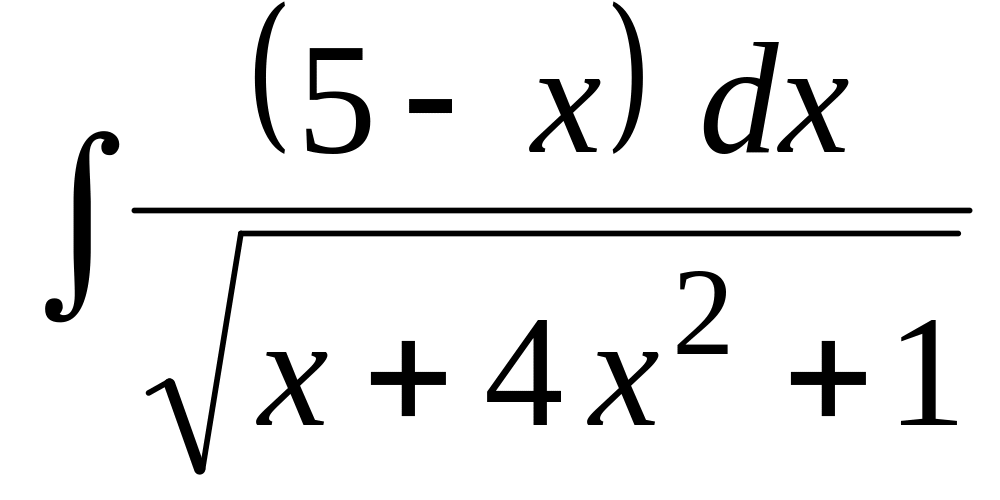 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
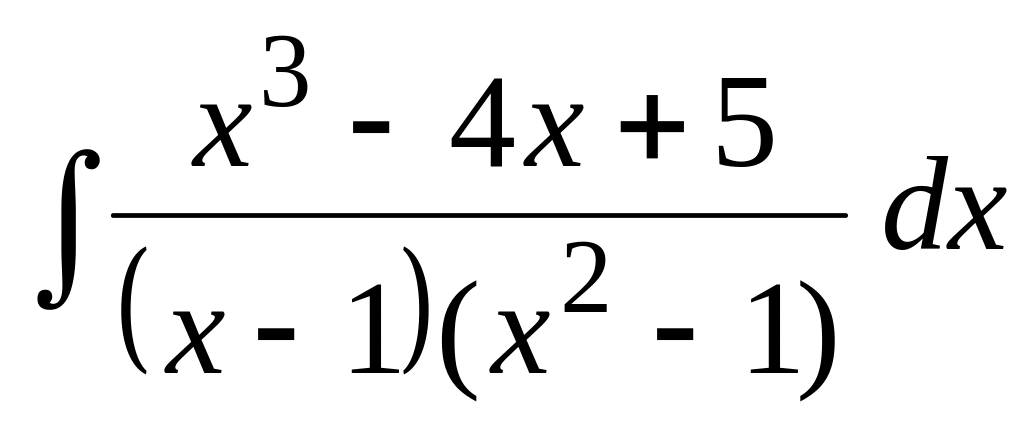 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
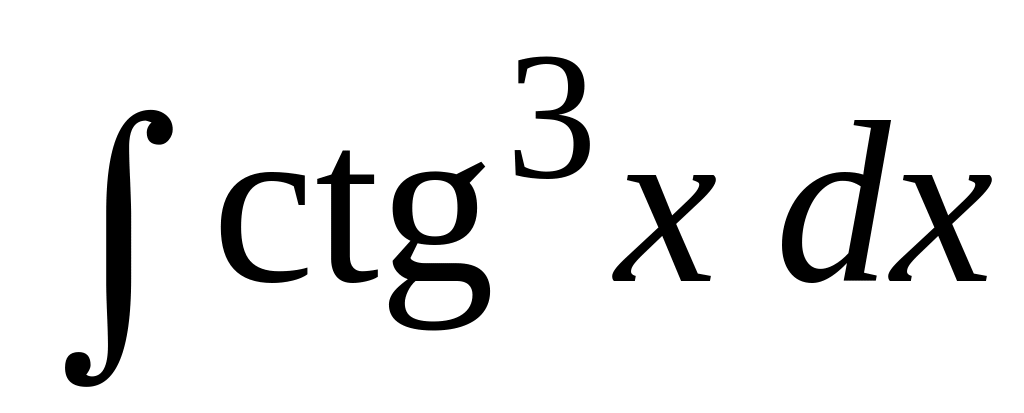 .
.Используя тригонометрические подстановки, найти интеграл:
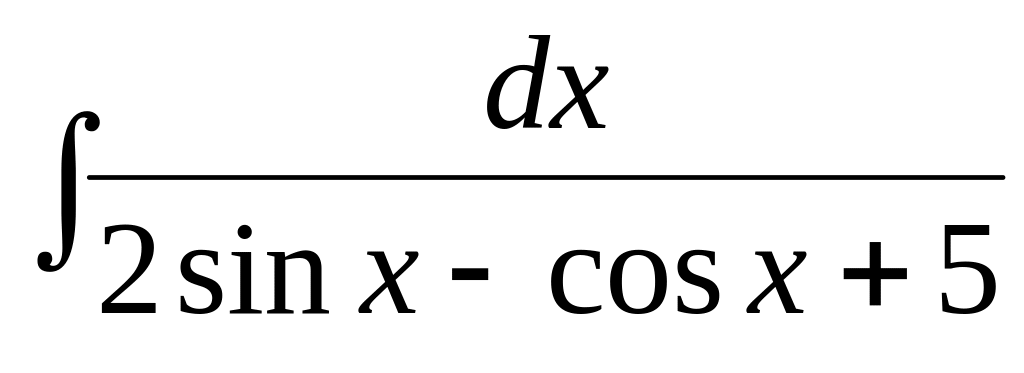 .
.
Вариант 21
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() .
1.2.
.
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
;
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]() ;
;
Найти неопределенный интеграл:
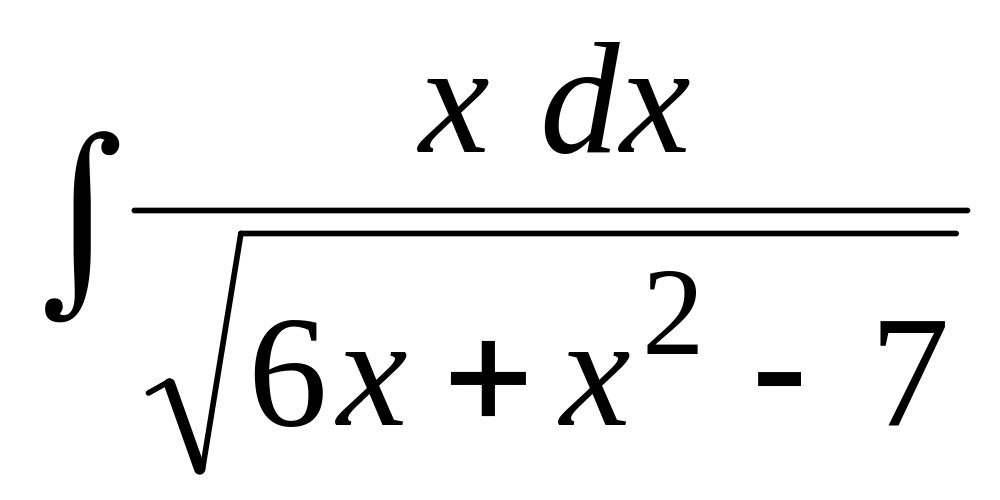 .
.Применяя метод неопределенных коэффициентов, найти интеграл: .
Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
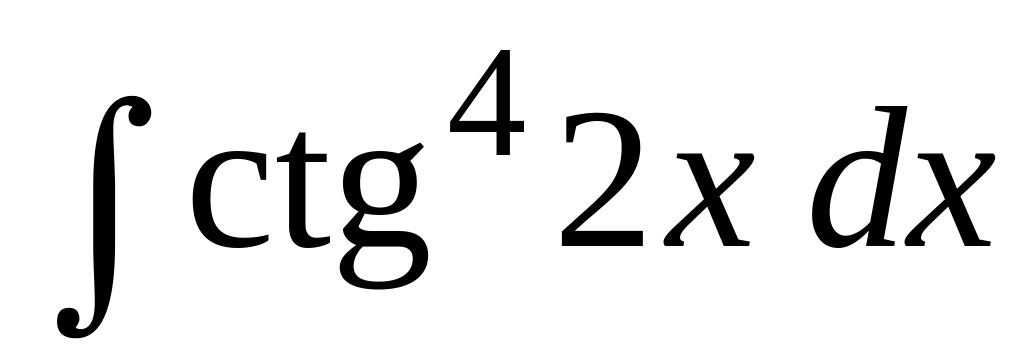 .
.Используя тригонометрические подстановки, найти интеграл:
 .
.
Вариант 22
Применяя подходящие подстановки, найти следующие интегралы:
1.1.![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() .
.
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]() .
.
Найти неопределенный интеграл:
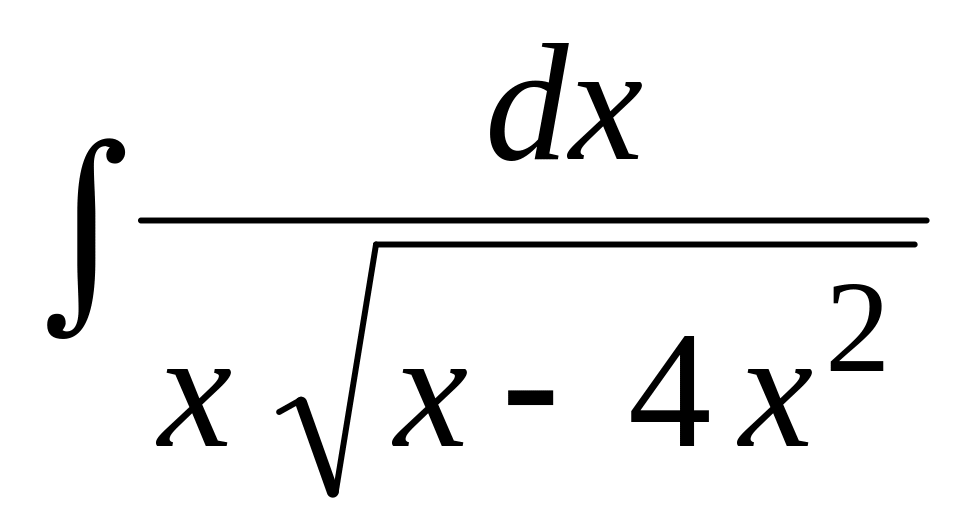 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
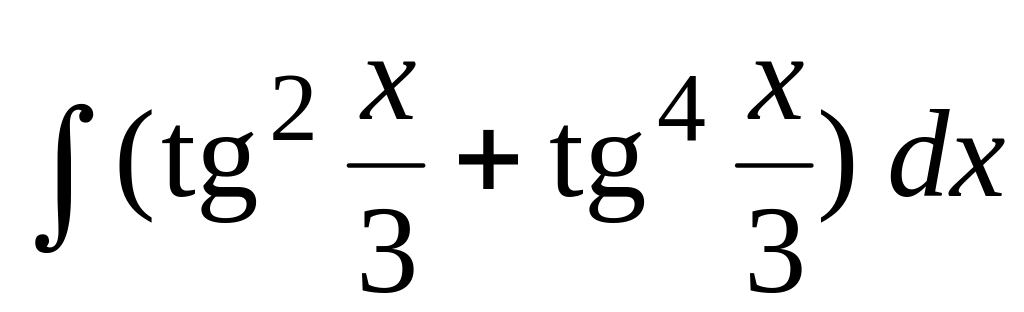 .
.Используя тригонометрические подстановки, найти интеграл:
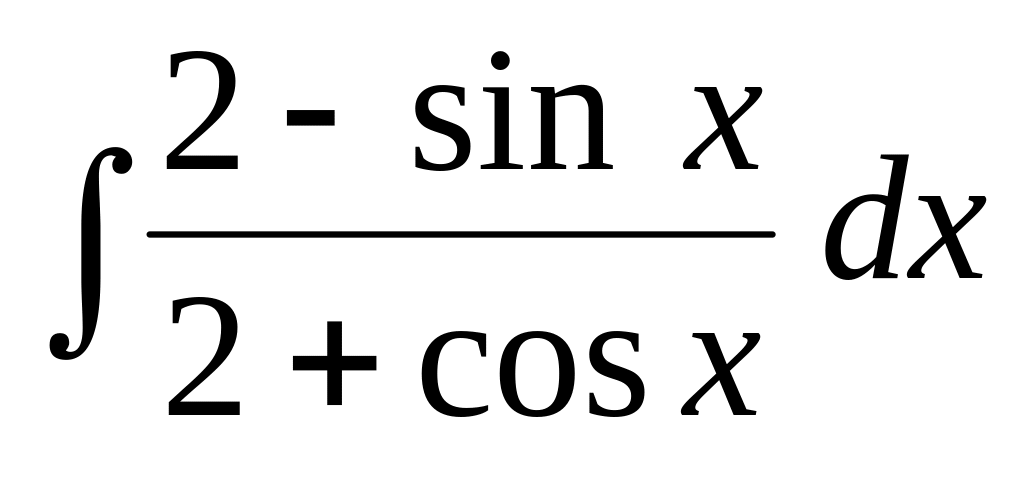 .
.
Вариант 23
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2
;
1.2![]() ;
1.3
;
1.3![]() .
.
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.![]() ;
2.3.
;
2.3.
![]() .
.
Найти неопределенный интеграл:
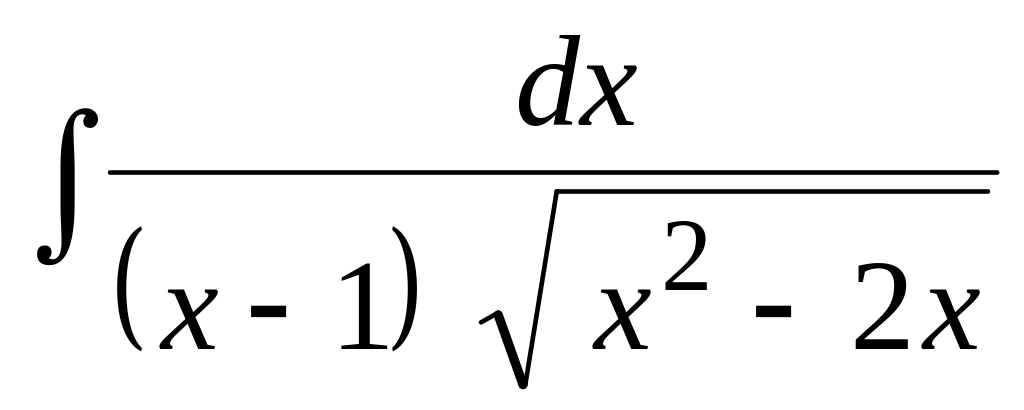 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
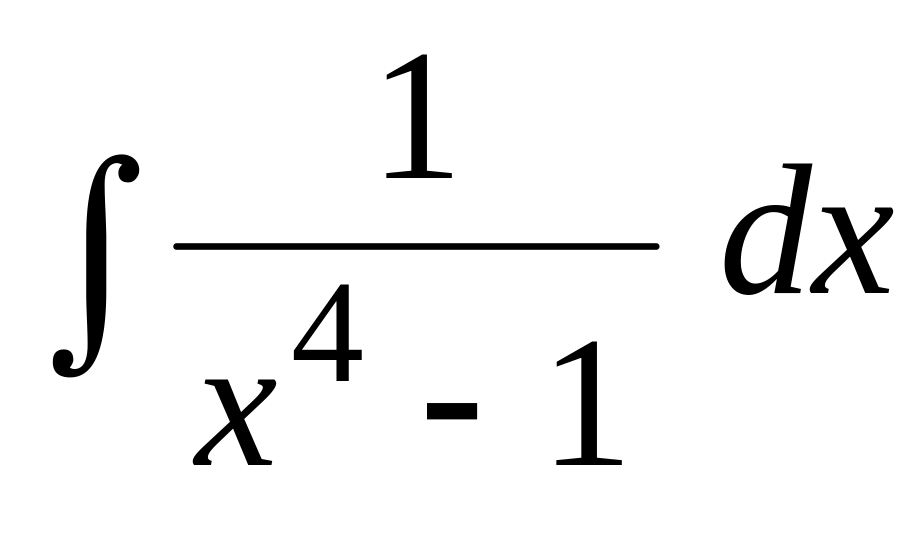 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]()
Вычислить интегралы от тригонометрических функций:
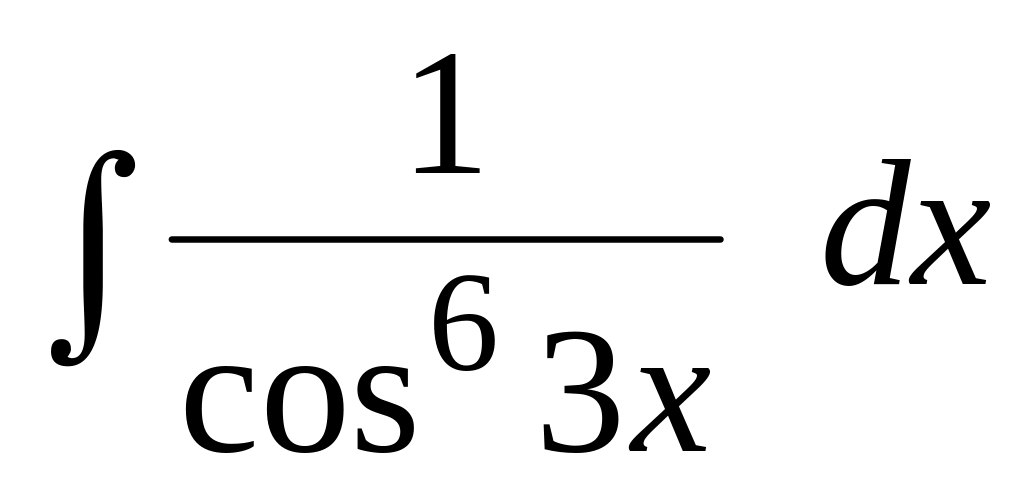 .
.Используя тригонометрические подстановки, найти интеграл: .
Вариант 24
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3
;
1.3![]() ;
;
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]()
Найти неопределенный интеграл:
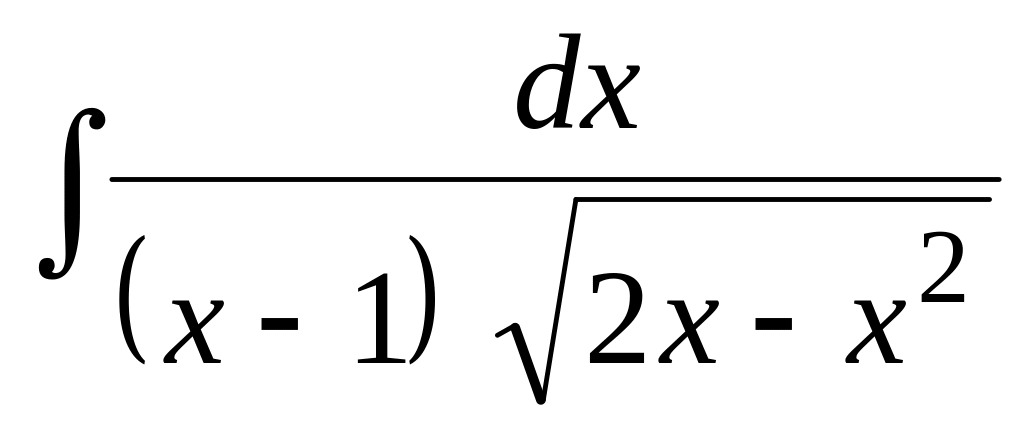 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
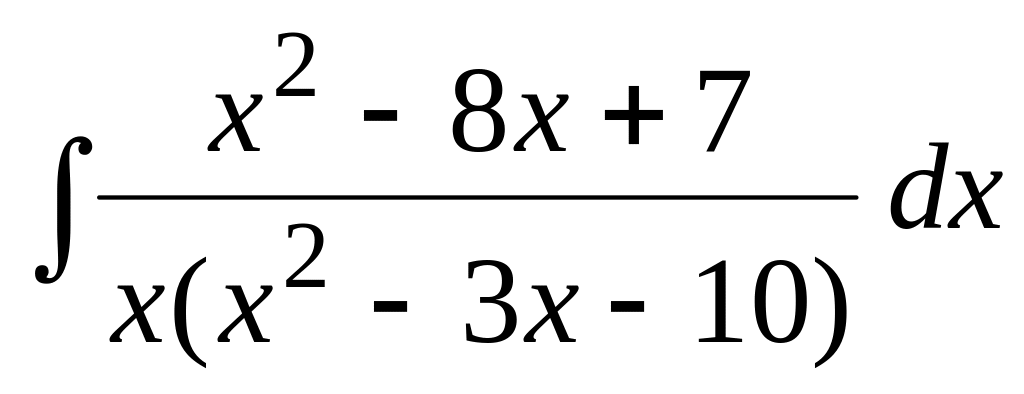 .
.Применяя тригонометрические подстановки, найти интеграл:
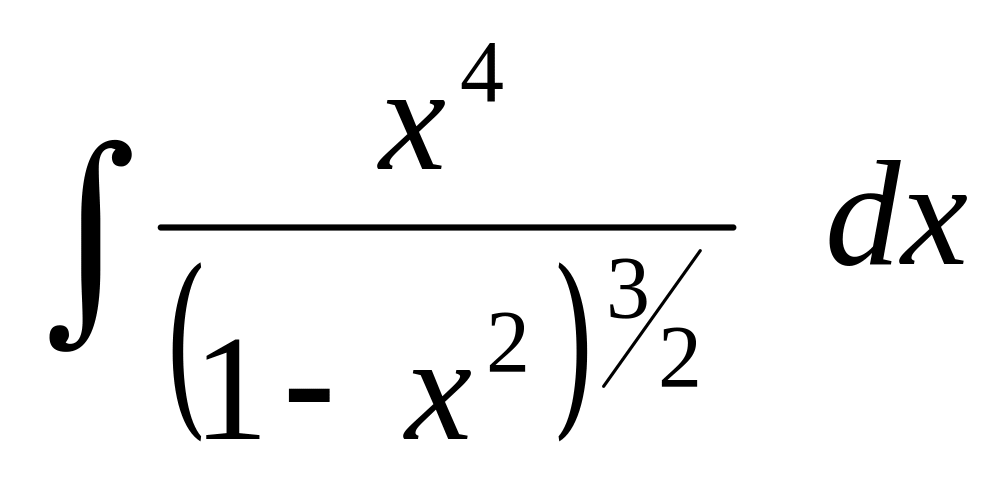
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
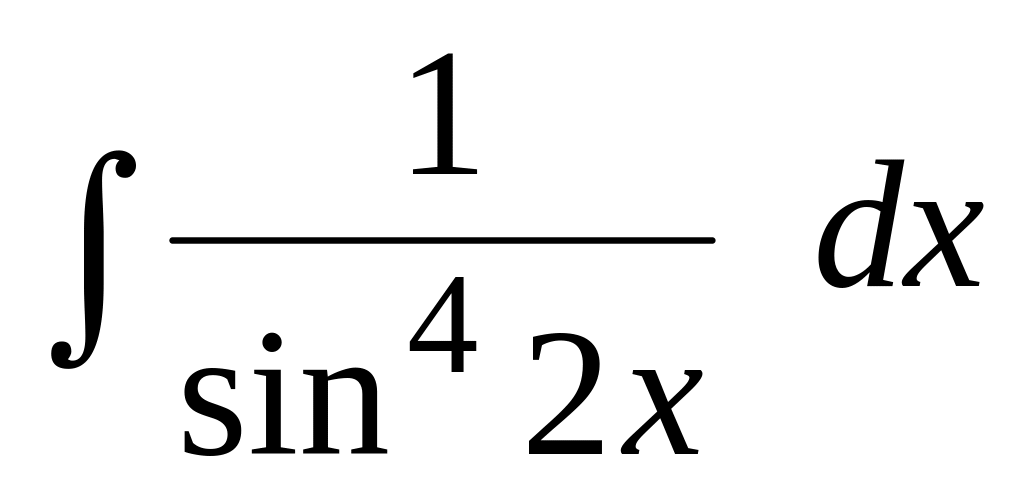 .
.Используя тригонометрические подстановки, найти интеграл:
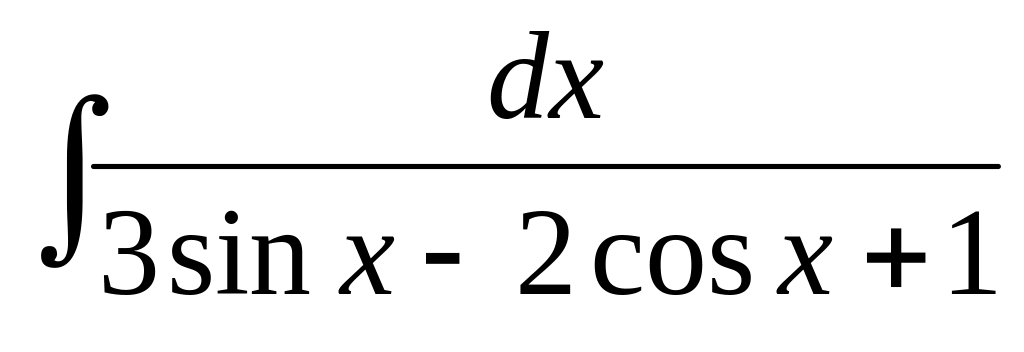 .
.
Вариант 25
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() .
1.2
.
1.2![]() ;
1.3.
;
1.3.![]()
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2
;
2.2![]() ;
2.3.
;
2.3.
![]() ;
;
Найти неопределенный интеграл:
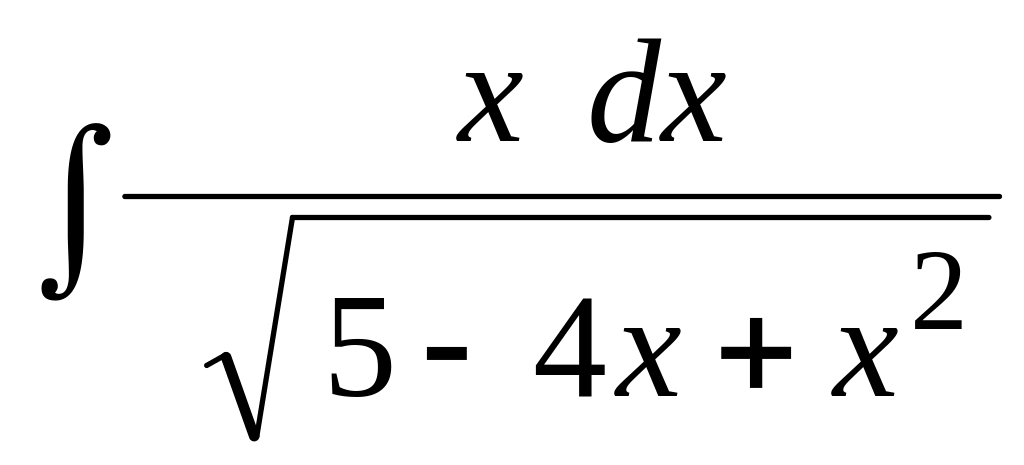 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
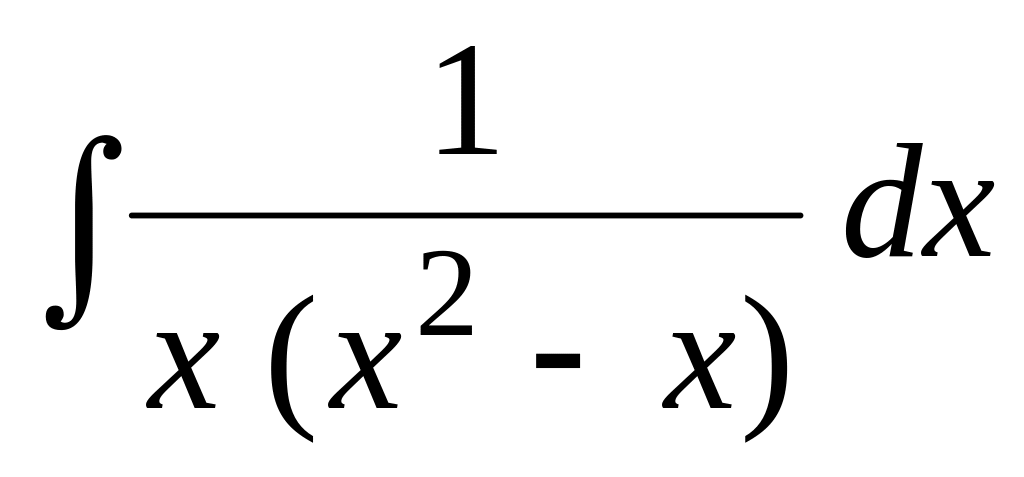 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
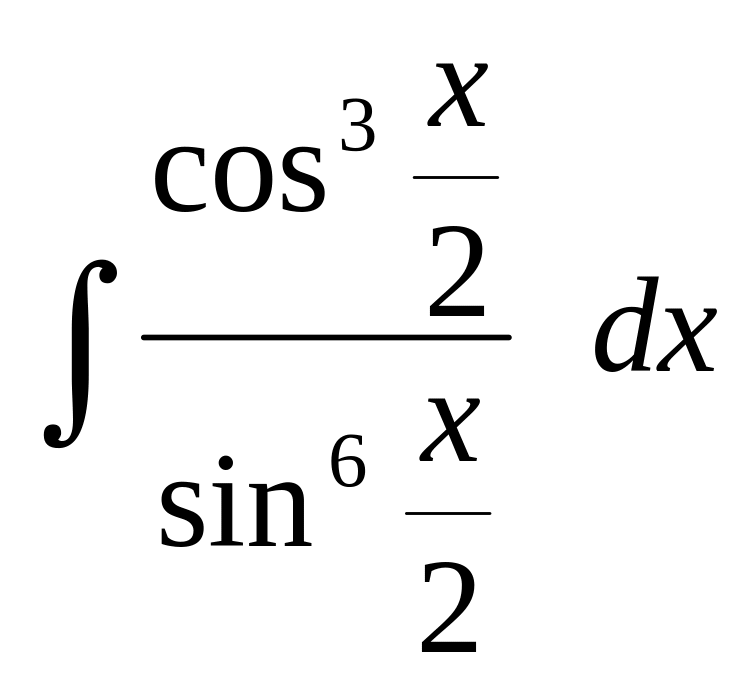 .
.Используя тригонометрические подстановки, найти интеграл:
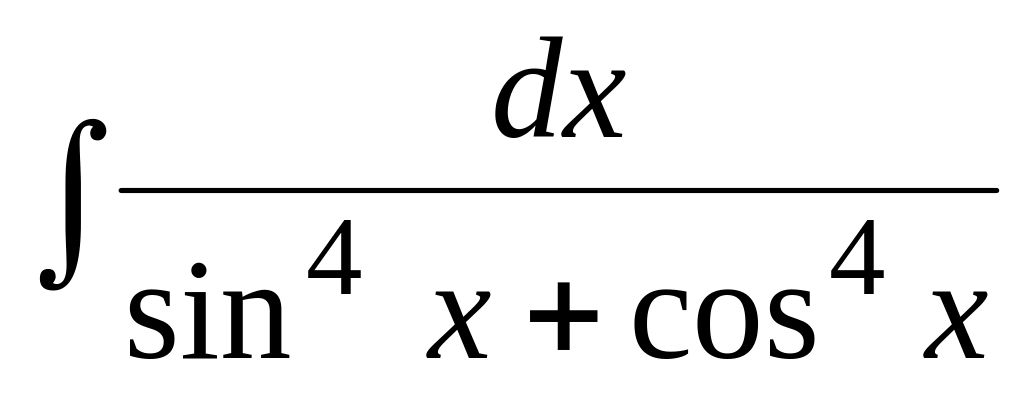 .
.
Вариант 26
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
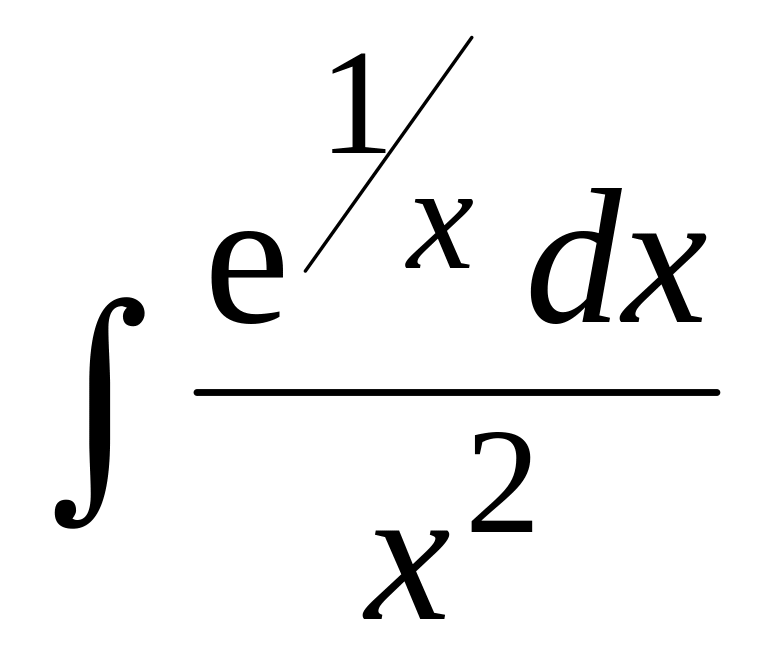 ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
;
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]() ;
;
Найти неопределенный интеграл:
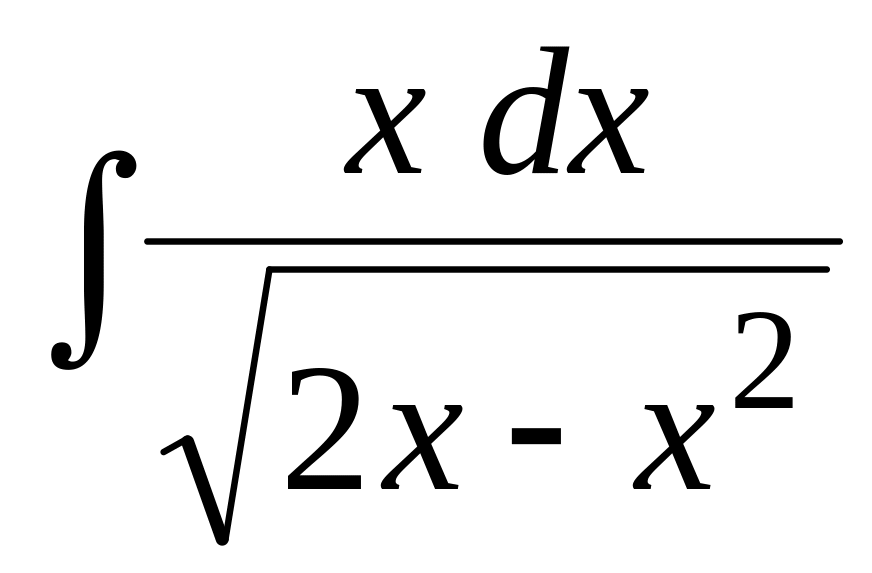 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
 .
.Применяя тригонометрические подстановки, найти интеграл:
![]()
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
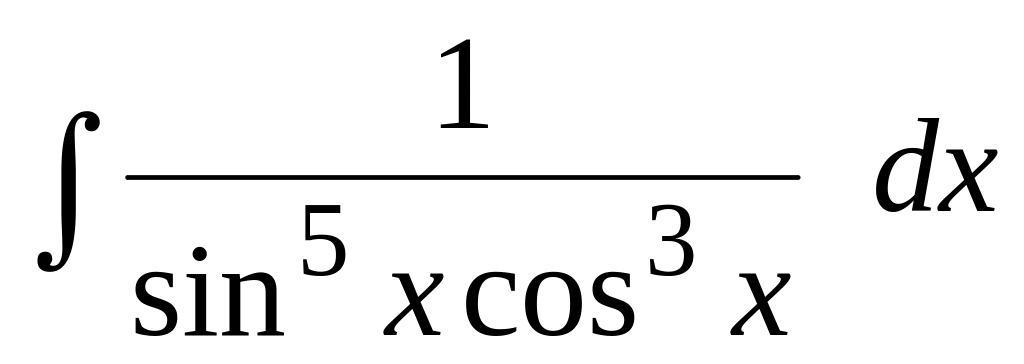 .
.Используя тригонометрические подстановки, найти интеграл:
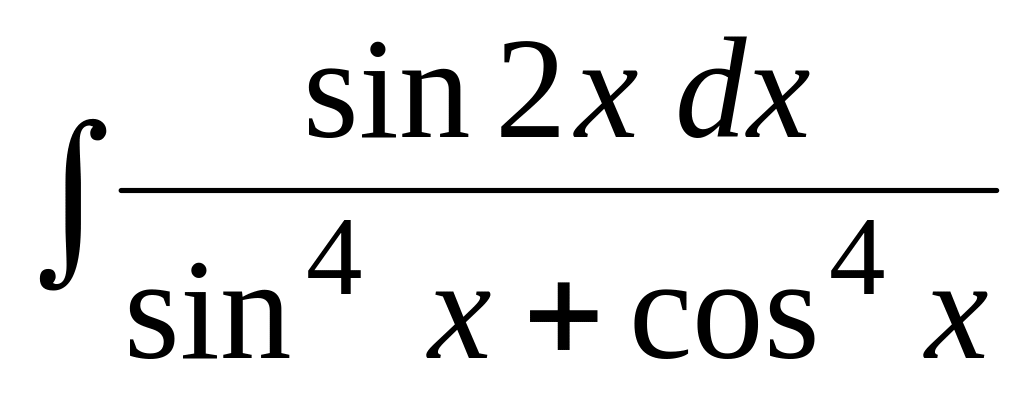 .
.
Вариант 27
Применяя подходящие подстановки, найти следующие интегралы:
1.1.![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
;
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.![]() ;
2.3.
;
2.3.
![]() ;
;
Найти неопределенный интеграл:
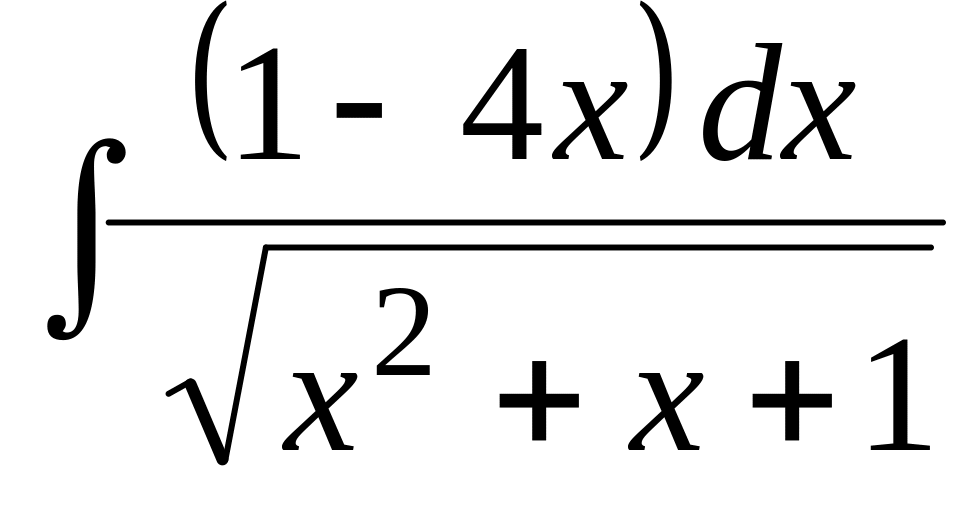 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
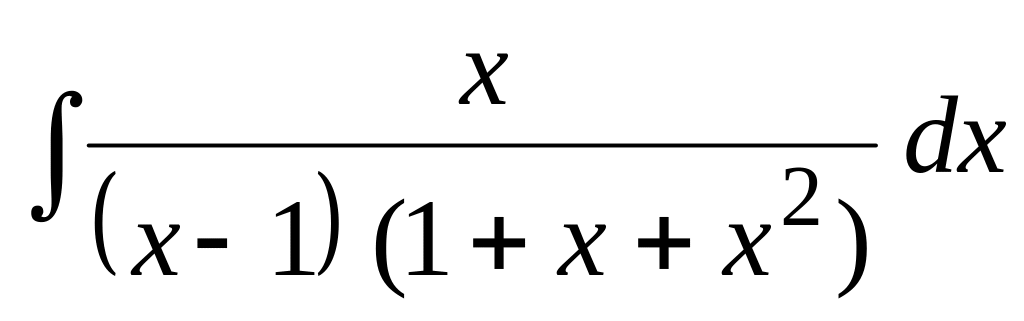 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
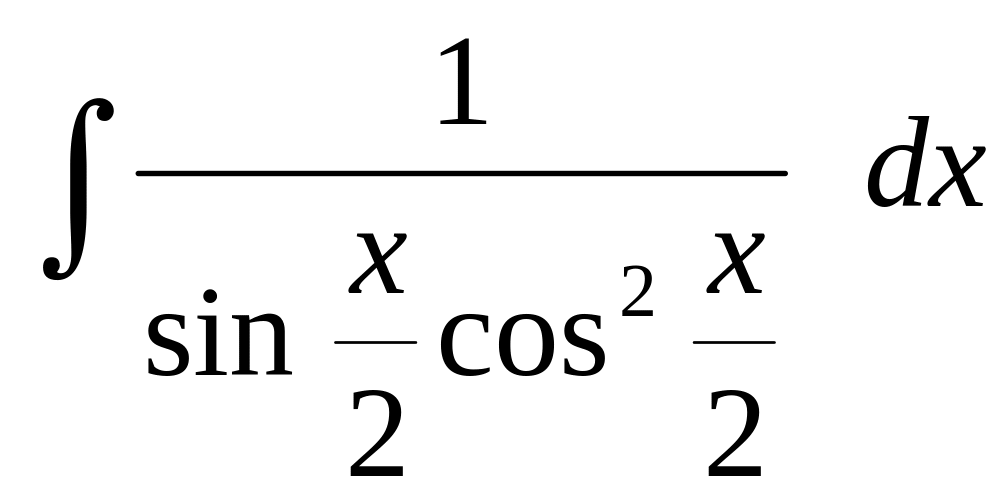
Используя тригонометрические подстановки, найти интеграл:
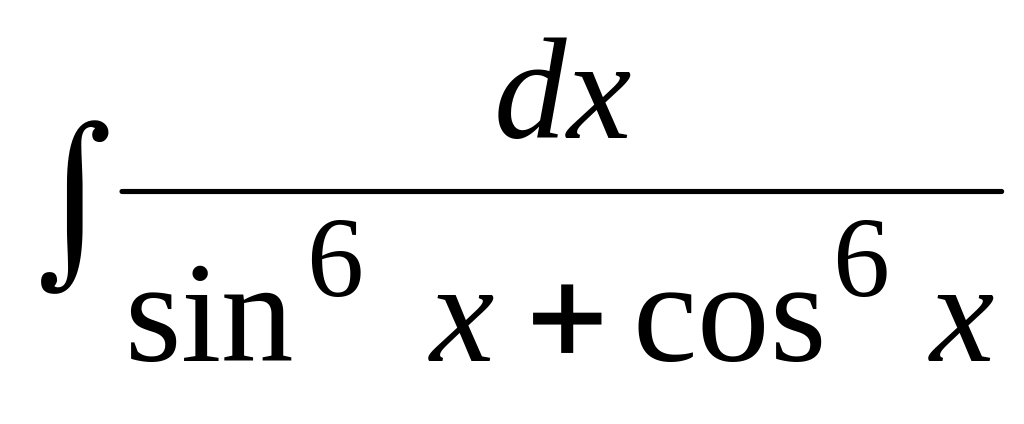 .
.
Вариант 28
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() ;
;
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.![]() ;
2.2
;
2.2![]() ;
2.3.
;
2.3.
![]() ;
;
Найти неопределенный интеграл:
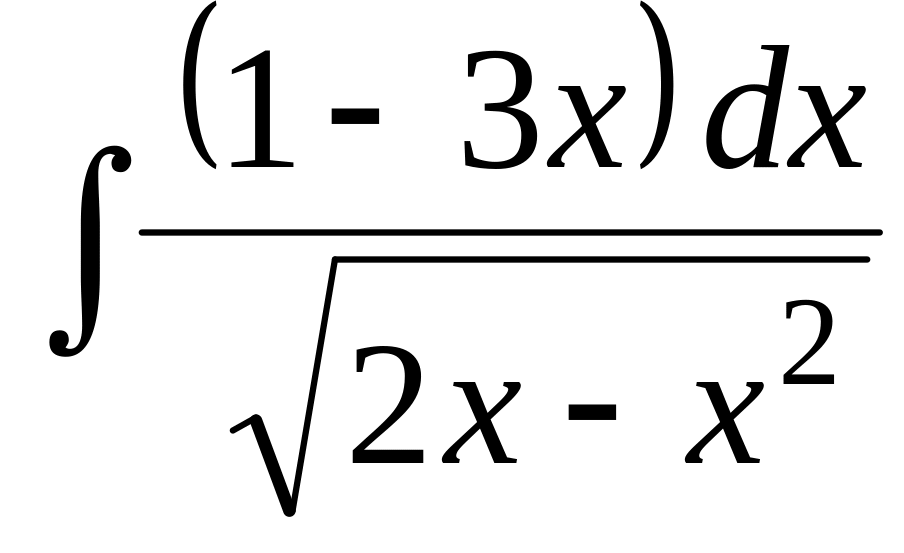 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
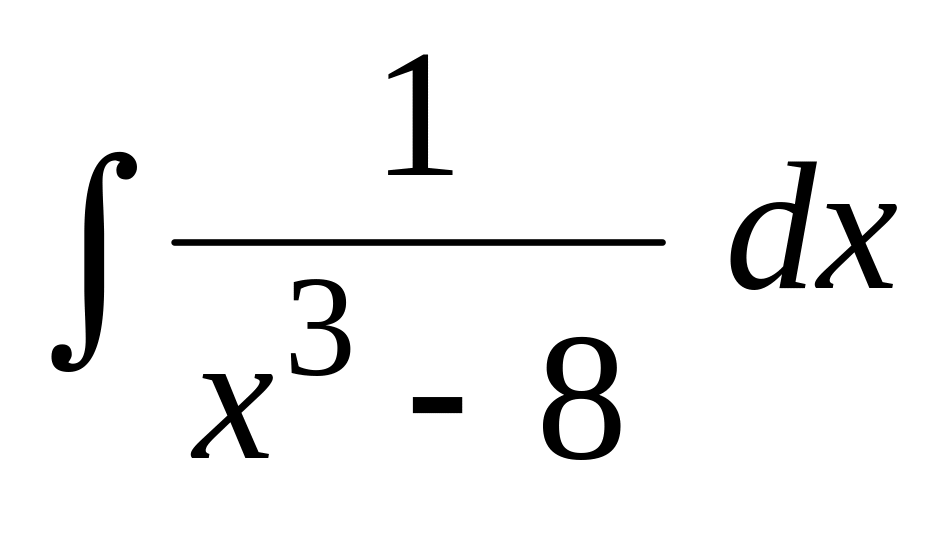 .
.Применяя тригонометрические подстановки, найти интеграл:
![]() .
.
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
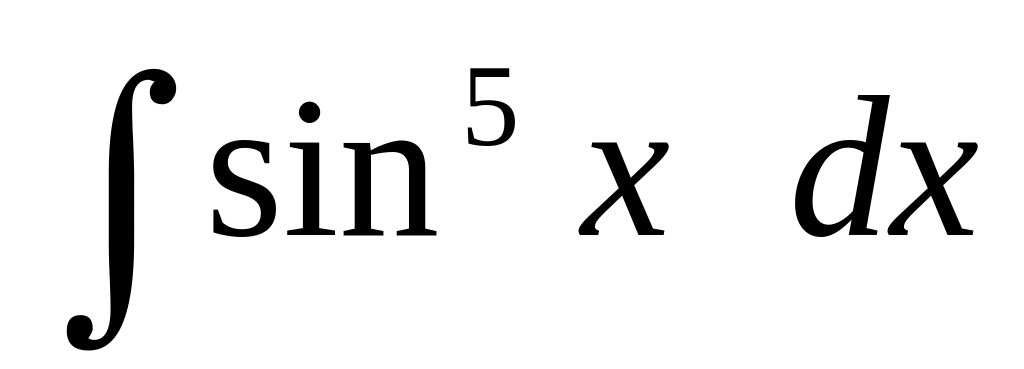
Используя тригонометрические подстановки, найти интеграл:
 .
.
Вариант 29
Применяя подходящие подстановки, найти следующие интегралы:
1.1![]() ;1.2.
;1.2.
![]() ;
1.3.
;
1.3.
![]()
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() .;
2.3.
.;
2.3.
![]()
Найти неопределенный интеграл:
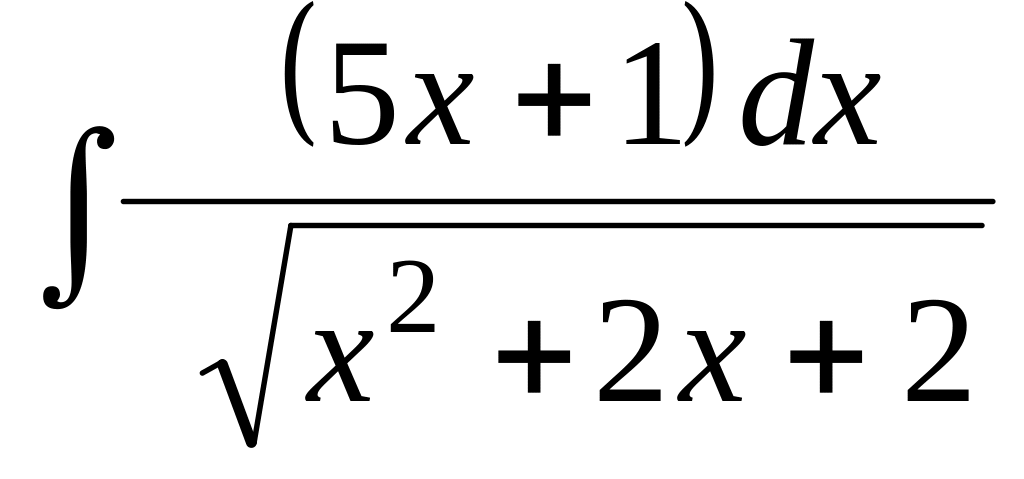 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
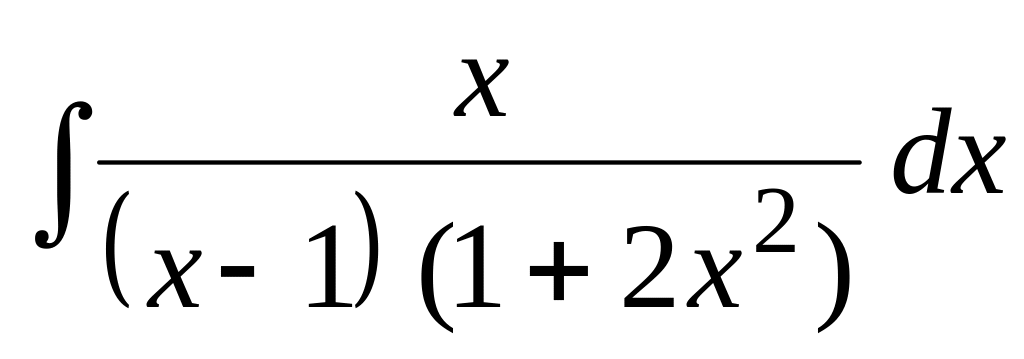 .
.Применяя тригонометрические подстановки, найти интеграл:
![]()
Вычислить интеграл от иррациональных функций:
.
Вычислить интегралы от тригонометрических функций:
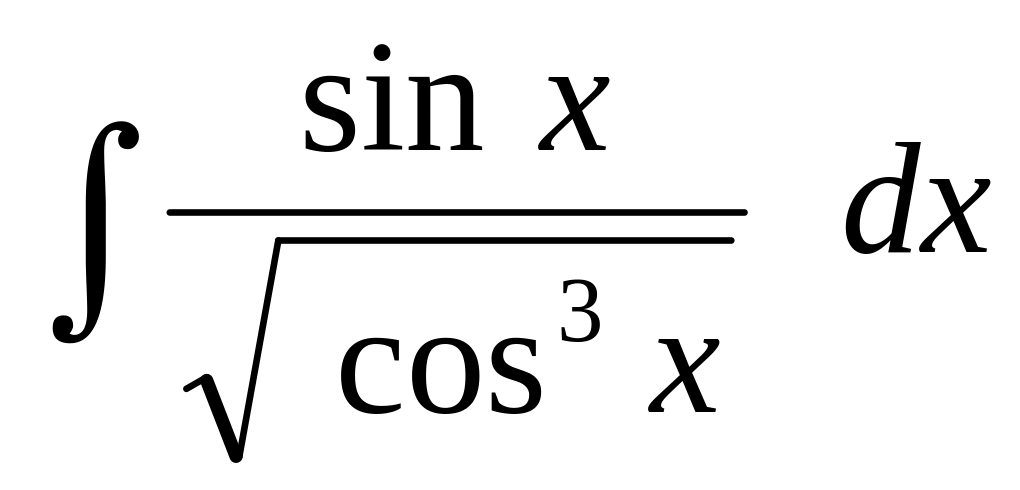
Используя тригонометрические подстановки, найти интеграл:
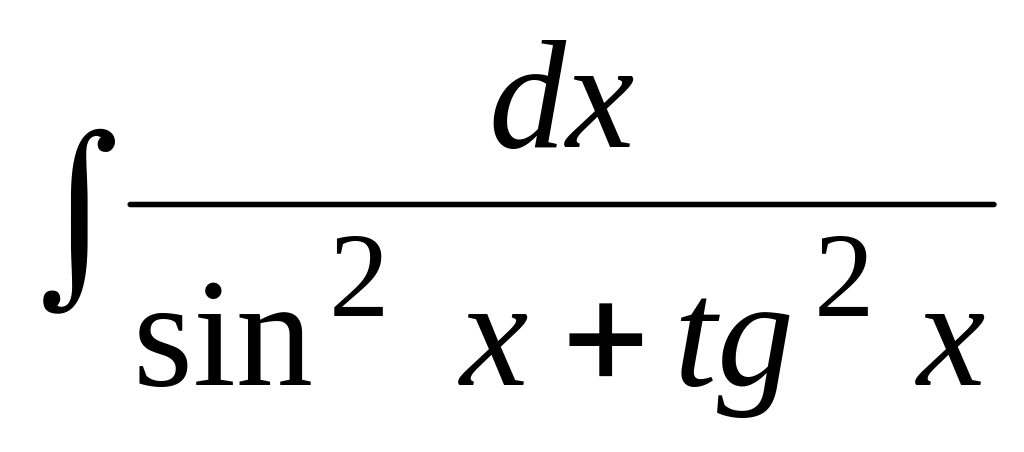 .
.
Вариант 30
Применяя подходящие подстановки, найти следующие интегралы:
1.1.
![]() ;
1.2.
;
1.2.
![]() ;
1.3.
;
1.3.
![]() .
.
Применяя метод интегрирования по частям, найти следующие интегралы:
2.1.
![]() ;
2.2.
;
2.2.
![]() ;
2.3.
;
2.3.
![]() .
.
Найти неопределенный интеграл:
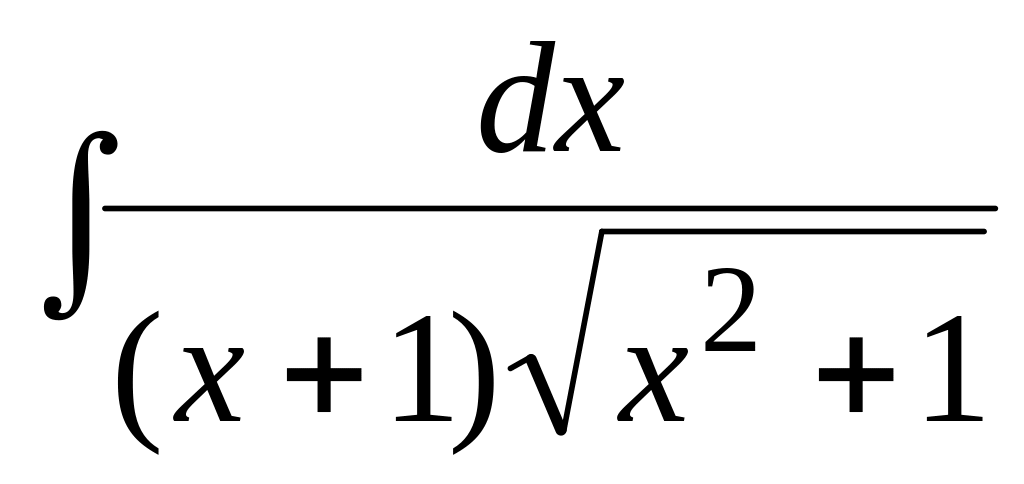 .
.Применяя метод неопределенных коэффициентов, найти интеграл:
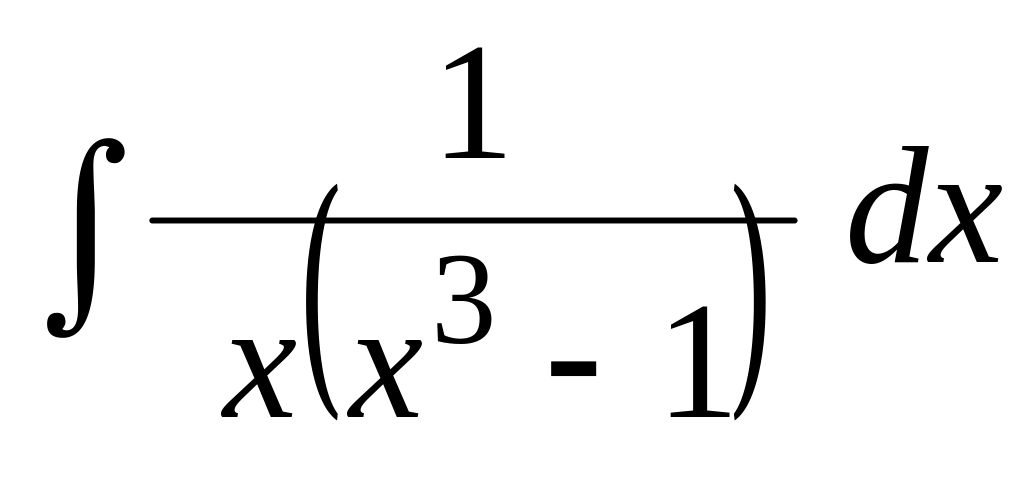
Применяя тригонометрические подстановки, найти интеграл:
![]()
Вычислить интеграл от иррациональных функций:
![]() .
.
Вычислить интегралы от тригонометрических функций:
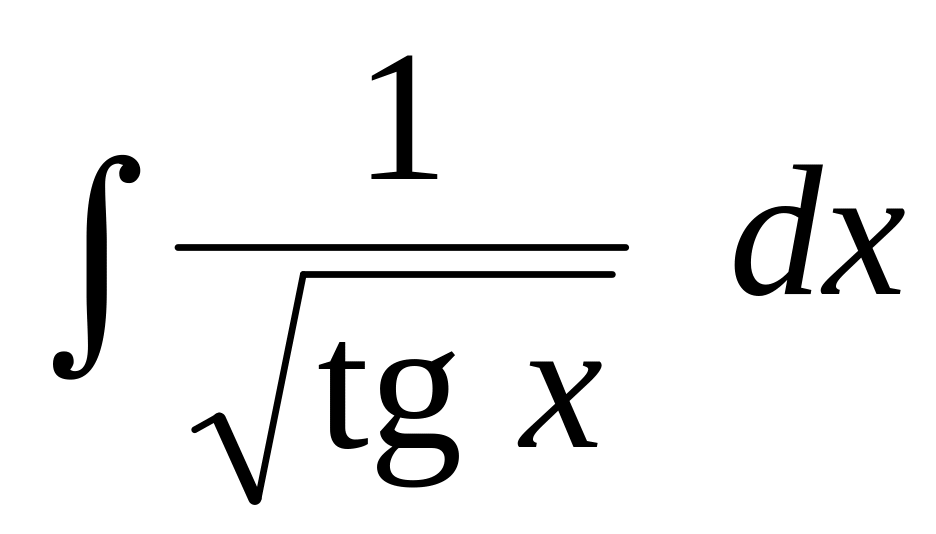 .
.Используя тригонометрические подстановки, найти интеграл:
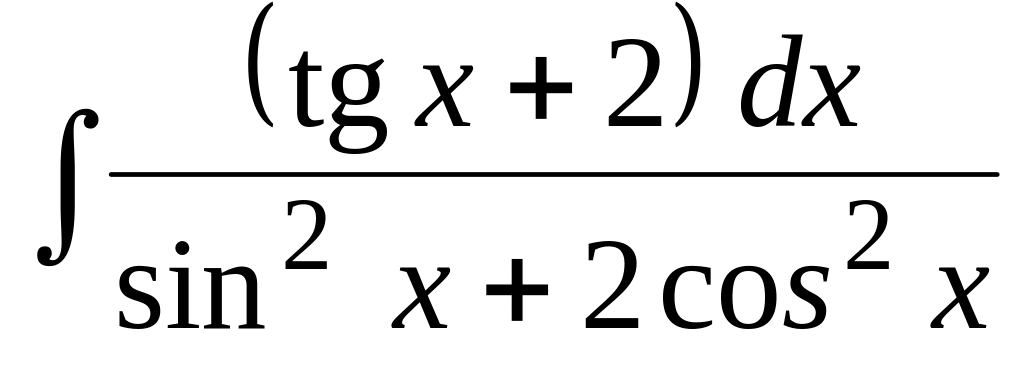 .
.
