Варианты заданий.

Вариант 1

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ; 1.2. ; 1.3.

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. ; 2.3. .

3. Найти неопределенный интеграл: .

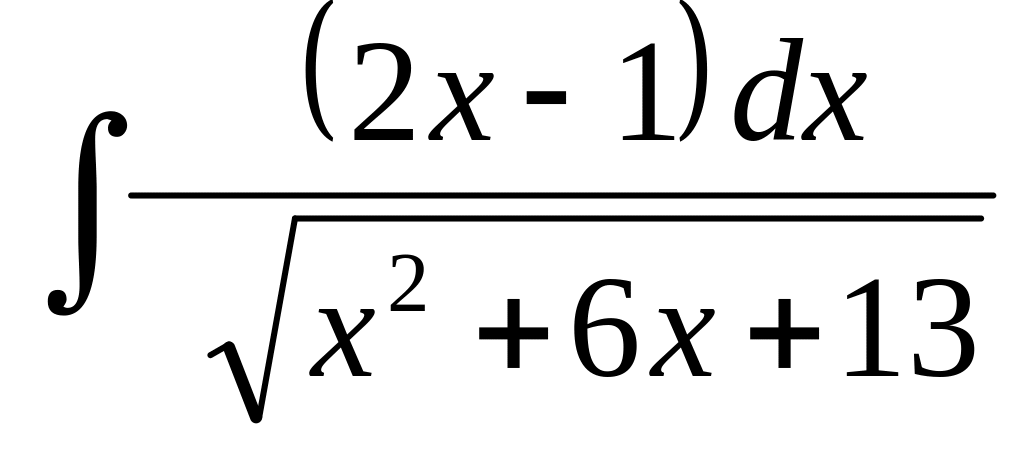4. Применяя метод неопределенных коэффициентов, найти интеграл: .

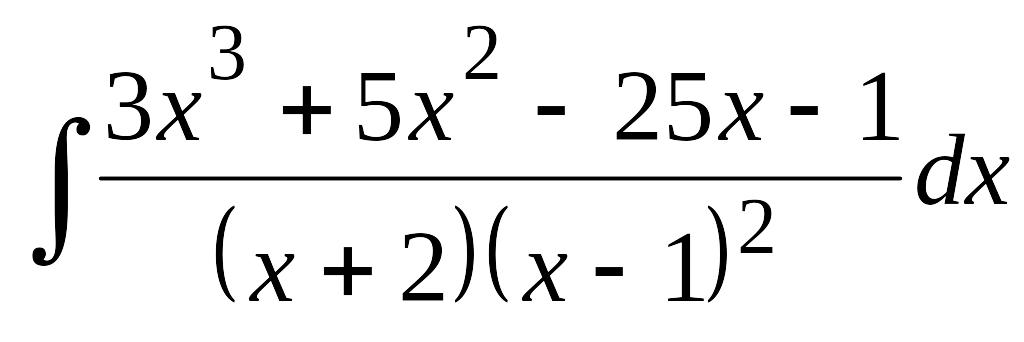5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

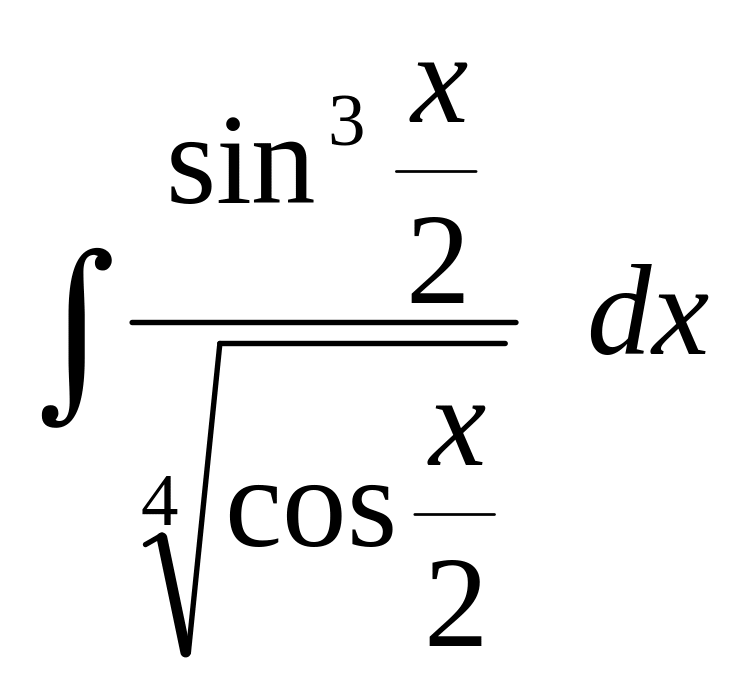   2. Используя тригонометрические подстановки, найти интеграл: .

Вариант 2

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ; 1.2. ; 1.3. .

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. ; 2.3. ;

3. Найти неопределенный интеграл: .

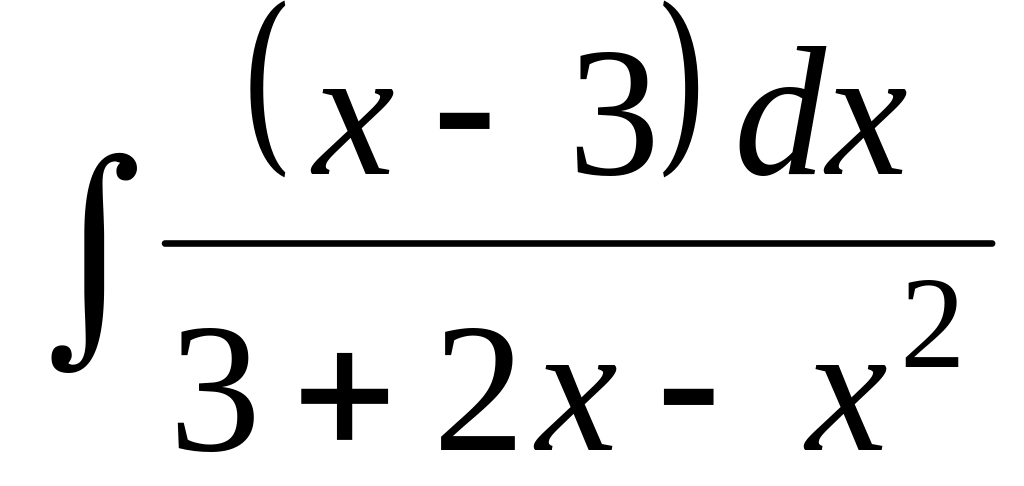4. Применяя метод неопределенных коэффициентов, найти интеграл: .

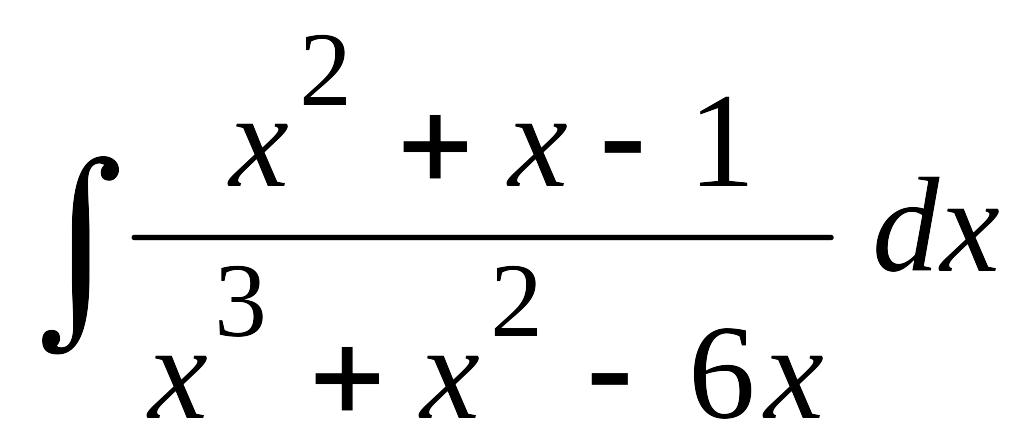5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

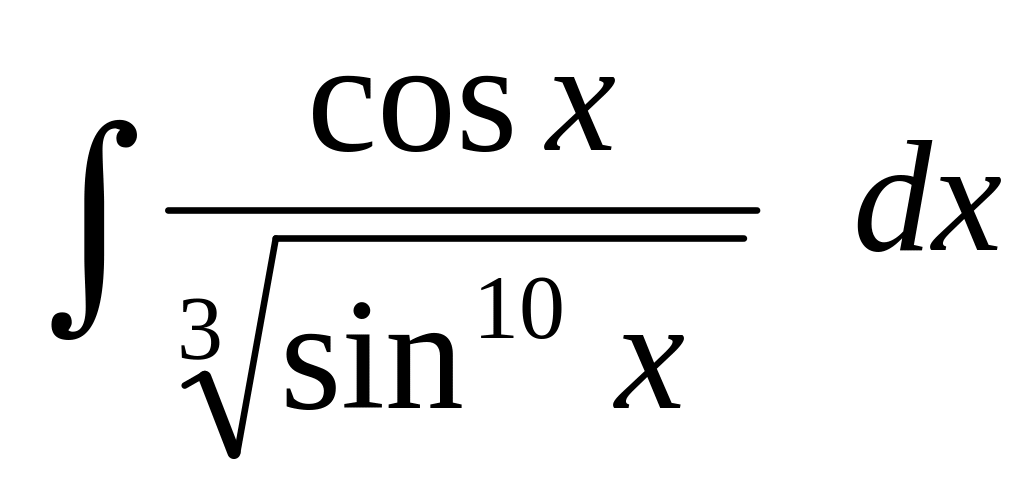   2. Используя тригонометрические подстановки, найти интеграл: .

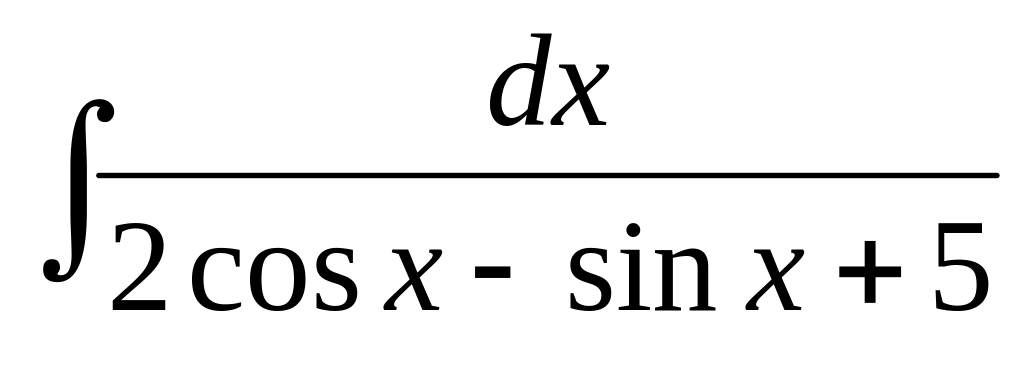Вариант 3

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ;1.2. ; 1.3. ;

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. 2.2 ; 3.1. ;

3. Найти неопределенный интеграл: .

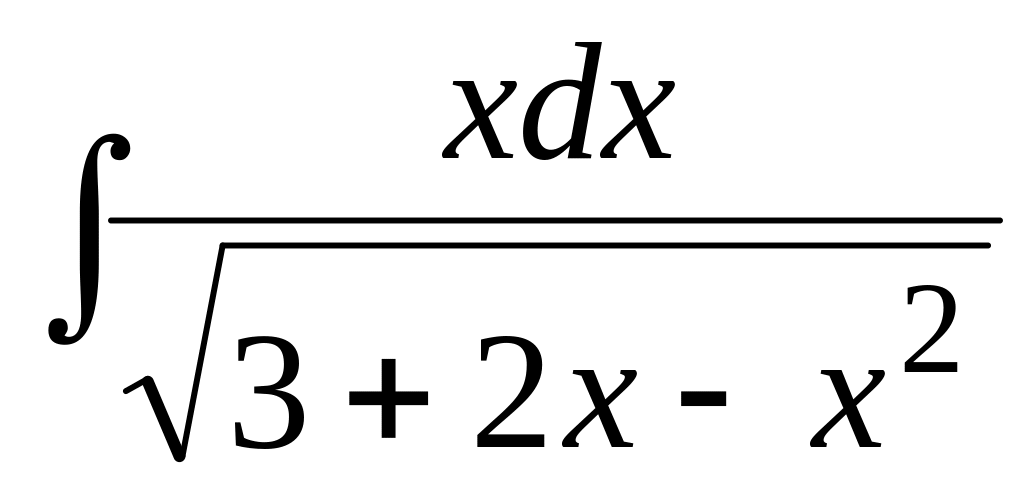4. Применяя метод неопределенных коэффициентов, найти интеграл: .

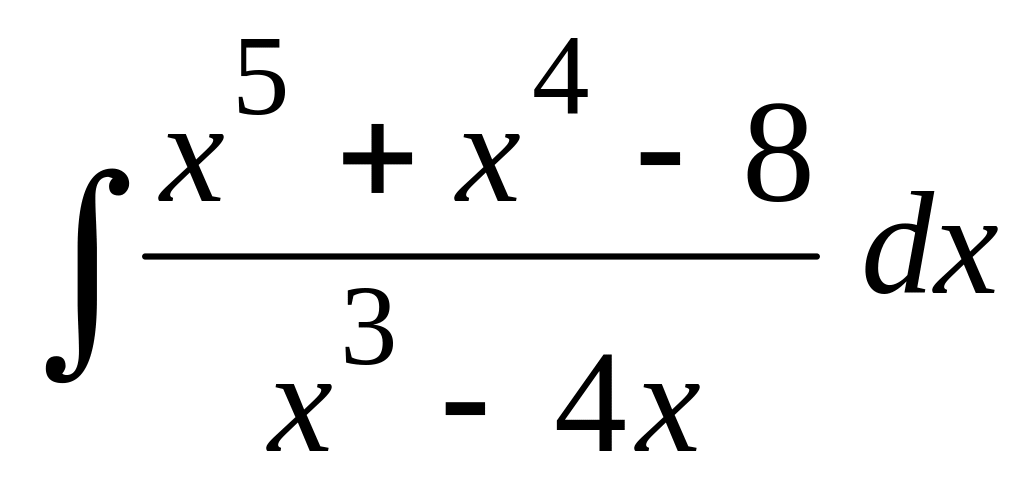5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

   2. Используя тригонометрические подстановки, найти интеграл: .

Вариант 4

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ; 1.2. ; 1.3. ;

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. ; 2.3. ;

3. Найти неопределенный интеграл: .

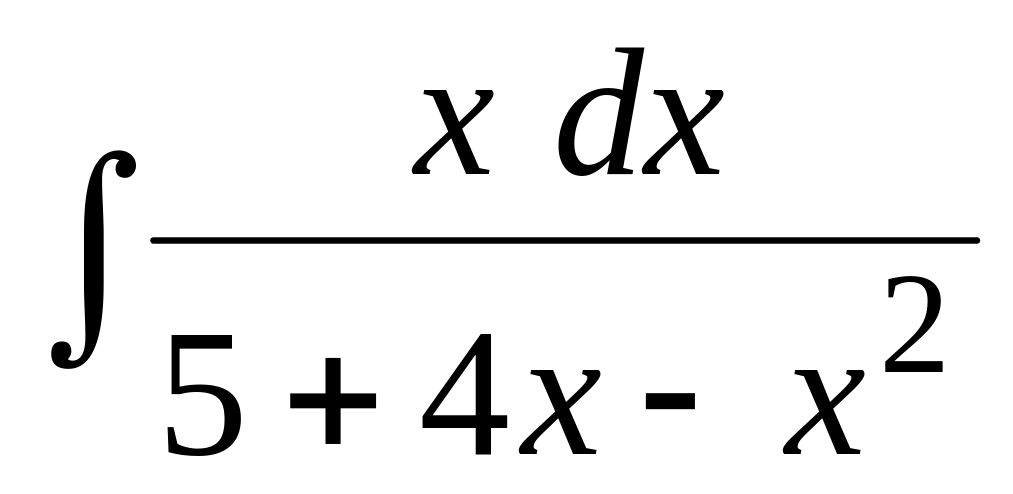4. Применяя метод неопределенных коэффициентов, найти интеграл: .

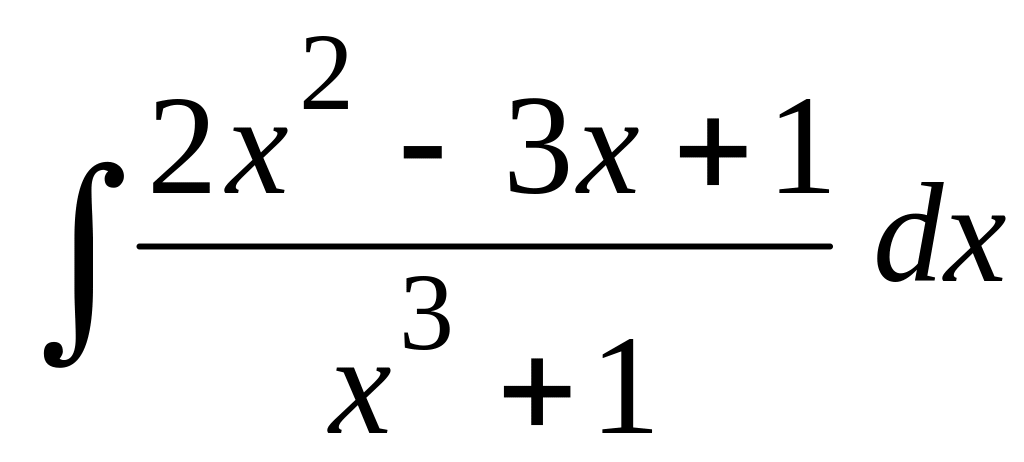5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

   2. Используя тригонометрические подстановки, найти интеграл: .

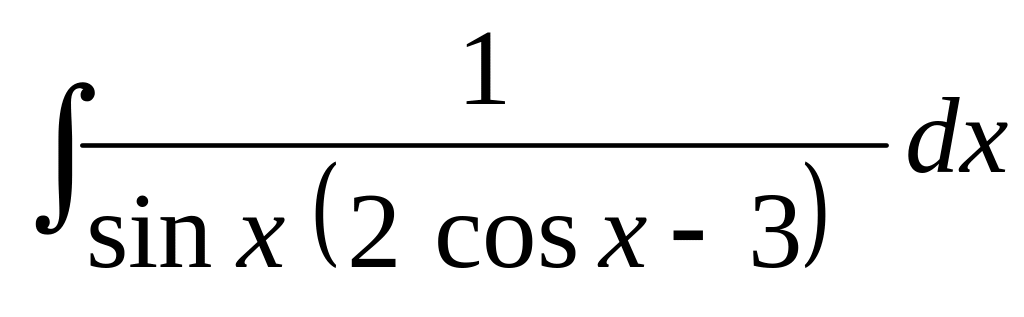Вариант 5

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1 ; 1.2. ; 1.3. .

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. . 2.3. ;

3. Найти неопределенный интеграл: .

4. Применяя метод неопределенных коэффициентов, найти интеграл:

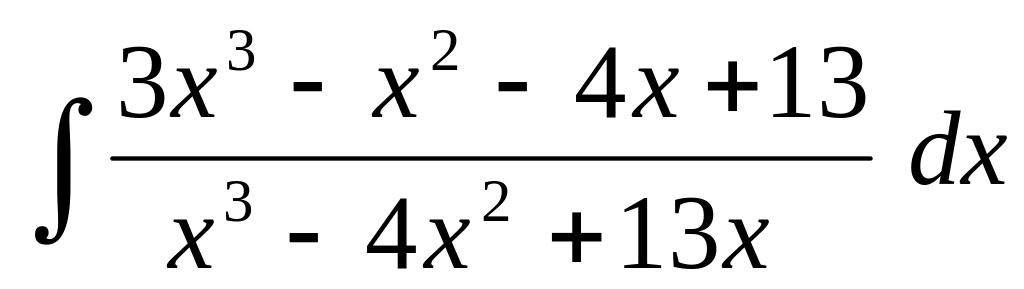
5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

   2. Используя тригонометрические подстановки, найти интеграл:

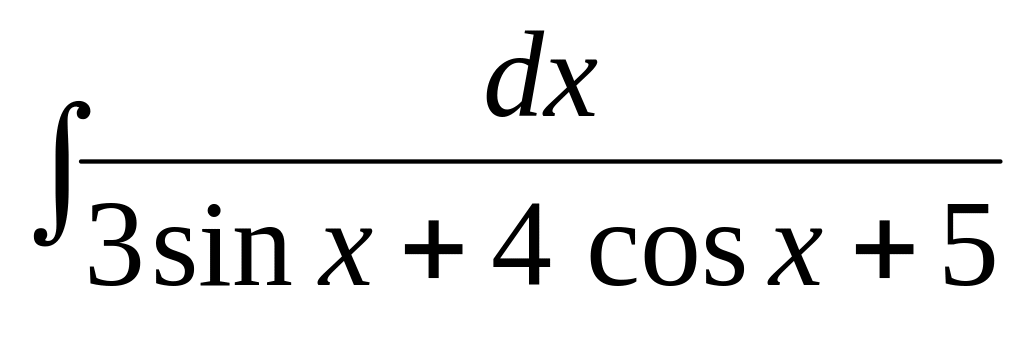
Вариант 6

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ; 1.2. ; 1.3. ;

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. ; 2.3. ;

3. Найти неопределенный интеграл: .

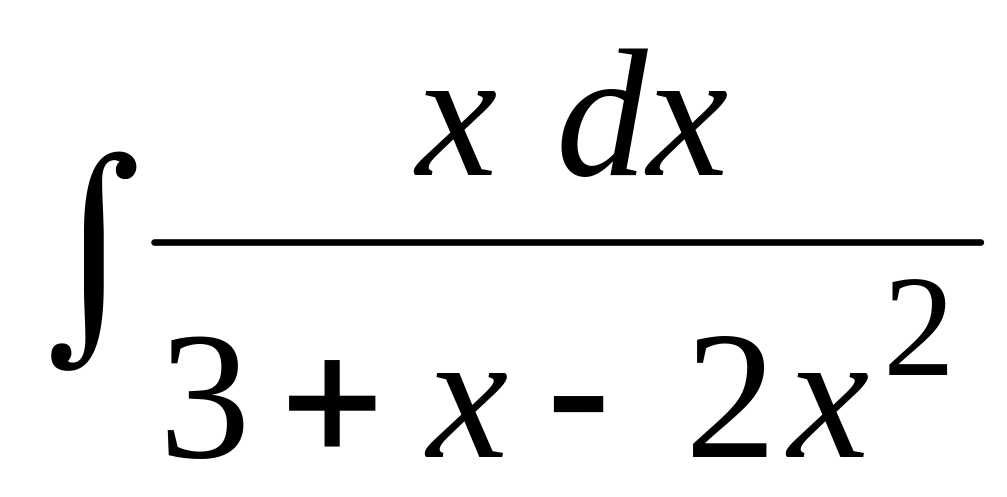4. Применяя метод неопределенных коэффициентов, найти интеграл: .

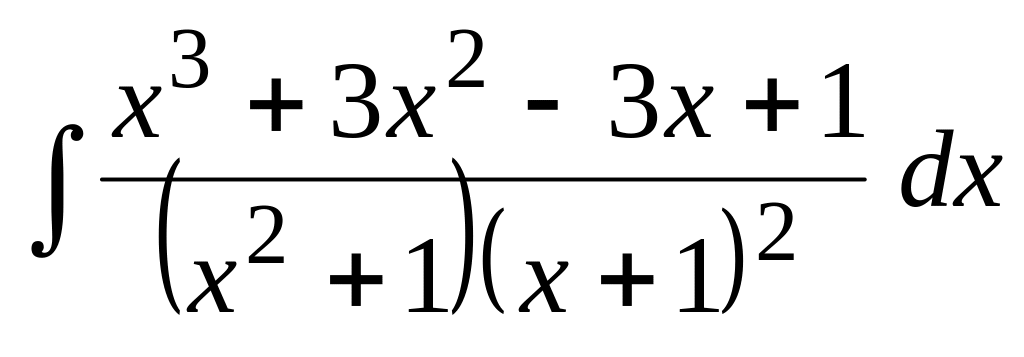5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

   2. Используя тригонометрические подстановки, найти интеграл: .

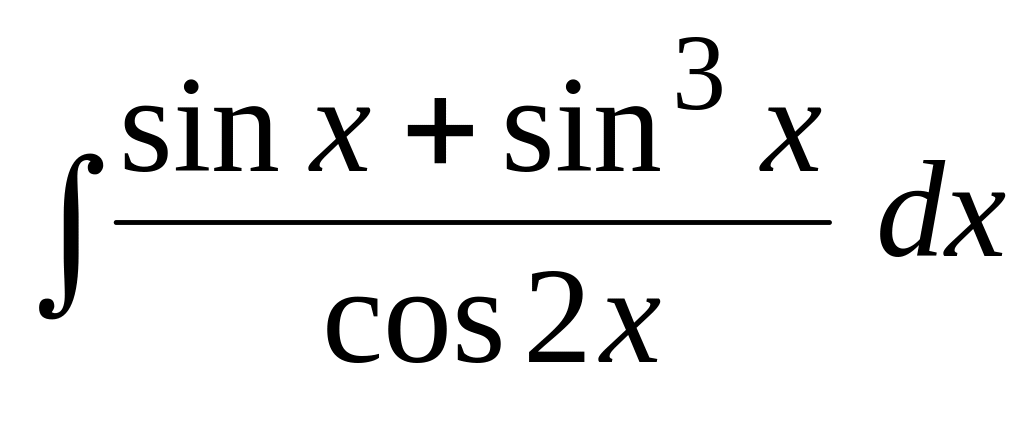Вариант 7

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ; 1.2. ; 1.3. .

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. ; 2.3.

3. Найти неопределенный интеграл: .

4. Применяя метод неопределенных коэффициентов, найти интеграл: .

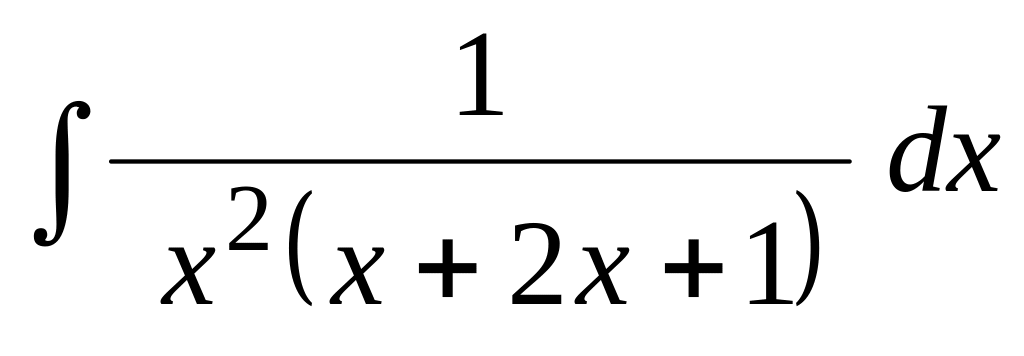5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

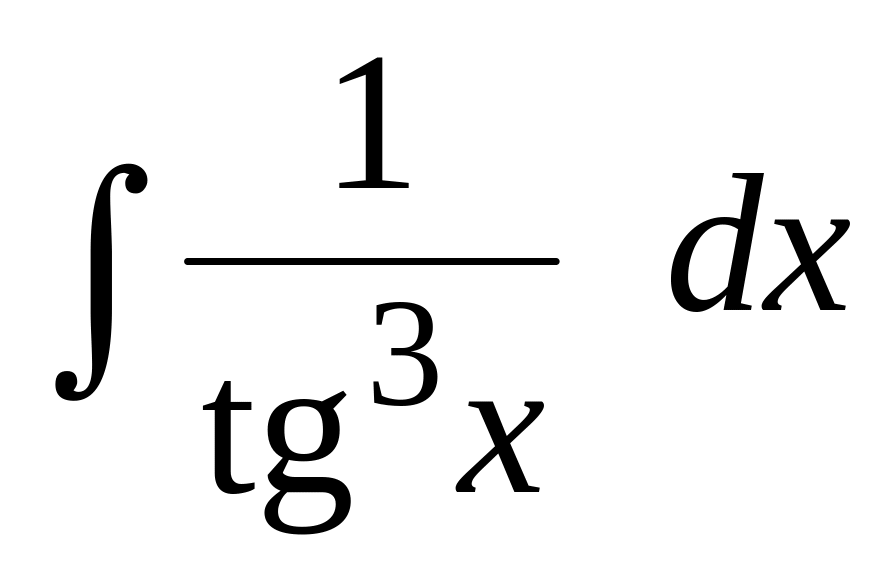   2. Используя тригонометрические подстановки, найти интеграл: .

Вариант 8

1. Применяя подходящие подстановки, найти следующие интегралы:

1.1. ; 1.2. ; 1.3. .

2. Применяя метод интегрирования по частям, найти следующие интегралы:

2.1. ; 2.2. ; 2.3. .

3. Найти неопределенный интеграл: .

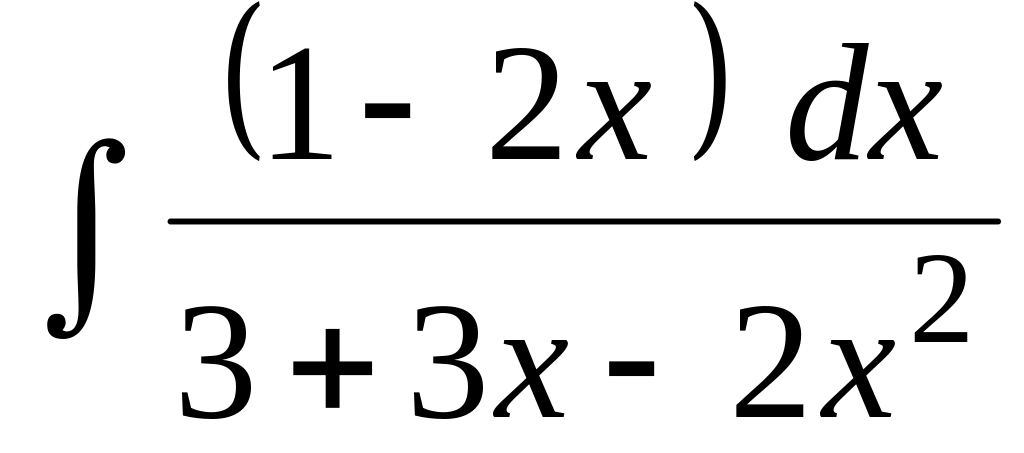4. Применяя метод неопределенных коэффициентов, найти интеграл: .

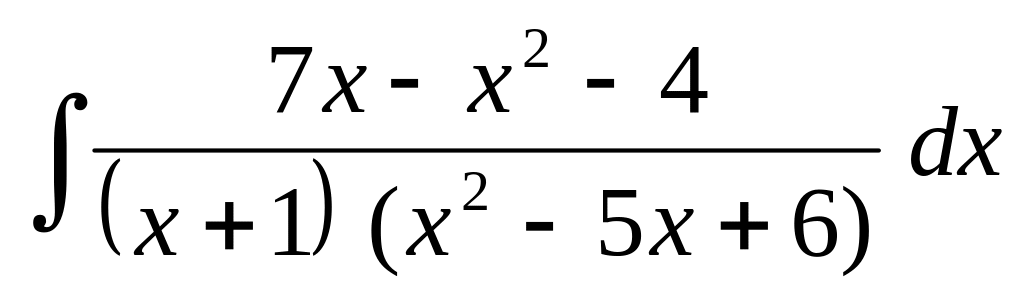5. Применяя тригонометрические подстановки, найти интеграл:

.

6. Вычислить интеграл от иррациональных функций:

.

7. Вычислить интегралы от тригонометрических функций:

   1. .

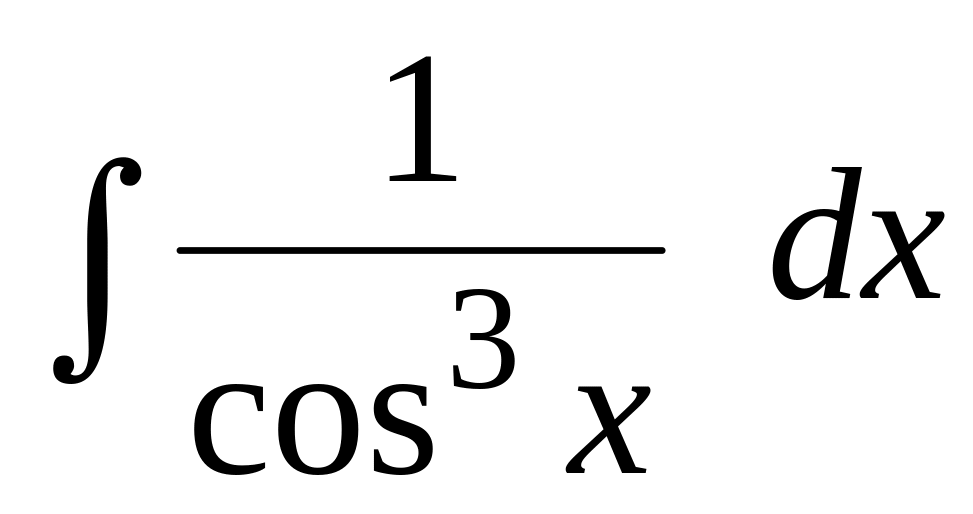   2. Используя тригонометрические подстановки, найти интеграл: .
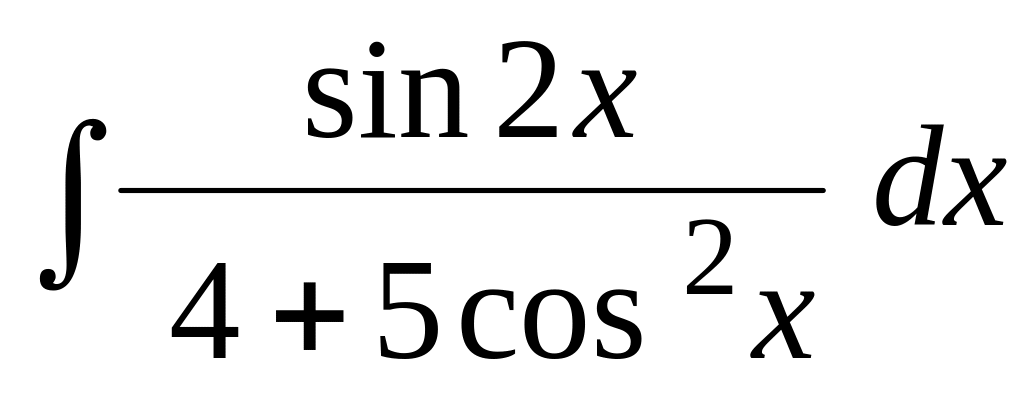