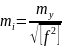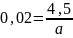Задачи:
1.Средняя квадратическая погрешность измерения угла равна 30″. Определить число измерений ,необходимое для получения результата со средней квадратической погрешностью не более 10″?
Дано: mn=30″,
m=10″
Найти: n-?
Решение: n=mn2/ m2=900/100=9 приёмов.
Ответ: n=9 приёмов.
2.
При проектировании
результатов измерений по первому
принципу (равенство погрешностей
измерений) требуется получить площадь
прямоугольника с погрешностью
при соотношении сторон
и погрешности измерения стороны
.
Найти длины сторон прямоугольника
и
,
удовлетворяющие поставленному условию
на погрешность площади.
Дано:
,
,
Найти:
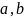
Решение. Составим функцию площади прямоугольника:
Учитывая то, что отношение сторон по длине , получим
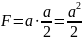
Найдем частную производную
Запишем формулу погрешности и подставим все имеющиеся данные
|
|
Выразим сторону и вычислим ее:
Зная соотношение, вычислим величину стороны :
Ответ:
,
.
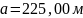3. В государственной сети 1 класса на концах базисных сторон определяют азимуты Лапласа А, которые вычисляют по формуле А=а-(λ-L)sinφ.Найти с какой точностью должны быть вычислены астрономический азимут а, разность долгот (λ- L) и широта φ,чтобы азимут был получен не грубее 0,5″ приданных φ=60˚, (λ- L)=15″?
Дано: φ=60˚,
(λ- L)=15″,
А=а-(λ-L)sinφ,
mA=0,5″
Найти: m-?
Решение:
А=а-(λ-L)sinφ,
Пусть m=mλ-L=ma=mφ
Ответ: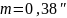
Вычисление весов измерений и функции.
Весом(Р) называют степень доверия к результату, который вычисляется как величина , обратно пропорциональная к точности получения результата, будь то измерение или функция от измерений.
,
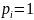μ=
i,
следовательно μ-погрешность единицы
веса.
Обратный
вес:
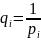
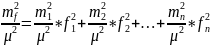
Задачи:
1.
Измерены 5 сторон теодолитного хода:
м,
м,
м,
м,
м.
Средняя квадратическая погрешность
линий определена по формуле
.
Найти веса всех сторон, приняв за единицу
вес линии длинной 100м?
Дано: м
м
м
м
м
Найти: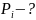
Решение:
,
,
,
,
,
,
,
,
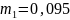Ответ: , , , ,
2.
Угол получен со средней квадратической
погрешностью
.
Сколько приемов нужно сделать инструментом,
дающим результат одного измерения со
средней квадратической погрешностью
,
чтобы веса углов оказались одинаковыми?
Дано:
,
,
Найти:
Решение.
Запишем формулу для нахождения средней
квадратической погрешности из
приемов:
Также нам известно, что веса этих измерений угла должны быть одинаковы:
|
|
|
|
Откуда выразим и вычислим количество приемов:
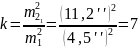
Ответ:
приемов.
3.Угол γ=α+β . Угол α получен как среднее из рез-ов измерений 20 приёмами со средней квадратической погрешностью ma=5″. Для угла β сделано 16 приёмов с mβ=8,4″. Определить вес угла γ, приняв за ед-цу веса результата измерений угла α одним приёмом.
Дано:γ=α+β
na=20 приёмов
ma1=5″
mβ1=8,4″
n β=16 приёмов
Найти:
Решение:
Ответ:
4.Стороны
м,
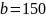м
прямоугольника измерены с весами
,
.Определить
вес вычисленной площади?
Дано: м
м
Найти: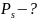
Решение:S=a*b,
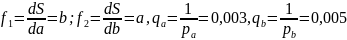
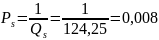
Ответ: