
- •1.Оценивание одной функции. Прямая задача.
- •Задачи:
- •1 . Найти ковариационную матрицу и коэффицент корреляции для определения координат в однократной линейной засечке при , , а базис безошибочен и имеет значение .
- •Предрасчёт точности результатов измерений. Задача проектирования.
- •Задачи:
- •Задача на совместный учёт систематического и случайного влияний.
Министерство Образования РБ
УО «Полоцкий Государственный Университет»
кафедра геодезии и кадастров
Лабораторная работа №3
Оценивание результатов косвенных измерений
Вариант 14
Выполнил: Лисенкова О.С.
Проверил: доц. Дегтярев А.М.
Новополоцк,2010
1.Оценивание одной функции. Прямая задача.
При
оценке точности косвенных измерений
по известной функции связи задача
ставится следующим образом: найти
среднюю квадратическую погрешность
 функции известного вида
функции известного вида
 ,
если даны погрешности её аргументов
,
если даны погрешности её аргументов
 .
С использованием правил нахождения
дисперсии от произвольной функции
находим окончательный вид оценки для
дисперсии D
исходной функции F.
В результате получаем следующую формулу
.
С использованием правил нахождения
дисперсии от произвольной функции
находим окончательный вид оценки для
дисперсии D
исходной функции F.
В результате получаем следующую формулу :
:

где (i=1,2,3,…,n; j=1,2,…,k).
С
учётом того, что ковариация связана с
погрешностями m
и коэффициентом корреляции r
как
 ,
а дисперсия равна
,
а дисперсия равна
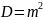 , для коррелированных измерений в
соответствии с (1), имеем:
, для коррелированных измерений в
соответствии с (1), имеем:

Если связи между i-тым и j-тым измерениями не существует (или она не значительна), то в формуле (2) отсутствует второе слагаемое.
Используя матричные обозначения, дисперсию функции можно представить в виде

Эта формула является выражением фундаментальной теоремы переноса ошибок. Здесь вектор-строка f из значений частных производных от функции F по i-тому аргументу:
 ,
,
а
 ковариационная
матрица результатов измерений, где
диагональные элементы – дисперсии i-го
измерения, недиагональные – ковариации.
ковариационная
матрица результатов измерений, где
диагональные элементы – дисперсии i-го
измерения, недиагональные – ковариации.
Задачи:
1.Среднее значение угла из четырёх приёмов имеет среднюю квадратическую погрешность 2˝. Определить погрешность угла, полученного при тех же условиях из 9 приёмов, и допустимую невязку в 9-угольнике.
Решение:
Погрешность
измерения угла n
приёмами:
 =
= ,где
,где
 - погрешность измерения угла одним
приёмом. Тогда
- погрешность измерения угла одним
приёмом. Тогда

Подставив
значения, при n=4
получим: =4˝
=4˝
Значит погрешность измерения угла 9 приёмами:
 =
= =1,33˝
=1,33˝
Допустимое значение невязки в k-угольнике из n приёмов определяется по формуле:

Подставив выраженное значение , получим при n=4:
 , где t-
вероятностный коэффициент.
, где t-
вероятностный коэффициент.
Вычислим: =2
=2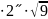 =12˝ , при t=2.
=12˝ , при t=2.
При
n=9
приёмах получим
:
= =8˝, при t=2.
=8˝, при t=2.
Ответ:
 =1,33˝;
при n=4
=12˝;
при n=9
=8˝.
=1,33˝;
при n=4
=12˝;
при n=9
=8˝.
2. Измерение угла одним приёмом даёт среднюю квадратическую ошибку, равную 15″. Какое минимальное число приёмов нужно сделать данным инструментом, чтобы получить среднюю квадратическую погрешность окончательного результата не более 5,0″?
Дано: mβ1=15″,
n1=1 приёмов,
mβ2=5″
Найти: n2-?
Решение:
 ,
отсюда m=
mβ1*
,
отсюда m=
mβ1* =15″
,
=15″
,
тогда n2=m2/ mβ22=9 приёмов.
Ответ: n2=9 приёмов.
3.Определить среднюю квадратическую погрешность вычисленного объёма прямоугольного параллелепипеда, если ребра его a=10м, b=4м, c=5м измерены со соедними квадратическими погрешностями ma= mb= mc=0,06м?
Дано: ma= mb= mc=0,06м,
a=10 м,
b=4 м,
c=5 м,
Найти: mv-?
Решение: V=a*b*c
fa=dV/da=b*c=20 м,
fb=dV/db=a*c=50 м,
fc=dV/dc=a*b=40 м,
mv2= ma2(fa2+ fb2+ fc2)=0.0036*(400+2500+1600)=16,16
mv=4,02 м
Ответ: mv=4,02 м.
4. Среднее значение угла из 6 приёмов имеет среднюю квадратическую погрешность 4,0″. Определить среднюю квадратическую погрешность вероятнейшего угла, полученного из 16 приёмов при тех же условиях?
Дано: n1=6 приёмов,
n2=16 приёмов,
mβ1=4″
Найти: mβ2-?
Решение: , отсюда m= mβ1* =9,8″
 9,8″/4=2,5″
9,8″/4=2,5″
Ответ: mβ2=2,5″
5. При каком угле наклона при измерении длины линии относительная погрешность поправки за наклон будет 1/2000 при измерении длины с относительной средней квадратической погрешностью 1/4000?
Дано:

Найти:φ-?
Решение: Δ=S-S*cosφ




По
принципу «равных влияний»


Ответ:
2.Оценивание точности вектор-функции.
В геодезической практике часто необходимо произвести оценку не одной функции, а нескольких, описывающих совместно какой-либо процесс. Для этого составляют вектор-функцию V, в виде столбца, состоящего из k функций, определяющих процесс:

считая,
что погрешности аргументов
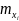 и теснота связи в виде ковариации или
коэффициента корреляции известны, на
следующем этапе составляется матрица
плана W,
состоящая из частных производных по
каждой строке в вектор-функции V
по всем аргументам-измерениям:
и теснота связи в виде ковариации или
коэффициента корреляции известны, на
следующем этапе составляется матрица
плана W,
состоящая из частных производных по
каждой строке в вектор-функции V
по всем аргументам-измерениям:

Полученная
матрица W
называется матрицей Якоби. Тогда, оценка
вектор-функции V
в виде ковариационной матрицы
 будет иметь вид
будет иметь вид
 ,
где
,
где
 - ковариационная матрица измерений.
- ковариационная матрица измерений.
Матрица может быть использована в промежуточных вычислениях для установления тесноты связи между элементами, которые в свою очередь связаны новой функциональной зависимостью.
