2. Математична індукція та геометрія.

Приклад 1. Довести, що кількість діагоналей d_n випуклого n – кутника можна обчислити за формулою .

Зазначимо, що n≥3, причому n може набувати лише натуральних значень. При n = 3 рівність справедлива

d_n = = = 0

Припустимо, що рівність справедлива для n = k

d_k =

Доведемо справедливість рівності для n = k + 1, тобто

d

A₃

_k+1 =

Щ

A₂

A₅

A₄

A_k

A ₁

об знайти кількість діагоналей (k+1) – кутника, потрібно додати до кількості діагоналей k – кутника кількість діагоналей, що виходять з (k + 1)-ї вершини A_{k + 1} та додати діагональ, що з’єднує

A₂

A₁

в

A_k+1

Малюнок 1

ершини A_k і A_1. З ескізу довільного многокутника (малюнок 1) очевидно, що з однієї вершини n – кутника виходить (n – 3) діагоналі.

Маємо: d_k+1 = d_k + (k + 1 – 3) + 1 = d_k + k – 2 + 1 = +1 = =

Отже, рівність доведено для усіх натуральних значень n.

3. Математична індукція і повсякденне життя.

Матіндукція, як не дивно, розповсюджена й в повсякденному житті.

Приклад. Є три стрижня та n кілець різного розміру (малюнок 2). На кільце можна класти тільки кільця, що менші за розмірами. Чи можливо перекласти вежуp з одного стрижня на інший?

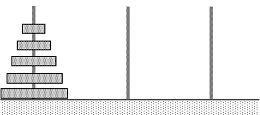
Малюнок 2

Вежу, в якій одне кільце (n=1) перемістити можливо.

Припустимо, що можливо перемістити вежу з n = k

Спробуємо навчитись перекладати пірамідку з n  = k  + 1 . Пірамідку з K кілець, що лежать на найбільшому k+ 1-м кільці, ми можемо згідно припущенню перемістити на будь-який стрижень. Зробимо це, перекладемо її на третій стрижень. Нерухоме  k + 1-е кільце не буде нам заважати провести алгоритм переміщення, так як воно найбільше. Після переміщення K кілець перемістимо k + 1-е кільце, яке залишилось, на другий стрижень. Ми можемо це зробити, так як другий стрижень вільний. Тепер звернемо увагу, той факт, що другий стрижень не пустий, не заважає перекладати на нього будь-які кільця, так як кільце на ньому найбільше (, будь-яке кільце можна покласти на більше за умовою задачі)і потім знов застосуємо відомий нам по припущенню алгоритм переміщення k кілець і перемістимо їх на другий стрижень, стрижень, на якому внизу лежить k + 1-е кільце. Таким чином, якщо ми вміємо переміщувати пірамідки з k кільцями, то вміємо переміщувати пірамідки і з k + 1кільцем.

4. Подвійна та потрійна математична індукція.

а) подвійна математична індукція

Подвійна матіндукція - це метод застосування математичної індукції, що заключає в собі використання методу матіндукції один раз, після чого доведення отриманого висновку за допомогою ще одного застосування методу математичної індукції з іншим індуктивним припущенням.

Приклад. Довести, що для будь – яких значень n справедливе твердження:

1. 3^{2n + 3} + 40n – 27 /./ 64

Для n = 1 рівність справедлива:

243 + 40 – 27 /./ 64

256 /./ 64

Припустимо, що для n = k твердження справедливе:

3^{2k + 3} + 40k – 27 /./ 64

Доведемо справедливість твердження для n = k + 1:

3^{2k + 5} + 40k + 60 /./ 64

3^{2k + 5} + 40k + 60 = 9*3^{2k + 3} + 40k – 27 + 40 =

= (3^{2k + 3} + 40k – 27) + (8*3^{2k + 3} + 40)

Перший доданок ділиться на 64 за припущенням. Доведемо, що й другий доданок ділиться на 64:

2. 8*3^{2k + 3} + 40 /./ 64

8(3^{2k + 3} + 5) /./ 64

3^{2k + 3} + 5 /./ 8

При k = 1 твердження справедливе:

243 + 5 /./ 8

248 /./ 8

Припустимо, що твердження справедливе для k = t:

3^{2t + 3} + 5 /./ 8

Доведемо справедливість твердження для k = t + 1:

3^{2t + 3} + 5 /./ 8

3^{2t + 5} + 5 = 9*3^{2t + 3} + 5 =( 3^{2t + 3} + 5) + 8*3^{2t + 3}

Перший доданок ділиться на 8 за припущенням, а другий складається з множників, один з яких – 8. Отже, 3^{2k + 3} + 5 ділиться націло на 8, а, отже, і перше твердження справедливе для усіх натуральних значень n.

б) потрійна математична індукція.

Потрійна матіндукція аналогічна подвійній, але якесь твердження, яке ми отримали в результаті подвійної математичної індукції ми маємо довести ще раз за допомогою матіндукції.

Приклад. Довести, що для будь – яких значень n справедливе твердження:

1. 2^{2n - 1} – 9n² + 21n – 14 /./ 27

Для n = 1 твердження правильне:

2 – 9 + 21 – 14 /./ 27

0 /./ 27

Припустимо, що для n = k твердження справедливе:

2^{2k - 1} – 9k² + 21k – 14 /./ 27

Доведемо справедливість твердження для n = k + 1:

2^{2k + 1} – 9(k + 1)² + 21(k + 1) – 14 /./ 27

2^{2k + 1} – 9(k + 1)² + 21(k + 1) – 14 = 4*2^{2k - 1} – 9k² – 18k – 9 +21k + 21 - - 14 = (2^{2k - 1} – 9k² + 21k – 14) + (3*2^{2k – 1} – 18k + 12)

Перший доданок ділиться націло на 27 за припущенням. Доведемо, що і другий доданок ділиться націло на 27:

2. 3*2^{2k – 1} – 18k + 12 /./ 27

3(2^{2k – 1} – 6k + 4) /./ 27

2^{2k – 1} – 6k + 4 /./ 9

При k = 1 твердження правильне:

2 – 6 + 4 /./ 9

0 /./ 9

Припустимо, що для k = t твердження справедливе:

2^{2t – 1} – 6t + 4 /./ 9

Доведемо справедливість твердження для k = t + 1:

2^{2t + 1} – 6t – 2 /./ 9

2^{2t + 1} – 6t – 2 = 4*2^{2t – 1} – 6t + 4 – 6 = (2^{2t – 1} – 6t + 4) + (3*2^{2t – 1} – 6)

Перший доданок ділиться націло на 9 за припущенням. Доведемо, що другий доданок теж ділиться націло на 9:

3. 3*2^{2t – 1} – 6 /./ 9

3(2^{2t – 1} – 6) /./ 9

2^{2t – 1} – 2 /./ 3

При t = 1 твердження справедливе:

2 – 2 /./ 3

0 /./ 3

Припустимо, твердження справедливе для t = m:

2^{2m – 1} – 2 /./ 3

Доведемо справедливість твердження для t = m + 1:

2^{2m + 1} – 2 /./ 3

2^{2m + 1} – 2 = 4*2^{2m – 1} – 2 = (2^{2m – 1} – 2) + (3*2^{2m – 1})

Перший доданок ділиться націло на 3 за припущенням, а другий складається з множників, один з яких – 3. Отже, твердження 2 і 3 справедливі для усіх натуральних значень t та m відповідно, з чого випливає справедливість твердження 1 для усіх натуральних значень n.