[Править] Влияние высоты над уровнем моря в тропосфере

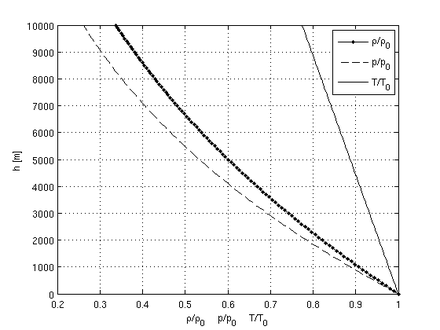
Зависимость давления, температуры и плотности воздуха от высоты по сравнению со стандартной атмосферой (p₀=101325 Па, T₀=288,15 K, ρ₀=1,225 кг/м³).

Для вычисления плотности воздуха на определенной высоте в тропосфере могут использоваться следующие параметры (в параметрах атмосферы указано зна­чение для стандартной атмосферы):

• стандартное атмосферное давление на уровне моря — p₀ = 101325 Па;

• стандартная температура на уровне моря — T₀ = 288,15 K;

• ускорение свободного падения над поверхностью Земли — g = 9,80665 ^м⁄_сек² (при данных вычислениях считается независимой от высоты величиной);

• скорость падения температуры (англ.)русск. с высотой, в пределах тропосферы — L = 0,0065 ^K⁄_м;

• универсальная газовая постоянная — R = 8,31447 ^Дж⁄_(Мол·K);

• молярная масса сухого воздуха — M = 0,0289644 ^кг⁄_Мол.

Для тропосферы (то есть области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте h над уровнем моря может быть задана формулой:

Давление на высоте h:

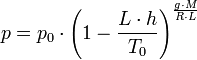
Тогда плотность может быть вычислена подстановкой соответствующих данной высоте h температуры T и давления P в формулу:

Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа. Графики нормализованы — показывают обший вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (термометра и барометра) на данный момент на уровне моря.

Уравнение состояния идеального газа

[править]

Материал из Википедии — свободной энциклопедии

Уравнение состояния

Статья является частью серии «Термодинамика».

Уравнение состояния идеального газа

Уравнение Ван-дер-Ваальса

Уравнение Дитеричи

Уравнение состояния Редлиха — Квонга

Уравнение состояния Барнера — Адлера

Уравнение состояния Суги — Лю

Уравнение состояния Бенедикта — Вебба — Рубина

Уравнение состояния Ли — Эрбара — Эдмистера

Разделы термодинамики

Начала термодинамики

Уравнение состояния

Термодинамические величины

Термодинамические потенциалы

Термодинамические циклы

Фазовые переходы

править

См. также «Физический портал»

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

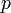•  — давление,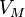

•  — молярный объём,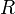

•  — универсальная газовая постоянная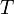

•  — абсолютная температура,К.

Так как , где  — количество вещества, а , где  — масса,  — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.)

С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода: