Теоретические сведения:

В математике много задач, связанных с вычислением производной функций и использованием геометрической интерпретации первой производной функции. Рассмотрим технологию построения касательной к заданной точке функции и определения параметров ее уравнения с помощью электронной таблицы MS Excel.

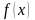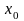Если задана функция , то первая производная функции в заданной точке с координатами и 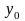является угловым коэффициентом касательной в этой точке. Уравнение касательной, проходящей через точку с координатами и , имеет вид:

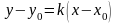, (1)

Где 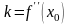- угловой коэффициент; и - координаты точки.

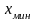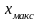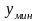Требуется построить график функции и касательную в прямоугольной области диаграммы, ограниченной минимальными и максимальными значениями абсцисс ( и ) и ординат ( и ).

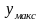Так как касательная является прямой линией, проходящей через заданную точку, то ее можно построить по координатам двух точек: 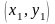и 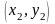, которые располагаются на границах прямоугольника (рис. 1).

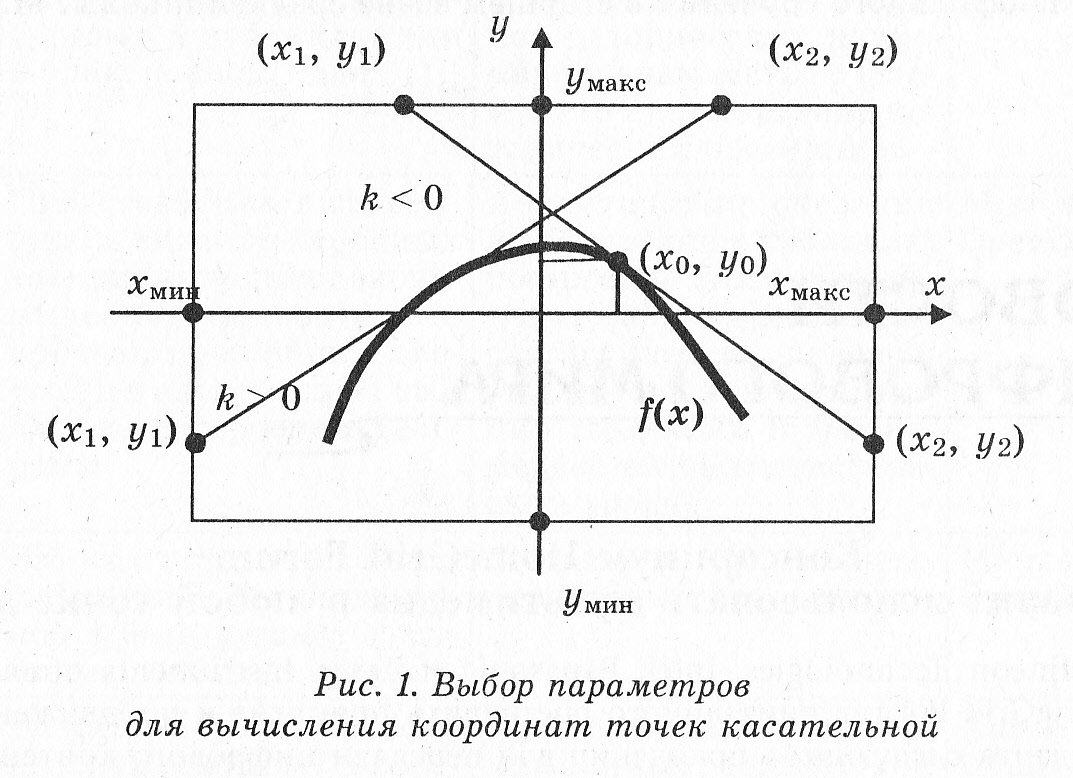
Найдем координаты точек касательной с учетом значения углового коэффициента . Значения углового коэффициента могут быть положительными, отрицательными, нулевыми или иметь бесконечно большие значения.

Пусть 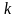> 0. Рассмотрим возможные варианты расположения точек. При 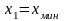с учетом формулы (1) .

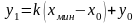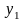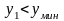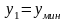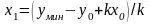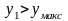Если выполняется неравенство < < , то координаты первой точки определены. В противном случае рассматриваем другие варианты расположения точки. При задаем и получаем . При задаем 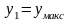и вычисляем .

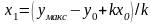Координаты второй точки касательной рассчитываются аналогичным образом. При этом задаем 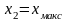и .

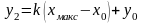Если выполняется неравенство <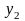 < , то координаты второй точки определены. В противно случае рассматриваем следующие варианты расположения точки. Пр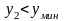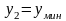и , и 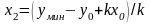. При выполнении неравенства 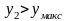задаем и подсчитываем .

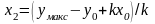Если 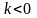, то получаем аналогичные выражения для определения координат точек касательной. При этом всегда в первую очередь рассчитываем правую точку касательной (рис. 1).

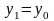При касательная является горизонтальной линией относительно оси аргументов. Следовательно, , и , .

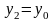Если 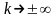, касательная становится вертикальной линией. Таким образом, 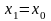, и , .

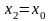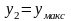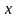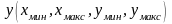Далее строим график функции и касательной в заданной точке посредством MS Excel. Определяем значения границ диапазонов для и при предварительном построении графика заданной функции.

Задание:

Формируем таблицы начальных условий задачи. Задаем ячейки: координат заданной точки функции ; углового коэффициента ; граничных значений диапазонов .

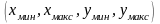Отступив одну ячейку от таблицы функции, рассчитываем координаты точек касательной с учетом приведенных выше рассуждений (рис. 2; в примечаниях отображены формулы расчетов). Предварительно для удобства вычисляем во вспомогательных ячейках значения при и при .

Выделим диапазон ячеек, который содержат ячейки таблицы функции и координат точек касательной. Обратимся к Мастеру диаграмм для построения графика функции и касательной. Задаем тип диаграммы – Точечная, а вид – Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров. Фиксируем минимальные и максимальные значения шкал осей и 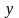в диалоговом окне Формат оси.

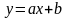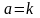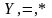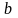Для наглядности одновременно вычислим параметры уравнения касательной , где из уравнения (1) , .Эти параметры рассчитываем в соответствующих ячейках, соседствующих с ячейками, в которых занесены символы для представления уравнения касательной. Так как значение параметра могут быть как отрицательными, так и положительными, то в соответствующей ячейке используем функцию ЕСЛИ для отображения символов «+» и «-».

На рис. 2 представлен пример построения касательной в заданной точке для синусоиды.

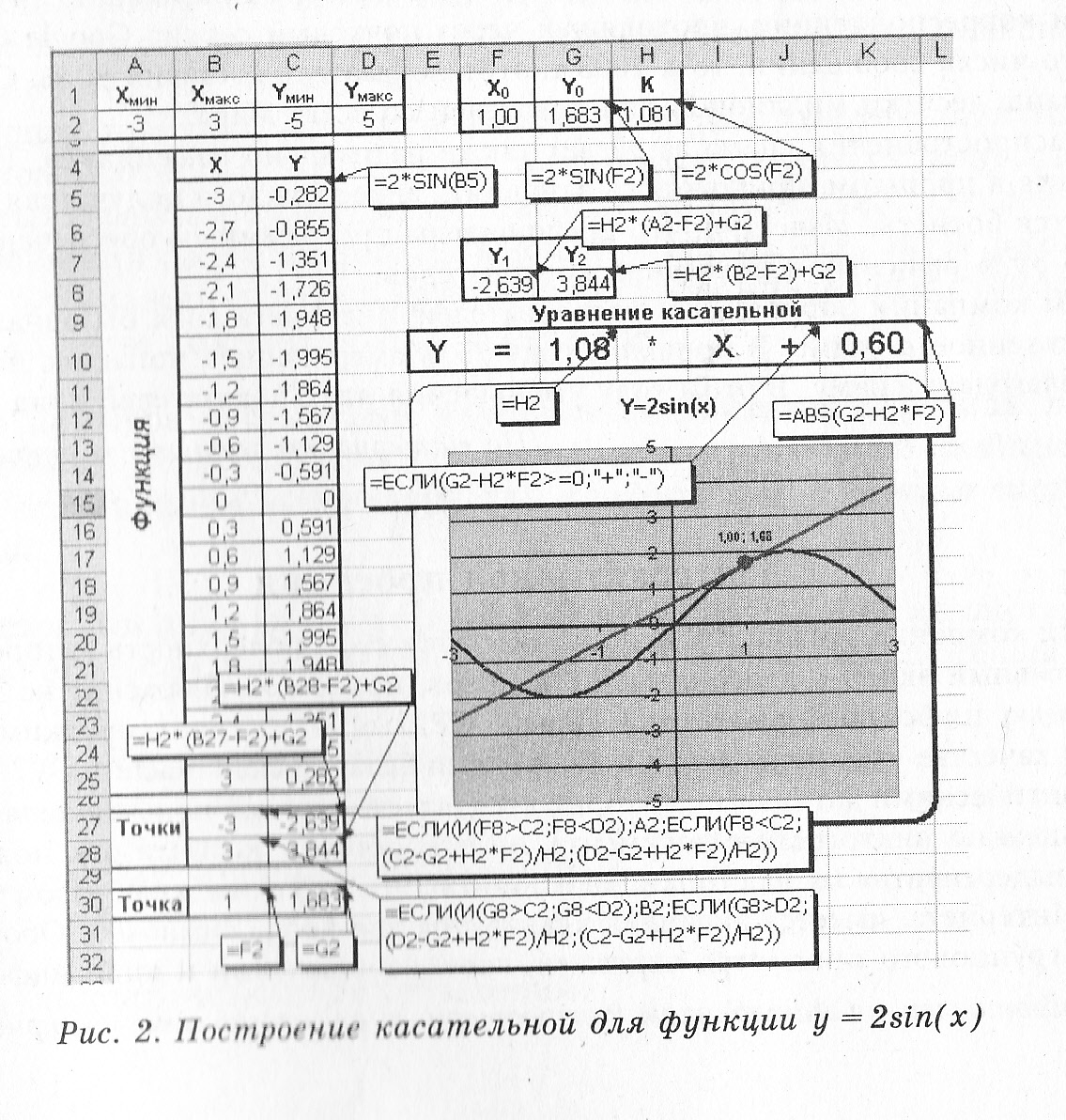
Целесообразно на графике добавить ячейки координат заданной точки для ее отображения. Для заданной точки, к которой строится касательная, можно установить отличительный маркер и вывести ее координаты. Для этого наведем курсор мыши на соответствующую точку диаграммы, вызовем контекстное меню, выделим пункт Формат точки данных. В появившемся диалоговом окне Формат элемента данных выберем нужный маркер, а так же параметры подписи данных. Чтобы установить цвет и толщину линии касательной, щелкнем по линии касательной. При появлении маркеров точек касательной вызовем контекстное меню и щелкнем по пункту Формат точки данных. В диалоговом окне установим тип, цвет и толщину линии касательной.

При необходимости можно дополнительно построить график производной заданной функции.