Задача 6.6

Имеются следующие данные о численности населения города за 5 лет (на начало года):

Год	2003	2004	2005	2006	2007
Численность населения, тыс. чел.	72	78	83	87	90

Найти линию тренда и, используя полученное уравнение, опре­делить численность населения в 2000 г. (прогноз).

Решение.

Предположив, что численность населения изменяется во вре­мени по прямой , для нахождения параметров а₀ и a_1, решаем систему нормальных уравнений, отвечающих требованию способа наименьших квадратов:

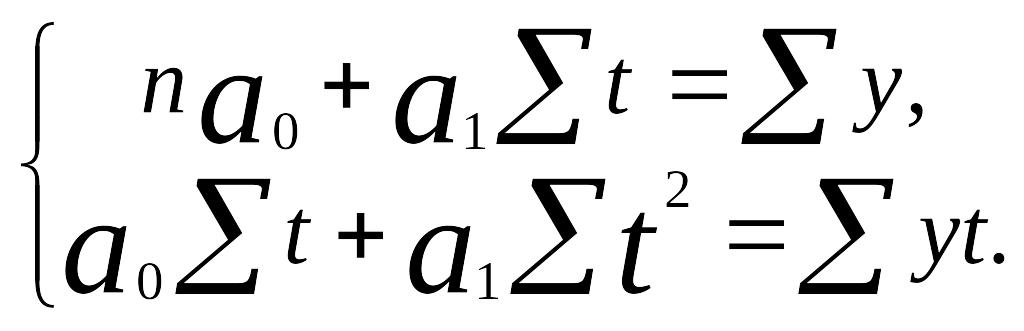
Далее в таблице рассчитаны необходимые для решения системы уравнений суммы: . Годы последовательно обо­значены как 1, 2, 3, 4, 5 (п = 5).

Подставляя полученные суммы в систему уравнений

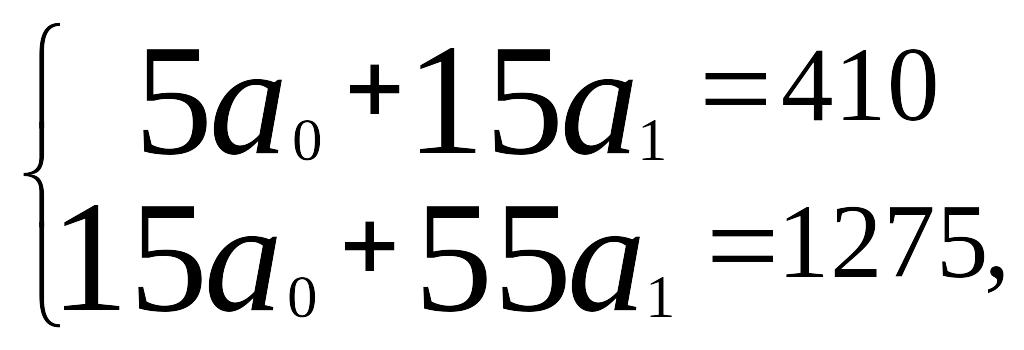
получаем a₁ = 4,5; a₀ = 68,5.

Отсюда искомое уравнение тренда = 68,5 + 4,5t. Подставляя в это уравнение значения t: 1,2, 3, 4, 5, находим выравненные (те­оретические) значения (см. графу 6 таблицы). Для 2000 г. t = 8.

Год	Числен­ность насе­ления, тыс. чел., уi	Условное обозначение времени t	t2	yt
1	2	3	4	5	6
2003 2004 2005 2006 2007	72 78 83 87 90	1 2 3 4 5	1 4 9 16 25	72 156 249 348 450	73 77,5 82 86,5 91
Σ	410	15	55	1275	410

Следовательно, по прогнозу численность населения города в 2000 г. составит 68,5 + 4,5 * 8 = 104,5 (тыс. чел.).

Для решения данной задачи можно использовать и второй спо­соб, упрощенный.

Как указывалось выше, если время (t) обозначить так, чтобы Σt=0 (т.е. счет вести от середины ряда), то система упростится и примет вид

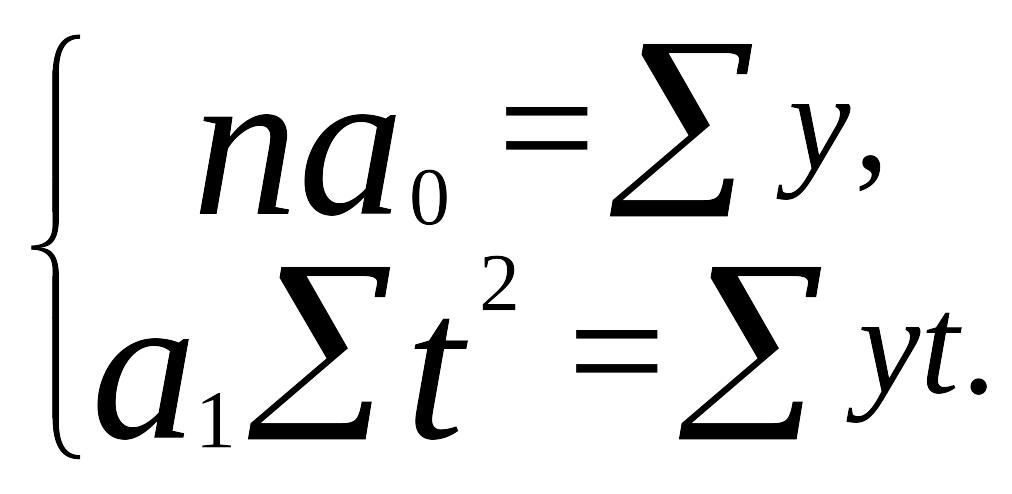
Каждое уравнение в этом случае решается самостоятельно:

и

Необходимые для расчета a_Q и a₁ суммы приведены ниже.

Условное обозначение времени, t	Год	Численность населения, тыс. чел., у	t2	yt
1	2	3	4	5	6
-2 -1 0 1 2	2003 2004 2005 2006 2007	72 78 83 87 90	4 1 0 1 4	-144 -78 0 87 180	73,0 77,5 82,0 86,5 91,0
Σt=0	п = 5	Σy = 410	Σt2= 10	Σyt = 45	=410

Получаем

5a₀₌410; a₀=82;

10a₁=45; a₁=4,5;

отсюда уравнение прямой для выровненных уровней

=82+4,5t(линия тренда).

Выровненные значения, рассчитанные по последней формуле путем подстановки в нее значений t = —2, — 1, 0, 1, 2, показаны в графе 6 таблицы.

Численность населения в 2000 г. (t = 5) по формуле будет

= 82 + 4,5*5 = 104,5 (тыс. чел.).

Естественно, эта величина условная, рассчитанная при предпо­ложении, что линейная закономерность изменения численности на­селения, принятая для 2003—2007 гг., сохранится на последующий период до 2000 г.