Практическая работа 1 системы счисления

Цель работы:

1 Дать понятие о различных системах счисления применяемых в информатике.

2 Привить навыки по переводу числа из одной системы счисления в другую.

3 Научить производить математические операции над целыми и вещественными числами в различных системах счисления.

Краткие теоретические сведения Системы счисления

До изучения информатики Вам приходилось сталкиваться с различными системами счисления: троичная, десятеричная, двенадцатеричная.

Для представления информации в ПЭВМ применяются следующие системы счисления (с/с): двоичная, восьмеричная, шестнадцатеричная, двоично-десятеричная. В таблице 1.1 приведены числа в различных системах счисления. Незначащие нули (это нули, стоящие в целой части числа левее старшей значащей цифры, а в дробной части числа – правее последней значащей цифры) – это скорее дань традиции. Они предназначены для того, чтобы количества бит в числе было кратно четырём, поэтому при операциях с числами в различных с/с они отбрасываются. Хотя результат, записанный в классическом виде, выглядит лучше. Для упрощения подачи материала числа в двоичной с/с компонованы следующим образом:

0 111 – при данной записи: “111” – это триада цифр, а “0111” – это тетрада цифр. Символом апостроф “ ’ ” отделяются друг от друга тетрады.

Система счисления указывается в нижнем индексе, который ставится после самого числа, например:

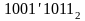
Таблица представления чисел в различных с/с Таблица 1.1

2	8	10	2-10	16	2	8	10	2-10	16
0 000	0	0	0000	0	001 001	11	9	1001	9
0 001	1	1	0001	1	001 010	12	10	0001’0000	A
0 010	2	2	0010	2	001 011	13	11	0001’0001	B
0 011	3	3	0011	3	001 100	14	12	0001’0010	C
0 100	4	4	0100	4	001 101	15	13	0001’0011	D
0 101	5	5	0101	5	001 110	16	14	0001’0100	E
0 110	6	6	0110	6	001 111	17	15	0001’0101	F
0 111	7	7	0111	7	0001’0000	20	16	0001’0110	10
001 000	10	8	1000	8	0001’0000	21	17	0001’0111	11