Санкт-Петербургский государственный электротехнический университет

“ЛЭТИ”

кафедра физики

ОТЧЕТ

по лабораторно-практической работе № 10 (4)

ИССЛЕДОВАНИЕ ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ

Выполнил Гирфанов А.С.

Факультет ЭА

Группа № 6412

Преподаватель Попов Ю.И.

Оценка лабораторно-практического занятия
Выполнение ИДЗ	Подготовка к лабораторной работе	Отчет по лабораторной работе	Коллоквиум		Комплексная оценка

“Выполнено” “” ноября 2006

Подпись преподавателя __________

ЛАБОРАТОРНАЯ РАБОТА № 10

ИССЛЕДОВАНИЕ ТЕРМОДИНАМИЧЕСКИХ ЦИКЛОВ

ЦЕЛЬ РАБОТЫ: исследование политропно-изохорно-изотермического (nVT) и адиабатно-изохорно-изотермического (SVT) циклов.

СХЕМА УСТАНОВКИ И МЕТОД ИЗМЕРЕНИЙ

Приборы и принадлежности: баллон с воздухом, манометр, микрокомпрессор, лабораторные термометр и барометр.

И спользуемая в работе установка изображена на рис. 2.1. Баллон А объёмом V₁ может сообщаться либо с насосом H, либо с атмосферой. Внутрь баллона помещён манометр М, измеряющий избыточное давление. Одно деление шкалы равно 4 мм вод. ст., что составляет 40 Па. Рабочим газом является воздух.

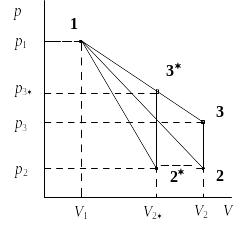
В исходном состоянии параметры состояния воздуха следующие: давление p₂ и температура T₁. Диаграмма исследуемого цикла в координатах давления p и объёма V показана на рис. 2.2.

Исходным является состояние, в котором воздух имеет давление p₂ и температуру T₁. Насосом в баллон накачивают воздух до давления p₁ = p₂ + p₁ (состояние 1 (p₁; V₁)). При сжатии воздух нагревается, поэтому после закрытия крана необходимо выждать некоторое время, пока температура воздуха в баллоне не сравняется с температурой окружающей среды (при этом прекращается движение стрелки манометра).

Затем воздух выпускают через кран К в атмосферу в течение нескольких секунд. Когда стрелка манометра приблизится к нулю, кран закрывают. В этот момент давление воздуха баллоне становится p₂ (состояние 2 (p₂; V₂). Изменение параметров состояния воздуха в процессе расширения отражает линия 12, которая является политропой.

После закрытия крана охлаждённый при расширении воздух изохорически нагревается до температуры окружающей среды в результате теплообмена. Изменение параметров состояния воздуха отражает линия 23, которая является изохорой. Температура воздуха в баллоне становится равной температуре в точке 1 (T₃ = T₁), следовательно, точки 1 и 3 лежат на одной изотерме.

После выравнивания температур давление в баллоне изменится на p₃ и станет p₃ = p₂ + p₃ (состояние 3 (p₃; V₂)). Таким образом, p₁ и p₃  это изменения давления на участках 12 и 23. Участки 12 и 13 на диаграмме можно аппроксимировать прямыми, так как изменения параметров p, V, T в данной работе малы и много меньше абсолютных значений соответствующих величин.

В работе изучаются политропно-изохорно-изотермический (nVT) и адиабатно-изохорно-изотермический (SVT) циклы путем их моделирования при значениях показателя адиабаты γ = 1,4 и показателя политропы n, полученным в результате измерений.

Основные расчетные формулы

1. Показатель политропы n при известных изменениях давлений Δp₁, Δp₃.

Продифференцируем уравнения политропы (рVⁿ = const) и изотермы (рV = const):

рnV ^n1 dV + V ⁿ dр = 0  для политропы

рdV + V dр = 0  для изотермы

Преобразуем соотношения к виду

При относительно малых изменениях p и V угловые коэффициенты политропы и изотермы рассчитываются по формулам

, где V = V₂  V₁.

Из отношения приведенных уравнений получаем

2. Холодильные коэффициенты ε для nVT и SVT- процессов при известных давлениях p₂ и изменениях давлений Δp₃, Δp₃^*.

Холодильный коэффициент  определяется как отношение теплоты, отнятой от охлаждаемого газа, к затраченной в цикле работе. Для SVT-цикла

Для nVT-цикла

Перепишем выражения для , используя экспериментально измеренные величины давлений, для чего значения работы А₁₂ и А_12* определим графическим способом. В рV-координатах (рис. 2.2) они равны площадям трапеций, основания которых р₁ и p₂ = р₂^*, а высоты  (V₂ V₁) и (V₂^*  V₁) соответственно. После преобразований получаем:

3. Холодильный коэффициент обратного цикла Карно ε_K при известных температурах нагревателя и холодильника T₁, T₂.

КПД прямого цикла Карно по определению равен .

Холодильный коэффициент обратного цикла Карно .

4. Число молей воздуха в сосуде по известным значениям p₂, V₁, T₁:

Запишем уравнение состояния идеального газа для процесса 1-2:

5. Изменения энтропии ΔS при известных давлениях Δp₁ и p₂, показателе политропы n и количестве молей газа ν.

По определению .

nVT: На участке 12 (политропический процесс)

S₁₂ =

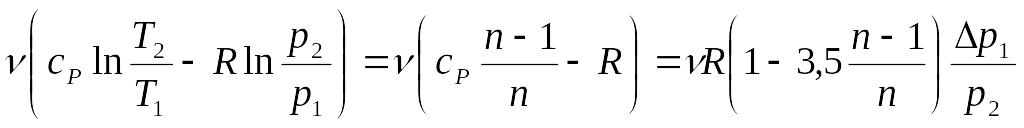
На участке 2-3 (изохорический процесс)

S₂₃ =

На участке 3-1 (изотермический процесс)

S₃₁ =

SVT: На участке 12^* (адиабатический процесс) изменение энтропии равно нулю.

Изменения энтропии на участках 2-3 (изохорический процесс) и 3-1 (изотермический) равны по величине, но различаются знаком:

S_3*1 =

Протокол наблюдений

Лабораторная работа № 10 : исследование термодинамических циклов

Таблица измерений

Атмосферное давление p₂ = 102100 Па

Температура воздуха T₁ = 294 К

N	1	2	3	4	5	6	7	8	9	10
Δp1, Па	670	680	680	680	690	690	700	700	710	720
Δp3, Па	100	110	130	150	120	110	140	150	120	110

Экспериментальный макет

Объем баллона V₁ = 22,4 л = 22,4∙10^-3 м³

Выполнил Гирфанов А.С.

Факультет ЭА

Группа № 6412

“ ” ноября 2006

Преподаватель: Попов Ю.И.

Протокол наблюдений подписывается преподавателем в конце лабораторного занятия.

ОБРАБОТКА РЕЗУЛЬТАТОВ

1. а) Определение избыточных давлений Δp₁ и Δp₃ (прямые измерения):

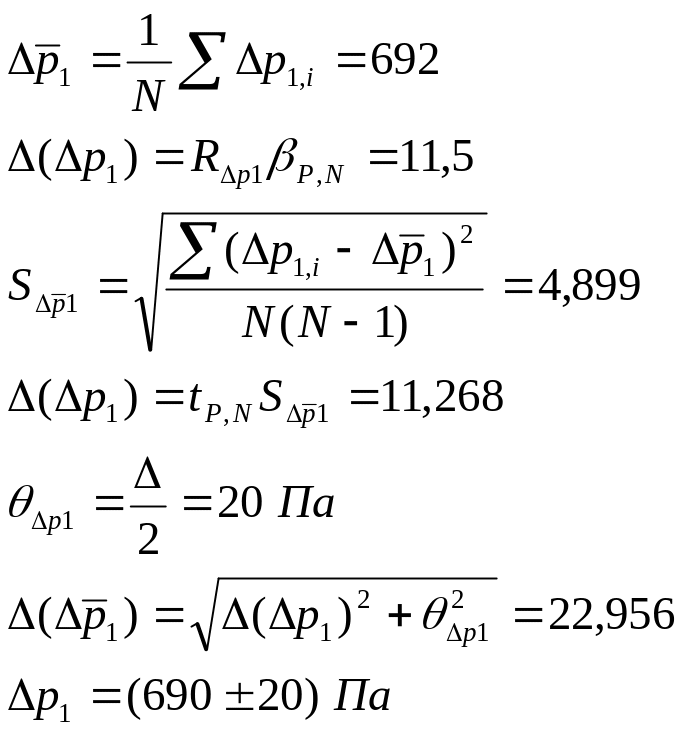
б) Определение показателя политропы n (перенос погрешностей.)

2. Определение параметров состояния (p, V, T) в точках 1, 2, 3, 1^*, 2^*, 3^*.

Cостояние 1 (совпадает с 1^*):

p₁ = p₂ + Δp₁ = 102790 Па

V₁ = 22,4 л = 22,4∙10^-3 м³

T₁ = 294 K

Состояние 2^*:

p₂^* = p₂ = 102100 Па

Уравнение адиабаты:

Газ двухатомный, i = 5.

Уравнение состояния:

Cостояние 3^*:

T₃^* = T₁ = 294 K

Из уравнения изотермического процесса 1-3:

Процесс 2-3 изохорический, значит V₃^* = V₂^*.

Тогда имеем

Уравнение состояния:

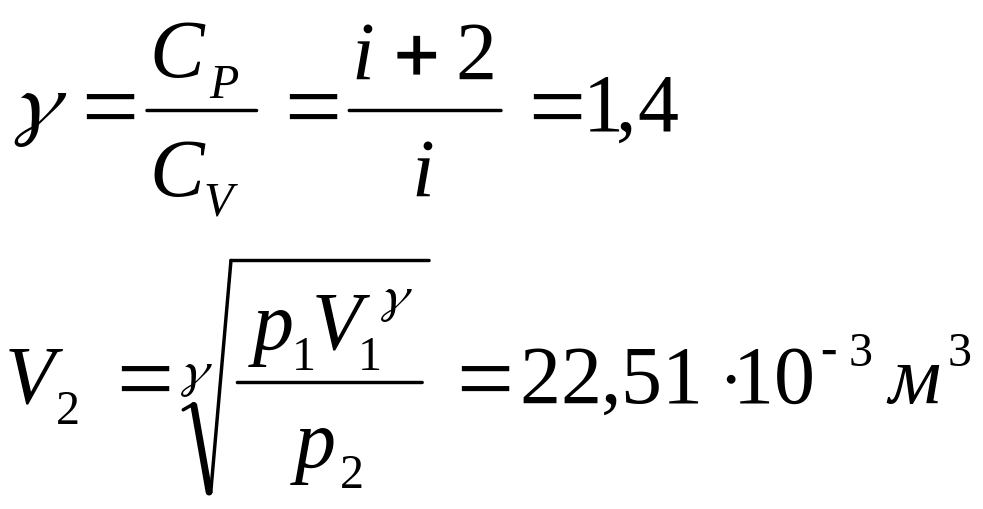
Состояние 2:

p₂ = 102100 Па

Уравнение политропы:

Уравнение состояния:

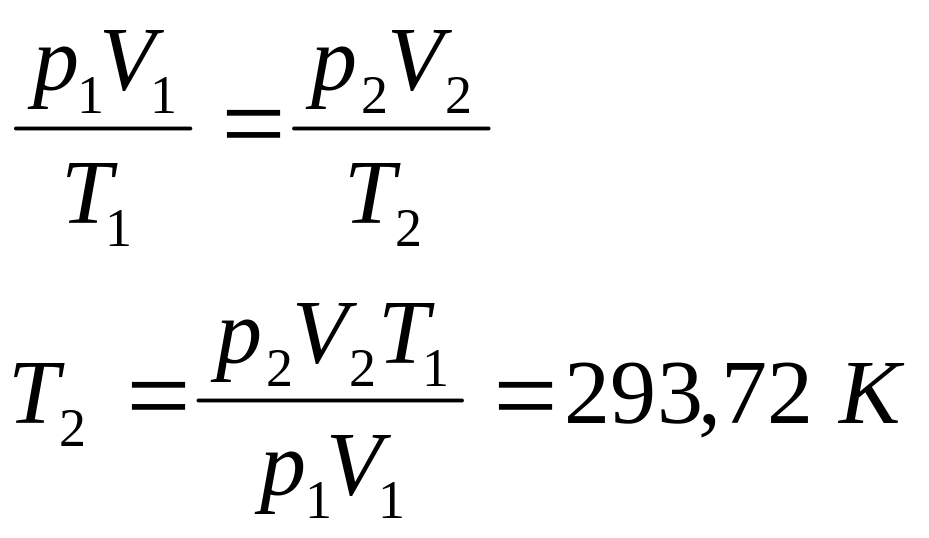
Cостояние 3:

p₃ = p₂ + Δp₃ = 102220 Па

T₃ = T₁ = 294 K

Уравнение состояния:

Графики циклов (начало координат сдвинуто):

nVT (n = 1,2)

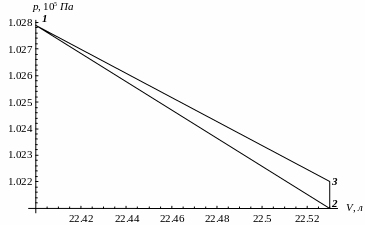
SVT (γ = 1,4)

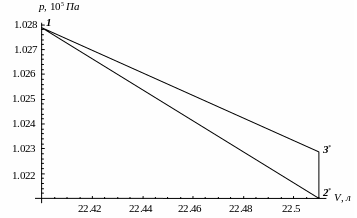
3. Расчет холодильных коэффициентов ε (вывод формул – стр. 3).

Цикл nVT (1-2-3-1):

Цикл SVT (1-2^*-3^*-1):

Так как Δp₃^* > Δp₃, .

Обратный цикл Карно (идеальная холодильная машина):

Для T₁, T₂:

Для T₁, T₂^*:

Так как T₂^* < T₂, .

Холодильные коэффициенты циклов Карно меньше, чем холодильные коэффициенты рассматриваемых циклов в силу идеальности холодильной машины Карно.

4. Определение числа молей воздуха ν в сосуде (вывод формул – стр. 3).

5. Изменение энтропии ΔS в циклах 1-2-3-1, 1-2^*-3^*-1 (вывод формул – стр. 4).

Цикл nVT (1-2-3-1):

Политропа 1-2

Изохора 2-3

Изотерма 3-1

Изменение энтропии за цикл

Цикл SVT (1-2^*-3^*-1):

Адиабата 1-2^* ΔS₁₂ = 0

Изохора 2^*-3^*

Изотерма 2^*-3^*

Изменение энтропии за цикл

ИТОГИ

Таблица измерений
N	1	2	3	4	5	6	7	8	9	10
Δp1, Па	670	680	680	680	690	690	700	700	710	720
Δp3, Па	100	110	130	150	120	110	140	150	120	110

Вычисленные величины

Избыточное давление Δp1 = (69020) Па

Избыточное давление Δp3 = (12020) Па

Избыточное давление Δp3* = 188 Па

Показатель политропы n = = (1,20,4)

Параметры состояния p, V, T
Состояние	p, Па	V, м3	T, К
1	102790	22,4∙10-3	294
2	102100	22,53∙10-3	293,72
3	102220	22,53∙10-3	294
2*	102100	22,51∙10-3	293,46
3*	102288	22,51∙10-3	294

Изменение энтропии ΔS
Процесс	ΔS, Дж/К
1-2	21,9∙10-3
2-3	21,9∙10-3
3-1	–43,8∙10-3
1-2*	0
2*-3*	37,5∙10-3
3*-1	–37,5∙10-3

ВЫВОДЫ

Выполнив данную лабораторную работу, я исследовал политропно-изохорно-изотермический (nVT) и адиабатно-изохорно-изотермический (SVT) циклы.

Пользуясь экспериментально измеренными величинами избыточных давлений Δp₁ и Δp₃, я определил показатель политропного процесса n, нашел холодильные коэффициенты ε для nVT- и SVT-циклов.

С помощью уравнения состояния идеального газа мной были вычислены параметры состояния (p, V, T). На основе полученных данных я построил графики nVT- и SVT-циклов в pV-координатах.

Также были найдены изменения энтропии ΔS для каждого процесса nVT- и SVT-циклов.

Результаты работы помещены на лист «Итоги» в табличной форме.