Reshenia_pervogo_varianta

1. Случайная величина ξ принимает значение номера Вашего варианта с вероятностью 1. Составьте закон распределения этой случайной величины, найдите значения , где N – номер варианта, и изобразите график функции распределения.

Решение. Эта задача исключительно на определения. НИЧЕГО сложного в ней нет. Прежде всего, вспомним, что называется законом распределения СВДТ. Это функция, заданная таблицей. В первой строке пишут те значения, которые СВ принимает, во второй – соответствующие вероятности. Так что в нашем случае это будет таблица из одного столбца.

	1
	1

Найдем значения функции распределения. Заметим, что .

, ,

Построим график функции распределения. Не забудьте ПРАВИЛЬНО подписать оси.

2. Игрок в казино 2 раза ставил на чёт, первая ставка была 1 у.е., вторая – 2 у.е. При выпадении чётного числа игрок получает удвоенную ставку, в противном случае ставка уходит в доход казино. Составьте закон распределения случайной величины  – выигрыш игрока. Найдите .

Решение. Будем считать, что выпадение чётного или нечетного числа равновероятны, то есть если событие Ч – выпало чётное число очков, а Н – выпало нечётное число, то . Найдем все возможные значения случайной величины (учтите, что проигрыш – это отрицательный выигрыш), а случайная величина – числовая функция, заданная на элементарных исходах эксперимента. Таким образом, если игрок 2 раза делал ставку, то пространство элементарных исходов эксперимента .

/здесь с минусом стоят его ставки, а с плюсом – получаемый выигрыш/

То есть случайная величина принимает 4 возможных значения. Легко заметить, что , так как, например, . Составим закон распределения (см. выше, что это такое).

	– 3	– 1	1	3
	1/4	1/4	1/4	1/4

Осталось найти числовые характеристики - математическое ожидание, дисперсию и среднее квадратическое отклонение.

,

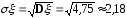
3. Выведите формулу для вычисления математического ожидания случайной величины ξ, распределенной по биномиальному закону с параметрами , .

Решение. Это мы делали на лекции в общем случае. Если хотите получить максимально возможное число баллов за этот номер, то нужно сразу рассматривать частный случай, а не писать «по памяти» общий вывод, после чего подставлять нужные числа. Нужен именно вывод, а не ответ, пусть даже правильный.

4. Дана плотность распределения случайной величины . Найдите параметр γ, .

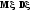Решение. Это мы тоже делали на лекции. Главная суть задания заключается в том, что надо помнить формулу для плотности нормального распределения. Брать неберущиеся интегралы в этом задании не предполагается. Так вот, вспомним, что нормальное распределение (распределение Гаусса) имеет плотность , причем параметры распределения 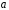и 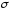суть математическое ожидание и среднее квадратическое отклонение случайной величины. Так что задача сводится к рассмотрению дроби в показателе степени и выделению полного квадрата. Ответы будут получаться в обратном порядке, то есть сначала дисперсия, потом мат. ожидание и уже следом за ними – параметр γ.

, из чего заключаем, что , , 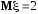а поскольку 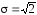, получаем .

5. Дана плотность распределения случайной величины ξ : Найдите параметр .

Решение. В этом задании у Вас будет 2 варианта решения – или честно вычислять интегралы и подбирать сначала допустимое значение для параметра, затем вычислять числовые характеристики, или использовать известные распределения (равномерное или показательное – как повезет). Нужные интегралы я запишу, конечно, но брать не буду, потому что хочу пойти вторым путем, то есть схитрить.

Для вычисления λ можно воспользоваться условием нормировки плотности, то есть .

В нашем случае, учитывая специфику плотности, . Из этого условия Вы найдете λ, если не поленитесь.

Осталось взять еще 2 интеграла: , . Оба интеграла берутся по частям.

Решим эту задачу по-другому, используя те факты, которые были получены на лекции для показательного распределения, потому что данное распределение лишь чуть-чуть от него отличается. Легко заметить, что в этом случае. .

6. Случайная величина 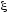распределена по закону . Найти .

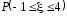Решение. Здесь речь идет о нормальном распределении с параметрами , плотность распределения которого 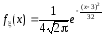. Используем формулу: .

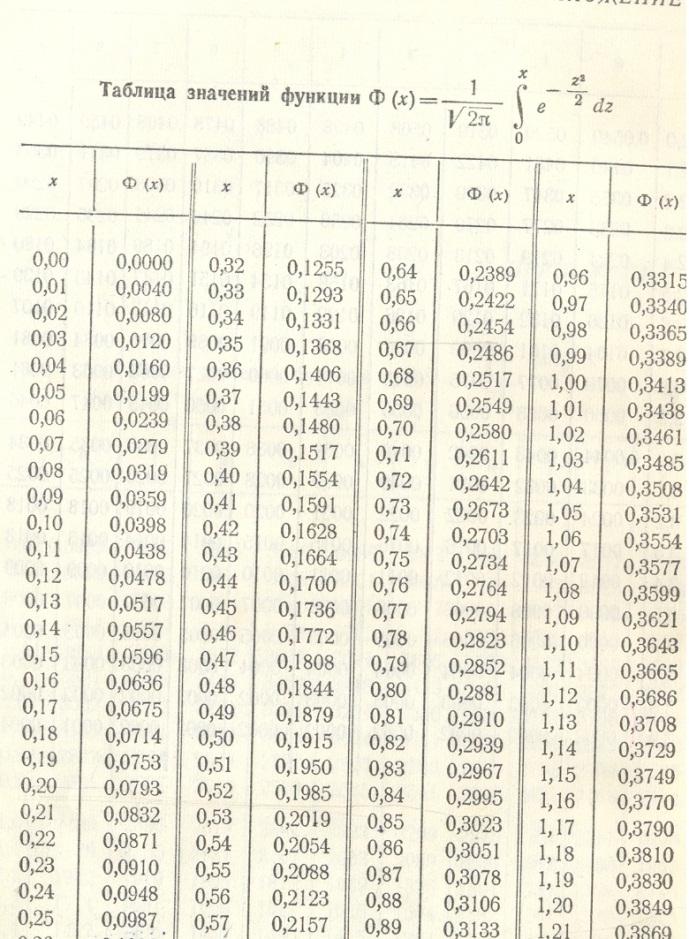
Таблицу постарайтесь найти и принести с собой. Если что, то несколько штук я возьму, конечно :)).

7. Поезд движется равномерно со скоростью 80 км/час. Случайная величина ξ – показания спидометра в некоторый произвольный момент времени. Эта случайная величина может иметь:

А) распределение Пуассона;

В) биномиальное распределение;

С) геометрическое распределение;

D) равномерное распределение;

Е) показательное распределение;

F) нормальное распределение.

Что можно сказать о параметрах и числовых характеристиках этого распределения?

Решение. Учитывая тот факт, что приборы (в данном случае спидометр) всегда показывают с некоторой степенью точности, а также то, что при стуке колес, возможно, стрелка не является неподвижной, речь идет о нормальном распределении (F). По данным задачи мы можем определить только параметр . Он же равен математическому ожиданию.

8. На рисунке изображены плотности распределений двух случайных величин ξ и η, подчиняющихся нормальному закону с целыми параметрами. Справедливо утверждение:

1. ;

2. ;

3. ;

4. ;

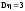5. нет правильного ответа.

Решение. Сначала по графикам плотностей распределений найдем те самые целые параметры распределений. Для случайной величины ξ (красная линия) . Чтобы определить второй параметр σ можно или воспользоваться тем, что плотность имеет максимум при и равен он , но это не очень удобно. Лучше вспомнить правило «трех сигм», по которому с вероятностью 0,997 случайная величина принимает значение в промежутке 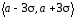. По графику видно, что для случайной величины ξ этот промежуток , а поскольку , то . Так что случайная величина ξ имеет распределение . Аналогично, случайная величина η распределена по закону . Значит, , . То есть утверждения А) и С) справедливы, а D) – нет. Проверим утверждение В). По свойству мат. ожидания . Правильный ответ: А), С).

9. Распределение двумерного случайного вектора задано таблицей. Найдите коэффициент корреляции случайных величин 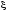и 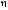. Сделайте вывод о степени зависимости этих случайных величин.

Решение. Составим законы распределений случайных величин ξ и η, а также найдем их числовые характеристики.

ξ	– 1	0	1
	1/6	1/3	1/2

η	0	1
	1/3	1/6+1/2=2/3

,

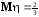Чтобы вычислить коэффициент корреляции, нужно еще составить закон распределения произведения случайных величин. По исходной таблице видим, что возможные значения для произведения – это 0, – 1 и 1.

ξη	– 1	0	1
	1/6	1/3	1/2

Осталось вычислить коэффициент корреляции и сделать вывод о степени зависимости случайных величин.

.

Поскольку коэффициент корреляции отличен от нуля, случайные величины наверняка являются зависимыми, но т.к. коэффициент отличается от единицы (по модулю), эта зависимость не сильно напоминает линейную. /Заметим, что если коэффициент корреляции равен нулю, то это еще не значит, что случайные величины независимые/.

10. Дан статистический ряд: .

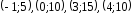• Найдите объем выборки

• Постройте полигон частот

• Найдите моду

• Найдите медиану

• Найдите межквартильный размах

• Постройте график эмпирической функции распределения

• Вычислите выборочное среднее

• Найдите выборочную дисперсию

• Найдите исправленную выборочную дисперсию

Решение. Статистический ряд – это множество пар чисел, в которых первое число равно значению выборки, а второе – его частота. То есть, например, число 0 в выборке встречается 10 раз.

• Объем выборки – число значений в ней (число измерений соответствующей случайной величины). В нашем случае .

• Полигон частот – многоугольник, вершинами которого являются точки, координаты которых заданы статистическим рядом. Постройте, пожалуйста, сами…

• Мода – то значение, которое встречается чаще всего. Здесь .

• Так как у нас 40 значений случайной величины, то медиана – среднее арифметическое 20-го и 21-го значений вариационного ряда (последовательности из всех 40 значений случайной величины, записанных в порядке возрастания). .

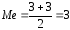• Межквартильный размах – разность между третьей и первой квартилью. .

• График эмпирической функции распределения совпадает с графиком функции распределения СВДТ, закон которой задан таблицей (см. ниже). Постройте его, пожалуйста, сами.

  – 1	0	3	4
  5/40	10/40	15/40	10/40

• Выборочное среднее

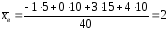
• Выборочная дисперсия (являющаяся смещенной состоятельной оценкой дисперсии)

• Исправленная выборочная дисперсия хороша тем, что кроме состоятельности является также несмещенной оценкой дисперсии. Вычисляется она очень просто: 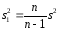, а при больших объемах выборки мало отличается от обычной выборочной дисперсии.

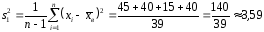
На этом все – остальное скажу на консультации. Удачи!