ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

«Математику уже затем учить надо, что она ум в порядок приводит».

М.В. Ломоносов

Логика (от древнегреческого logos – слово, выражающее мысль) является началом любой научной теории. Логика как наука о способах мышления, приводящих к истине, возникла в глубокой древности.

Начало науки о законах и формах мышления связывают с именем Аристотеля. Именно Аристотелем (384–322 гг. до н.э.) создана чистая система силлогизмов – правил вывода, что и привело к возникновению теории логики. Математическое исследование этих вопросов берет свое начало от основополагающего труда Джорджа Буля, изданного в Лондоне в 1854 году. Этот труд Буля положил начало математической логики, систематическое развитие которой было достигнуто работами многих математиков XX века.

Правила вывода позволяют преобразовывать исходные утверждения подобно тому, как тождественные преобразования в математике дают возможность решать различные системы уравнений. Следующим шагом формализации логики является появление специальной символики для точной и компактной записи утверждений и определения операций над ними.

Идея перенесения тех методов, которые обычно применяются в математике, на логику была реализована Б. Паскалем (1646-1716), Г. Лейбницем (1646-1716), Дж. Булем (1815-1864), О. Де Морганом (1806-1871), Г. Фреге (1848-1925), Б. Расселом (1872-1970), Д. Гильбертом (1862-1943), А. Марковым (1903-1979) и др. Так появился язык логики как логическое продолжение языка математики.

С появлением языка математической логики стало возможным составлять алгоритмы логического вывода. Стали вести речь о создании «искусственного интеллекта». В последнее время логика находит все более широкое применение в технике при исследовании и разработке вычислительных машин, дискретных автоматов. Ее методы используются в теории преобразования и передачи информации, теории вероятностей и комбинаторном анализе. Математическая логика находит свое применение в экономике, биологии, медицине, психологии, праве, языкознании.

Сложившийся стереотип о том, что математическая логика – наука, изучающая законы мышления с применением аппарата математики, главным образом, для нужд самой математики, в современных условиях меняется коренным образом. С расширением области применения и дальнейшим развитием математической логики изменяется и взгляд на нее. Объектами математической логики являются любые дискретные конечные системы, а ее главная задача – структурное моделирование таких систем.

В элементарной алгебре буквами обозначаются в основном числа. В логике же буквами обозначаются логические объекты, например, предложения. Под предложением понимается тоже, что и в грамматике естественного языка, а именно языковое выражение или соединение слов, имеющее самостоятельный смысл. В процессе рассуждения (не только в математике), с применением частицы не или соединяя их с помощью союзов и, или, если…, то, если и только если и др., обозначающих определенные логические связи между предложениями, из одних предложений формируются другие.

Для выяснения структуры сконструированного таким образом сложного предложения чаще представляется удобным исходные предложения обозначать буквами, отвлекаясь от их конкретного содержания.

Одна из существенных особенностей математического языка состоит в применении переменных различных типов, благодаря чему появляется такая способность языка, как способность выражать абстрактные формы, которые могут заполняться конкретным содержанием. Понятие это по существу всем нам хорошо знакомо – с ним мы часто встечаемся при заполнении различных стандартных бланков.

Под переменной понимается символ, вместо которого можно подставить имена элементов некоторого множества.

Предметы, имена которых разрешается подставить вместо переменной, называются ее значениями, а множество этих предметов – областью значений этой переменной.

ВЫСКАЗЫВАНИЯ. ПРЕДИКАТЫ

В математике мы имеем дело с различными высказываниями. Например, А  {число 100 делится на 10}, В  {число 12 делится на 5}, С  {два меньше шести}, М  {число 3 является единственным корнем уравнения x²–9=0}, K  {все девушки – блондинки}, T  {существуют двугорбые верблюды},

Очевидно, в некоторых из этих высказываний утверждается нечто правильное – такие высказывания называются истинными. В других же утверждается нечто неверное – такие высказывания называются ложными. Принято истинные высказывания обозначать с помощью символа И или цифры 1, ложные – с помощью Л или цифры 0. Оценим истинность наших высказываний.

Высказывание	А	В	С	М	K	T
Его истинность	И	Л	И	Л	Л	И

Повествовательное предложение, относительно которого имеет смысл говорить, что его содержание истинно или ложно, называют высказыванием. Принято обозначать высказывания большимим латинскими буквами, например А, В, С и т.д.

Задание: Приведите пример высказываний, связанных с вашей специальностью.

Всякое высказывание является предложением и может быть выражено словами. В математике при записи высказываний используются не только слова и буквы, но и специальные математические знаки. Каждый знак заменяет собой слово (или даже несколько слов). Используются знаки для сокращения записи. Например, высказывание С можно с помощью знаков записать следующим образом: 2 < 6.

Как уже было отмечено, каждое высказывание является предложением. Но не всякое предложение является высказыванием. Например,

1) Число ,000001 очень мало.

2) Сколько будет 18 + 76?

3) x < 6.

4) x – 4 = 7.

5) Как пройти в метро?

6) С праздником!

Первое из этих предложений не является высказыванием, так как оно не имеет точного смысла, и мы не можем сказать истинно оно или ложно. Один скажет, что это число на самом деле очень мало, а другой, например, с точки зрения фармацевта, скажет, что это число велико. Второе, пятое и шестое предложения вообще ничего не утверждают, а содержат либо знак вопроса, либо восклицательный знак. Бессмысленно говорить истинно каждое из них или ложно. Третье и четвертое предложение содержат букву x. При одних значениях x получается истинное высказывание, при других – ложное. Значит, в таком виде (пока не сказано, чему равен x) мы не можем сказать, истину или ложь выражают эти предложения. В математике таким предложениям отводится особая роль, и о них мы поговорим чуть ниже.

Замечание: не о всяком высказывании можно сразу ответить истинно оно или ложно. Когда мы говорим о возможности оценить предложение на истинность или ложность, то мы имеем в в виду принципиальную возможность решить этот вопрос. Например, E ≡ {число (126⁵⁴²² + 21⁷⁸⁶⁴)⁷⁸⁰⁹ + (124⁸⁷⁶² – 438¹²²)³⁴⁴⁸ + 8 является составным}, здесь вопрос об истинности принципиально может быть решен, но требует огромного количества вычислений. Но в силу того, что вопрос об истинности принципиально может быть решен, данное предложение Е является высказыванием.

Выводы:

1. Всякое высказывание является либо истинным, либо ложным (закон исключения третьего).

2. Никакое высказывание не может быть одновременно истинным и ложным (закон противоречия).

3. Предложение, о котором невозможно однозначно решить вопрос, истинно оно или ложно, высказыванием не является.

Из заданных высказываний А, В можно составить новые высказывания, используя связки «и», «или», «если…, то» «тогда и только тогда, когда», а также частицу «не». Полученные высказывания называют составными или сложными, а входящие в них высказывания А и В – элементарными высказываниями. Таким образом, высказывание называется составным (сложным) если оно допускает расчленение на другие высказывания. И если никакая часть высказывания сама уже не является высказыванием (или по крайней мере не рассматривается как таковое), то его называют элементарным.

Два составных высказывания А и В называют равносильными (эквивалентными), если они одновременно истинны или одновременно ложны при любых предположениях об истинности входящих в них элементарных высказываний. Записывают: А = В.

Кроме высказываний в логике рассматриваются предикаты (неопределенные высказывания). Предикат – это как бы высказывание, содержащее неизвестную (или несколько неизвестных). Поясним это на примерах.

Рассмотрим следующее предложение, содержащее переменную n: «n делится на 3». Обозначим это предложение через A(n). Предложение A(n) высказыванием не является: о его истинности сейчас мы ничего сказать не можем. Но при подстановке вместо n конкретных чисел, данное предложение становится высказыванием. Например, при n = 1 получается высказывание A(1), которое словами выражается так: «1 делится на 3». Это высказывание ложно. При подстановке вместо n числа 27, получаем высказывание A(27), которое читается так: «27 делится на 3» и является истинным и т.д. (см. таблицу)

A(1)	A(2)	A(3)	A(4)	A(5)	A(6)	A(7)	A(8)	A(9)	A(10)	A(11)	…
Л	Л	И	Л	Л	И	Л	Л	И	Л	Л	…

Таким образом, A(n) представляет собой предложение, которое при каждом конкретном n превращается в некоторое высказывание. Такие предложения в математике называют предикатами (неопределенными высказываниями). В данном случае предикат A(n) содержит переменную n, которая может принимать значения из множества натуральных чисел N. Поэтому говорят, что предикат A(n) задан на множестве натуральных чисел.

Замечание: слово «предикат» в переводе с латинского означает «сказуемое» (оно употребляется также в немецком, английском и других языках). Например, в рассмотренном предложении A(n) в роли подлежащего выступает буква n, а вся остальная часть предложения представляет собой сказуемое «делится» с подчиненными ему словами. Подставляя вместо n то или иное подлежащее (в нашем случае числительные 1, 27 и т. д.), мы получаем некоторые высказывания.

Аристотель ограничился в своей логике рассмотрением предикатов от одной переменной. Но после работ Буля в рассмотрение вошли предикаты и от нескольких переменных.

Рассмотрим пример предиката от двух переменных : {Писатель B написал книгу c}. Если вместо В и с подставим какие-либо конкретные значения, то получим высказывание. Например, пусть В – А. П. Чехов, с – «Война и мир», получим ложное высказывание {Писатель А. П. Чехов написал книгу «Война и мир»}. А при подстановке В – Л. Н. Толстой, с – «Война и мир» получаем истинное высказывание {Писатель Л. Н. Толстой написал книгу «Война и мир»}.

Другой пример. Рассмотрим предложения, в которых под x и y понимаются произвольные натуральные числа:

А(x,y) ≡ {x ≥ y},

В(x,y) ≡ {x + y = 12},

С(x,y) ≡ {x делится на y},

D(x,y) ≡ {x + y – число, кратное 9}

Имея предложения в таком виде, мы ничего не можем сказать об их истинности или ложности. Однако, при подстановке конкретных значений, каждое из них преобразовывается в высказывание – для одних пар (x, y) истинное, для других – ложное. Например, А(3, 7) ≡ {3 ≥ 7} ложное высказывание, А(10, 7) ≡ {10 ≥ 7} истинное высказывание, В(19, 2) ≡ {19 + 2 = 12} ложное высказывание, В(9, 3) ≡ {9 + 3 = 12} истинное высказывание, С(629, 25) ≡ {629 делится на 25} ложное высказывание, С(625, 25) ≡ {625 делится на 25} истинное высказывание, D(2, 26) ≡ {2 + 26 – число, кратное 9} ложное высказывание, D(2, 16) ≡ {2 + 16 – число, кратное 9} истинное высказывание.

Задание: Приведите примеры различных предикатов, связанных с вашей специальностью.

Можно рассматривать предикаты от трех и более переменных.

Рассмотрим интерпретацию предикатов на языке теории множеств. Рассмотренный нами ранее в качестве примера предикат A(n) задан на множестве N всех натуральных чисел. Множество A  N, состоящее из чисел, делящихся на 3: {3,6,9,12,15,18,…}, представляет собой множество всех тех значений n, для которых A(n) превращается в истинное высказывание. Его дополнение cA = N \ A представляет собой множество всех тех значений n, при подстановке которых рассматриваемый предикат превращается в ложное высказывание. Например, 81 А, так как А(81) – истинное высказывание (81 делится на 3), а 82 сА, потому что А(82) – ложное высказывание (т.к. 82 не делится на 3).

Вообще, если задано некоторое универсальное множество U, на котором определен предикат B(x), то с точки зрения теории множеств это означает, что выделено некоторое подмножество В U, состоящее из всех x  U, при подстановке которых B(x) превращается в истинное высказывание. Его дополнение сВ состоит из всех x  U, при подстановке которых B(x) превращается в ложное высказывание. Множество В называется множеством истинности предиката B(x).

Множества истинности предикатов можно обозначать с помощью фигурных скобок. Например, запись означает, что А есть множество всех тех x N, для которых имеет место A(x), т.е. множество истинности предиката. Более подробно: A = {x  N: x делится на 3}.

Упражнения:

1. Прочтите словами следующие высказывания, записанные знаками; 5  3, 10 + 2 = 14, 4 – 1  7, 4⁴ = 256, 5³  125 Какие из этих высказываний истинные, какие ложные?

2. Рассмотрите следующие два высказывания: С  {существуют четные простые числа} H  {существуют нечетные простые числа} Определите их истинность. Является ли высказывание H отрицанием высказывания С? Составьте отрицания к обоим высказываниям.

3. Является ли высказыванием утверждение «У любой собаки четыре глаза»?

4. Найдите множество истинности высказывания: сумму в n рублей можно уплатить купюрами в 50 и 100 рублей.

КВАНТОРЫ ОБЩНОСТИ И СУЩЕСТВОВАНИЯ.

Рассмотрим высказывания: С ≡ {через любые две точки проходит едиственная прямая}, D≡{для любых трех точек А, В, С сумма длин отрезков АВ и ВС не меньше длины отрезка АС}.

В них используются выражения «любые две точки», «для любых трех точек». Часто приходится формулировать и другие высказывания, в которых используются слова «все», «всякий», «каждый», «любой» и т.п. в математике принято вместо этих слов при записи использовать знак (перевернутая буква А английского слова All – все), который называется знаком общности или квантором общности.

Рассмотрим два утверждения:

1) Сумма углов треугольника АВС равна 180^º. 2) В треугольнике АВС угол А прямой.

Чтобы подчеркнуть общность первого утверждения, т.е. его справедливость для любого треугольника АВС, используется знак : ( АВС) (А+В+С=180^º). Читается «Для любого треугольника АВС сумма углов А, В, С равна 180^º». Это истинное высказывание.

Второе утверждение такой общностью не обладает: если перед этим утверждением записать ( АВС), то получается ложное высказывание, т.к. кроме прямоугольных треугольников существуют треугольники остроугольные и тупоугольные.

Вернемся к приведенному ранее высказыванию. D ≡ {для любых трех точек А, В, С сумма длин отрезков АВ и ВС не меньше длины отрезка АС}. В нем используется предикат АВ+ВС ≥ АС, в котором имеются три переменные: точки А, В, С, т.е. это предикат от трех переменных. Высказывание D можно записать так: ( т. А, В, С) (АВ+ ВС ≥ АС). Знак общности в этом случае показывает, что неравенство треугольника справедливо для любых трех точек А, В, С. Символ «т.» – сокращение слова «точка».

Если к предикату, содержащему некоторую переменную, например, x, добавить слева запись ( x) или, как говорят, «навесить» на переменную x квантор общности, то получится некоторое высказывание (истинное или ложное).

Возьмем предикат, определенный на множестве Н всех животных: А(х) = {х имеет две ноги}.

Навесив на переменную квантор общности, получаем высказывание: ( хН) А(х), т.е. словами: «любое животное х имеет две ноги». Мы получили ложное высказывание.

Кроме квантора общности в математике часто применяется и другой квантор – квантор существования.

Часто приходится формулировать высказывания, в которых используются слова: хотя бы один, найдется, существует и т.д. В математике принято при записи вместо этих слов использовать знак  (перевернутая буква Е английского слова Exists – «существует»).

В качестве примере рассмотрим три предиката, заданные на множестве всех треугольников:

А(Т) ≡ {в треугольнике Т сумма величин углов равна 180^º}; В(Т) ≡ {один из углов треугольника Т – прямой}; С(Т) ≡ {два угла треугольника Т – прямые}.

Предикат А(Т) для всякого конкретного треугольника Т превращается в истинное высказывание. Другими словами, высказывание ( Т) А(Т) истинно (т.к. в любом треугольнике сумма углов 180^º).

Предикат В(Т) не для всякого конкретного треугольника Т превращается в истинное высказывание (как мы уже отмечали ранее, кроме прямоугольных существуют еще остроугольные и тупоугольные треугольники). Например, рассмотрим треугольники Т₁ и Т₂, изображенные на рисунке.

Т огда, В(Т₁) – ложное высказывание, В(Т₂) – истинное высказывание.

Поэтому мы не можем утверждать, что для любого Т имеет место В(Т) – не в любом треугольнике один из углов прямой. Другими словами, высказывание ( Т) В(Т) ложно. Однако, существуют такие треугольники, для которых В(Т) истинно, например Т₂, т.е. В(Т₂) – истинно. И здесь на помощь приходит квантор существования . Факт существования треугольников с прямым углом записывается с помощью квантора существования следующим образом: ( Т) В(Т). Читаем: существует Т, для которого справедливо В(Т), т.е. существует треугольник у которого один из углов прямой.

Предикат С(Т) ни для какого треугольника Т не превращается в истинное высказывание (во всяком случае, в Евклидовой геометрии).

Итак, кванторы (общности, существования) превращают предикат в высказывание. Причем, квантор общности из словесных формулировок заменяет слова: всякий, каждый, любой, все. Квантор существования  из словесных формулировок заменяет слова: существует, найдется, какой-нибудь, хотя бы один.

Упражнения.

1. Используя кванторы, запишите высказывание: «Уравнение ax = b имеет решение». Найдите множество истиности этого высказывания.

2. Используя кванторы, запишите высказывание: «Уравнение ax = b имеет положительный корень». Найдите множество истиности этого высказывания.

3. Используя кванторы, запишите высказывание: «Существует целое число, которое делится на любое другое целое число, отличное от нуля». Истинно ли это высказывание?

4. Запишите с помощью знаков ,  следующие высказывания: 4.1. Каково бы ни было натуральное число x, найдется такое натуральное число y, что (x+y) – простое число. 4.2. Каково бы ни было натуральное число y, среди натуральных чисел найдется такое число x, что (x+y) – четное число. 4.3. Каково бы ни было натуральное число x, можно подобрать такое натуральное число y, что x² +y² < 100.

ЛОГИЧЕСКИЕ ОПЕРАЦИИ.

ОТРИЦАНИЕ.

Из всякого высказывания А можно получить новое высказывание, отрицая его, т.е. утверждая, что высказывание А не имеет места, не выполняется. Отрицание высказывания А обозначается символом А.Запись А читается как «отрицание высказывания А» или «не А».

Отрицание высказывания можно получить, сказав: «утверждение А не имеет места» или «А не выполняется». В ряде случаев отрицание можно получить еще проще. Например, если высказывание выражается простым предложением с одним сказуемым, то для получения отрицания нужно лишь добавить к сказуемому частицу «не».

Приведем примеры высказываний и их отрицаний.

А ≡ {Москва – столица России}, А ≡ {Москва не является столицей России} или {Неверно, что Москва – столица России}.

В ≡ {число 17 делится на 7}, В ≡ {число 17 не делится на 7}.

С ≡ {три больше пяти}, т.е. {3  5}, С ≡ {три не больше пяти} или {3  5}.

D ≡ {тридцать один – простое число}, D ≡ {тридцать один – не простое число}.

Е ≡ {разность чисел 18 и 2 равна 10}, т.е. {18 – 2 = 10}, Е ≡ {разность чисел 18 и 2 не равна 10}, т.е. {18 – 2  10}.

Но такой прием (добавить к сказуемому частицу «не») для образования отрицания неприменим, если само высказывание уже является отрицательным, т.е. уже содержит частицу «не» перед сказуемым. В качестве примера рассмотрим высказывание

К ≡ {11 не делится на 2}, Для образования отрицания К мы не можем добавить еще одно отрицание к сказуемому (т.е. не можем сказать: «11 не не делится на 2»). Поэтому отрицание формулируем так: К ≡ {высказывание «11 не делится на 2» места не имеет}. Но это утверждение означает, что 11 делится на 2, тогда К можно сформулировать следующим образом: К ≡ {11 делится на 2}.

Таким образом, если в некотором высказывании перед сказуемым уже стоит отрицательная частица «не», то для образования отрицания достаточно выбросить эту частицу.

Оценим данные и полученные высказывания на истиность, для наглядности составим таблицу:

А	А	ВвВ	В	С
1	0	0	1	0

С	D	D	E	E
1	1	0	0	1

G	G	I	I	К	К
1	0	1	0	1	0

Замечаем, если некоторое высказывание истинно, то его отрицание ложно, и наоборот. Это утверждение удобно записать в виде таблицы истинности:

А	А
И (1)	Л (0)
Л (0)	И (1)

Это положение математической логики, из двух высказываний, одно из которых является отрицанием другого, одно истинно, а другое ложно, называют законом исключения третьего. Иными словами, либо А, либо не А; третьего быть не может.

Замечание: Операцию отрицания можно применять не только к высказываниям, но и к предикатам. Рассмотрим предикат А(Т), заданный на множестве всех треугольников: «треугольник Т – равносторонний». Отрицание А(Т) тоже представляет собой предикат: «треугольник Т не является равносторонним».

Пусть А – произвольное высказывание. Его отрицание А также является высказыванием. Значит можно рассматривать и его отрицание, т.е. высказывание А. Оно называется двойным отрицанием высказывания А. Его можно сформулировать словами так: утверждение о том, что высказывание А не выполняется места не имеет. Но по смыслу это совпадает с самим высказыванием А.

Таким образом, двойное отрицание А истинно в том и только в том случае, если истинно само высказывание А (т.е. если А истинно, то и А истинно, а если А ложно, то и А ложно). Это правило называется законом отрицания отрицания.

Справедливости ради надо отметить, что в математической логике существует школа интуиционистов, которые не признают абсолютной истинности закона исключения третьего, т.е. считают неправомочной (по меньшей мере не очевидной) возможность отождествлять двойное отрицание А с исходным высказыванием А. Из наших соотечественников наиболее ярким представителем этой школы является А.А. Марков.

Мы же с вами придерживаемся формальной логики и будем изучать логические операции в ее рамках.

Как мы уже отмечали, если высказывание выражено простым предложением с одним сказуемым, то для образования его отрицания достаточно добавить «не» к сказуемому (а если частица «не» стояла перед сказуемым, то для образования отрицания достаточно эту частицу опустить).

Однако такой простой прием образования отрицания неприемлем в том случае, если высказывание содержит кванторы общности или существования ,  (или слов, их заменяющих).

Убедимся на примере. Для чего рассмотрим высказывание: S ≡ {каждое из чисел a, b, c делится на 5}, которое является ложным. Если составить его отрицание согласно выше обозначенному приему (добавить частицу «не» перед сказуемым), то получим следующее высказывание: S₁ ≡ {каждое из чисел a, b, c не делится на 5}, которое также является ложным, и высказывание S₁ не является отрицанием высказывания S. На самом деле, отрицание высказывания S формулируется так: S ≡ {не каждое из чисел a, b, c делится на 5}.

Чтобы убедиться в сложности образования отрицания для высказываний, содержащих кванторы, рассмотрим древний софизм (софизм – это…). В нем говорится о лжецах (говорят всегда неправду), и правдивых людях (не лжецы), которые всегда говорят правду. Итак, вот этот софизм.

Один критянин (житель острова Крит) утверждал, что все критяне лжецы. Но он сам критянин и потому лжец. Значит, он сказал неправду., т.е. все критяне не лжецы, а правдивые люди. Но тогда он (поскольку он – критянин) тоже правдивый человек. Значит, он все же сказал правду, тогда все критяне лжецы. Но это значит, что и он лжец, т.е. он сказал неправду, а потому критяне правдивы…

Чтобы разорвать этот замкнутый круг, необходимо детально рассмотреть взаимодействие отрицания с кванторами.

Рассмотрим еще примеры высказываний, содержащих кванторы (или равнозначные им слова).

F ≡ {в любом треугольнике АВС величины углов А и В равны}. Если просто добавить «не» к сказуемому, то получится: F₁ ≡ {в любом треугольнике АВС величины углов А и В не равны}. Поскольку оба высказывания являются ложными, то F₁ не является отрицанием F. Отрицанием для F будет следующее высказывание: F ≡ {не в любом треугольнике АВС величины углов А и В равны}, т.е. необходимо отрицание «не» поставить перед всем высказыванием. Запишем это высказывание и его отрицание знаками. F ≡ ( АВС) (А = В), F ≡   ( АВС) (А = В). Высказыввание:  F ≡ {не в любом треугольнике АВС величины углов А и В равны} равнозначно тому, что найдется (существует) АВС, в котором не имеет места соотношение А = В: F ≡ (АВС) (А = В).

Подведем итог: если высказывание начинается со слов «все», «каждый», «любой» и т.п., то для получения отрицания надо либо, ничего не меняя, поставить отрицание «не» перед этими словами, либо же поставить отрицание «не» после этих слов, но тогда эти слова необходимо заменить на «хотя бы один», «найдется», «существует» и т.п., т.е. чтобы образовать отрицание высказывания, начинающегося знаком , можно либо поставить знак перед всем высказыванием, либо заменить знак  на  и при этом поставить знак перед остальной частью высказывания. Аналогично поступаем если высказывание начинается со слов «хотя бы один», «найдется», «существует» и т.п. или квантора .

Если условимся считать знаки  и  противоположными, то правило составления отрицания можно сформулировать так:

Чтобы образовать отрицание высказывания, начинающегося одним из знаков  или , можно:

1. способ. Поставить знак   перед всем высказыванием; 2 способ. 2.1. заменить начальный квантор( или ) на противоположный, 2.2. поставить знак перед остальной частью высказывания.

Вернемся к рассмотренному ранее софизму. Обозначим через К множество всех критян, а через А(х) обозначим предикат «х – лжец». Тогда высказанное критянином утверждение можно записать так: ( х  К) А(х).

Первый вывод, указанный в софизме, верный: если все критяне лжецы, то он сам лжец, т.е. он сказал неправду. Значит, написанное высказывание ложно, т.е. истинным является его отрицание ( х  К) А(х). Или в словесной формулировке это звучит так: не все критяне лжецы, т.е. существует (по крайней мере один) критянин, не являющийся лжецом: ( х  К) А(х).

Итак, существует критянин, являющийся правдивым человеком. Но это не значит, что все критяне правдивы. Поэтому ниоткуда не следует, что тот критянин, который высказал утверждение, правдив. Т.е. мы не вправе заключить, что он сказал правду. На этом и обрывается приведенное в софизме рассуждение, т.е. никакого замкнутого круга не получается.

Интерес представляют контрпримеры при решении вопроса о том, верно ли некоторое утверждение, содержащее кванторы общности или существования ( или ).

Упражнения:

1. Рассмотрите следующие два высказывания: С  {существуют четные простые числа} H  {существуют нечетные простые числа} Является ли высказывание H отрицанием высказывания С? Составьте отрицания к обоим высказываниям.

2. Постройте отрицание высказывания: «Каждому овощу свое время».

3. Постройте отрицание высказывания: «Среди ста трехзначных чисел найдутся два равных». Какое из этих высказываний истинно?

4. Постройте отрицание высказывания: «не существует ромба, который может быть вписан в окружность». Какое из этих высказываний истинно?

5. Постройте отрицание высказывания: «Во всяком треугольнике медианы пересекаются в одной точке». Какое из этих высказываний истинно?

Конъюнкция.

Часто приходится иметь дело с высказываниями, в которых выполняются два каких-либо свойства. Например высказывание: существуют равнобедренные прямоугольные треугольники. Это высказывание означает, что существует АВС, который одновременно обладает двумя свойствами: угол С – прямой и АС = ВС.

В математике одновременное выполнение двух свойств принято называть конъюнкцией этих свойств и обозначать знаком (читается «и»). Учитывая данный факт выше приведенное высказывание можно записать так: (  АВС) ((= 90) (АС = ВС)).

В качестве другого примера использования конъюнкции можно привести пример определения пересечения множеств. По определению, элемент принадлежит пересечению множеств А и В, если он принадлежит и множеству А, и множеству В, т.е. А  В = {х: (х  А) (х  В)}. В данном случае фигурные скобки означают слово «множество», а двоеточие – словосочетание «для которых» (т.е. двоеточие поясняет, какие х надо взять).

Аналогично для определения разности двух множеств. По определению, элемент принадлежит разности множеств А и В, если он принадлежит множеству А, и не принадлежит множеству В, т.е. А \ В = {х: (х  А) (х  В)}.

Высказывание А В истинно, если истинны оба высказывания А, В и ложно во всех остальных случаях.

Для операции конъюнкции справедлива следующая таблица истинности:

А	В	А В
И (1)	И (1)	И (1)
И (1)	Л (0)	Л (0)
Л (0)	И (1)	Л (0)
Л (0)	Л (0)	Л (0)

Свойства конъюнкции:

1. Коммуникативность: А В = В А, для любых двух высказываний А и В.

2. Ассоциативность: (А В) С = А (В С), для любых А, В, С.

3. Конъюнкция А А тождественно ложна, т.е. А А = Л.

дизъюнкция.

Кроме операции конъюнкции в математике часто используется операция дизъюнкция, обозначается символом , читается «или». Знак не совсем точно передается союзом «или», которым мы пользуемся в обычной речи. Для примера рассмотрим фразу «Я уезжаю, но за рукописью зайдет мой муж или дочь». В данном случае союз «или» понимается в смысле «либо-либо», т.е. зайдет либо муж, либо дочь; возможность, что они зайдут вместе не предусматривается. Т.е. в обычной речи союз «или» имеет разделительный оттенок. В математической же логике операция не имеет разделительного смысла, т.е. А В означает, что либо имеет место А (но не В), либо имеет место В (но не А), либо же (и в этом отличие) имеют место А и В вместе. Для нашего примера это означает, что за рукописью может зайти либо муж, либо дочь, либо они могут зайти вместе.

Д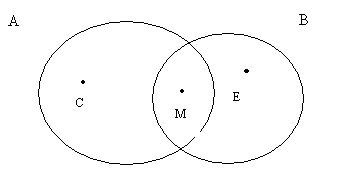 ругим наглядным примером дизъюнкции высказываний служит операция объединения множеств. Используя определение объединения множеств, можно сделать вывод. Если элемент х принадлежит объединению множеств А и В, то имеет место один из трех случаев: 1) либо х  А, но х  В (точка С); 2) либо х  В, но х  А (точка Е); 3) либо х  А и х  В (точка М).

Запись А  В = {х: (х  А) (х  В)} и означает, что имеет место один из этих случаев.

Высказывание А В ложно только в том случае, если ложны оба высказывания А и В.

Для операции дизъюнкции справедлива следующая таблица истинности:

А	В	А В
И (1)	И (1)	И (1)
И (1)	Л (0)	И (1)
Л (0)	И (1)	И (1)
Л (0)	Л (0)	Л (0)

Свойства дизъюнкции:

1. Коммуникативность: А В = В А, для любых двух высказываний А и В.

2. Ассоциативность: (А В) С = А (В С), для любых А, В, С.

3. Конъюнкция А А тождественно истинна, т.е. А А = И.

4. Дистрибутивность: 4.1. (А   В)   С = (А   С)   (В   С), для любых А, В, С; 4.2. (А   В)   С = (А   С)   (В   С), для любых А, В, С.

Упражнения.

1. Что можно сказать об истинности высказывания ( А   В  С)   А, если А – ложное высказывание, а В и С – истинные? 2. Пусть А – истинное высказывание, а В и С – ложные. Будет ли истинным высказывание (А   В)   ( В   С)   ( С   А)? ( В   А)   ( С   А)? 3. При каком условии высказывания А   (В   С) и ( А   С)   (А   В) одновременно истинны или ложны? 4. Составьте таблицу истинности для формулы: 4.1. А   (В   С), 4.2. А  (В   С).

5. Докажите следующее равенство (для всех значений А и В): 5.1. (А   В)   С = А   (В   С), 5.2. (А   В)   С = (А   С)   (В   С), 5.3. (А   С)   ( В   С) = (А   В)   С.

6. Покажите, что высказывания А и (А   В)   (А     В) всегда одновременно истинны или ложны.

ИМПЛИКАЦИЯ

Пусть А и В – два элементарных высказывания. Импликацией данных высказываний называется высказывание «Если А, то В» и обозначается А  В. Например,

Высказывание А: А  {Сегодня воскресенье}. Высказывание В: В  {У меня выходной}. Высказывание А  В А  В  {Если сегодня воскресенье, то у меня выходной}.

Условились считать, импликация двух высказываний ложна тогда и только тогда, когда первое высказывание (его называют «посылка») – истинно, а второе (его называют «заключение») ложно. Во всех остальных случаях импликация истинна.

А	В	А  В
И (1)	И (1)	И (1)
И (1)	Л (0)	Л (0)
Л (0)	И (1)	И (1)
Л (0)	Л (0)	И (1)

Упражнения.

1. Пусть А – высказывание: «число делится на 2», В – «число делится на 7», С – «число делится на 14». Какие из следующих высказываний истинные: 1.1. С  А   В, 1.2. А   В  С, 1.3. С   В   А?

2. Составьте таблицу истинности для формулы: 2.1. А   (В  С), 2.2. А   (В   С), 2.3. А   ( В  С).

3. Докажите следующее равенство: 3.1. (А  В) = ( А   В), 3.2. (А  В) = ( В   А).

4. Даны следующие высказывания: А  {Сегодня суббота}, В  {Сегодня пасмурно}, С  {Я буду читать книгу}. Определите их истинность. Составьте таблицу истинности для указанных формул и определите их истинность: 4.1. С  (А   В), 4.2. С  (А   В), 4.3. С   (А   В).

ЭКВИВАЛЕНЦИЯ

Пусть А и В – два элементарных высказывания. Эквиваленцией данных высказываний называется высказывание «А тогда и только тогда, когда В» и обозначается А  В. Рассмотрим пример: Высказывание А: А  {Я не иду в университет}. Высказывание В: В  {Сегодня воскресенье}. Высказывание А  В А  В  {Я не иду в университет тогда и только тогда, когда вокресенье}.

Эквиваленция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или одновременно ложны. В остальных случаях эквиваленция ложна.

А	В	А  В
И (1)	И (1)	И (1)
И (1)	Л (0)	Л (0)
Л (0)	И (1)	Л (0)
Л (0)	Л (0)	И (1)

Составные высказывания, истинные при любых предположениях о входящих в них элементарных высказываниях, называют тавтологиями. Например, А   В  В   А и А   В  В   А – тавтологии.

Замечание: логические операции делятся по старшинству, что позволяет избегать большое количество скобок при записи составных высказываний. Наибольший приоритет имеет отрицание, затем конъюнкция и дизъюнкция, затем импликация, и самый низкий приоритет имеет эквиваленция.

При составлении таблиц истинности составных высказываний применяют следующее правило: перебирают все возможные варианты значений истинности элементарных высказываний, входящих в составное. Число таких вариантов (это и есть число строк таблицы истинности) равно 2ⁿ, где n – количество элементарных высказываний. Например, число строк таблицы истинности для формулы А   В  В   А равно 4 (т.к. рассматриваются два элементарных высказывания А и В, то 2²), а для формулы А   В   С равно 2³ = 8 (т.к. рассматриваются три элементарных высказывания А, В и С).

Упражнения.

1. Докажите следующую тавтологию: 1.1. А   В  В   А. 1.2. А   В  В   А. 1.3. (А   В)   В    А. 1.4. ((А   В)   А)   В. 1.5. (А   В)   А    В.

Задание: составьте таблицу соответствия между основными понятиями теории множеств и математической логики (заполните второй столбик).

Теория множеств	(Математическая) логика
Множество
Объединение
Пересечение
Дополнение
Универсальное множество
Пустое множество

Ответ:

Теория множеств	(Математическая) логика
Множество	Высказывание
Объединение	Дизъюнкция
Пересечение	Конъюнкция
Дополнение	Отрицание
Универсальное множество	Тавтология
Пустое множество	Противоречие

Примерный вариант решения задач.

1. Прочтите словами следующие высказывания, записанные знаками; 5  3, 10 + 2 = 14, 4 – 1  7, 4⁴ = 256, 5³  125 Какие из этих высказываний истинны, какие ложны?

Решение: Пять больше трех. И Сумма чисел 10 и 2 равна 14. Л Разность чисел 4 и 1 меньше 7. И Четыре в четвертой степени равно 256. И Пять в кубе неравно 125. Л

2. Рассмотрите следующие два высказывания: С  {существуют четные простые числа} H  {существуют нечетные простые числа} Определите их истинность. Является ли высказывание H отрицанием высказывания С? Составьте отрицания к обоим высказываниям.

Решение: По определению, число является простым, если имеет только два делителя (т.е. 1 само себя).

Определим истинность высказываний: высказывание С – истинное (т.к. число 2 – четное и простое), высказывание Н – истинное (например, число 7 – нечетное и простое). Высказывание Н не является отрицанием высказывания С (т.к. оба истинны). Составим отрицания данных высказываний: С  {не существуют четные простые числа}, H  {не существуют нечетные простые числа}.