38Определение программного управления. Источники динамических ошибок

При проектировании машины с программным управлением одной из главных задач является определение программного управления, обеспечивающего выполнение заданного программного движения. При этом в отличие от машин с программирующими механизмами решение кинематической задачи – задачи получения требуемого закона движения – тесно переплетается с задачей динамического анализа. С тем, как решается задача выбора программного управления, познакомимся на примере системы, схема которой приведена на рис. 9.1, б.

Составим уравнение движения механической системы

, (9.5)

где – угловое ускорение ротора двигателя, – приведенный момент инерции, – движущий момент. В связи с тем, что в системах с программным управлением возникают большие переменные инерционные силы, вызывающие значительные колебания движущего момента, при их исследовании должна использоваться динамическая характеристика двигателя. Полагаем, что используется двигатель постоянного тока с независимым возбуждением, принимаем эту характеристику в форме (8.4):

, (9.6)

где – параметры двигателя.

Пусть задан программный закон движения выходного звена . Из кинематических соотношений легко определить программный закон изменения :

. (9.7)

Подставляя в (9.5), определяем закон изменения движущего момента при программном движении:

. (9.8)

Далее определяем программное управление из уравнения (9.6):

. (9.9)

Введя в рассмотрение механическую постоянную времени , приводим выражение (9.9) к форме

. (9.10)

Казалось бы, задача определения программного управления решена: подав на вход двигателя напряжение , найденное из соотношения (9.10), мы должны получить требуемый закон программного движения. В действительности, однако, имеется ряд обстоятельств, приводящих к существенным отклонениям истинного закона движения от программного, а в ряде случаев – к невозможности осуществления программного движения.

Проблема реализуемости программного движения. Системы с программным управлением часто решают задачу перемещения рабочего органа из одного положения в другое при заданном законе движения. Предположим, что требуется осуществить перемещение рейки (рис. 9.1, б) на расстояние при изменении ускорения по закону, график которого показан на рис. 9.2. Здесь – время программного перемещения. Рейка должна проходить первую половину пути с постоянным ускорением . Если – величина требуемого перемещения, а начальная скорость равна нулю, то из условия равноускоренного движения имеем:

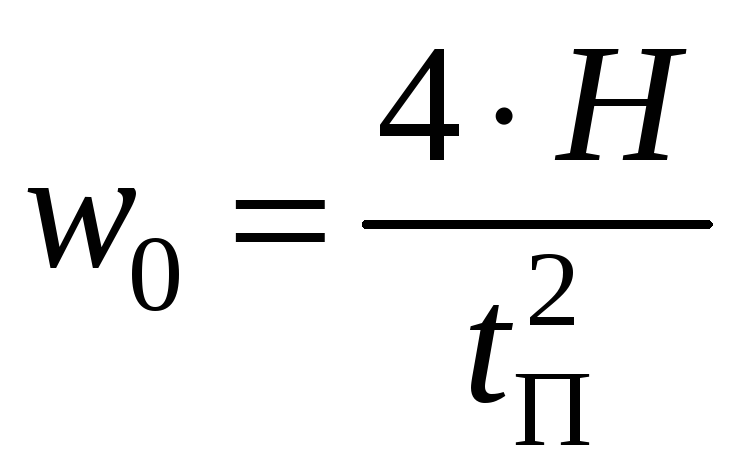, . (9.11)

Однако осуществить такое движение невозможно. Действительно, в начальный момент ускорение должно скачком измениться от нуля до . Для этого должно скачком измениться и угловое ускорение двигателя, то есть в этот момент должно принять «бесконечно большое» значение. Но тогда бесконечно большим должно быть в начальный момент и напряжение , что, естественно, невозможно.

Предположим теперь, что требуется осуществить периодическое возвратно-поступательное движение рабочего органа по закону

, (9.12)

где и – заданная амплитуда и частота. Подставляя (9.12) в (9.7), находим

. (9.13)

Подставив (9.13) в (9.10), находим программное управление:

. (9.14)

Таким образом, входное напряжение должно иметь амплитуду

. (9.15)

При заданном значении амплитуда возрастает с ростом ; при больших значениях она становится приблизительно пропорциональной . Поскольку амплитудные значения ограничены, в реальной системе возникают трудности при попытке осуществления высокочастотных колебаний рабочих органов машины. По этой причине в системе с программным управлением чаще реализуются сравнительно низкочастотные программные движения.

Влияние начальных условий. Подставив из (9.5) в (9.6), получим уравнение движения ротора двигателя в форме

(9.16)

или, после деления на ,

. (9.17)

Программное движение является частным решением этого уравнения при ; соответствующим вполне определенным начальным условиям. Общее решение линейного неоднородного уравнения (9.17) для записывается в форме

, (9.18)

где и – постоянные, определяемые из начальных условий; и – корни характеристического уравнения

,

откуда

. (9.19)

Легко убедиться, что корни (9.19) всегда либо отрицательные (при ), либо имеют отрицательную вещественную часть (при ). Отсюда следует, что первые два слагаемых в (9.18) стремятся к нулю и, следовательно,

при .

Таким образом, программное движение в системе устанавливается не сразу, а после окончания переходного процесса. При начальных условиях , , , то есть при движении системы из состояния покоя, получаем из (9.18):

, .

Для программного движения (9.13) получаем

, .

Из этих уравнений находим

, . (9.20)

Следовательно, скорость рабочего органа будет изменяться по закону

. (9.21)

Движение рабочего органа будет соответствовать программному только после затухания переходного процесса, отражаемого первым слагаемым в правой части выражения (9.21).

Неадекватность динамической модели системы. При определении программного управления мы исходили из динамической модели системы, описываемой уравнениями (9.5) и (9.6). В действительности эти уравнения лишь приближенно соответствуют реальной системе. Они не учитывают упругость реальных звеньев механической системы, отличия истинных значений параметров от номинальных и т.п. Все это приводит к отклонениям действительных движений системы от программных, т. е. к динамическим ошибкам.

Предположим, что в рассмотренном выше примере в качестве динамической модели двигателя выбирается его идеальная характеристика

. (9.22)

Оценим, какие динамические ошибки вызовет такое упрощение динамической модели. В соответствии с характеристикой (9.22) подставим в правую часть уравнения движения (9.17)

.

В результате получим

. (9.23)

Решение этого уравнения определит «действительный» закон изменения угловой скорости ротора (если считать действительной динамическую характеристику двигателя), а определит динамическую ошибку по скорости. Заменив в (9.23) на , получим уравнение для динамической ошибки:

. (9.24)

Общее решение этого уравнения складывается из общего решения однородного уравнения и частного решения, соответствующего установившейся динамической ошибке, устанавливающейся в системе после затухания переходного процесса. Очевидно, что общее решение даст динамическую ошибку, вызванную начальными условиями, а частное – динамическую ошибку, вызванную неточностью описания характеристики двигателя.

Легко видеть, что пренебрежение динамическими свойствами двигателя, связанное с использованием его идеальной характеристики, может приводить к очень большим динамическим ошибкам (в некоторых случаях амплитуда ошибки может превосходить амплитуду программной скорости).