35.Разбег с учетом статической характеристики двигателя

Изучение переходных процессов начнем с рассмотрения неуправляемого разбега машины. Предположим сначала, что может быть принята статическая характеристика двигателя. Поскольку разбег является неуправляемым, то . Предположим также, что приведенный момент инерции является постоянным, а приведенный момент сил сопротивления явно зависит от координаты ; тогда уравнение движения (8.17) принимает следующий вид:

. (8.56)

Пренебрежение переменными компонентами и обычно оказывается допустимым при исследовании переходных процессов.

Разбегу машины соответствует решение уравнения (8.56) при начальных условиях , . Обозначив , получим дифференциальное уравнение с разделяющимися переменными

. (8.57)

Решая его, находим

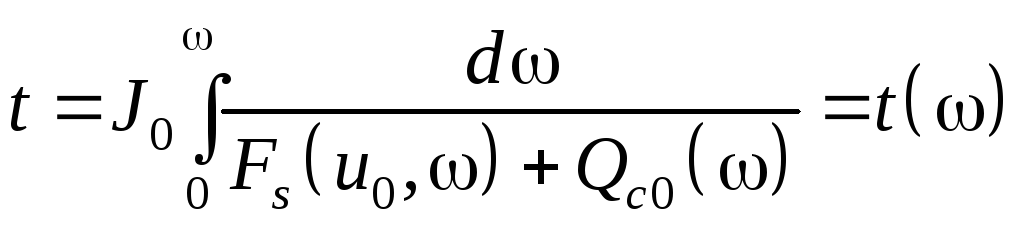. (8.58)

Обращением функции (8.58) получим зависимость . Время разбега можно определить как

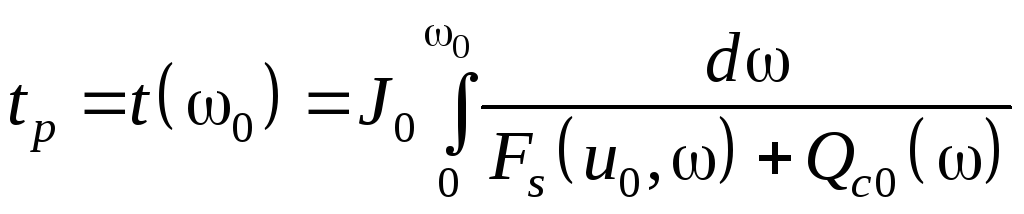. (8.59)

Однако легко показать, что интеграл этот расходится. Действительно, при знаменатель дроби, стоящей под интегралом, обращается в нуль ( поскольку – угловая скорость в установившемся движении, определяемая из уравнения (8.26)); поэтому интеграл является несобственным; он расходится, если

, (8.60)

что является условием устойчивости режима установившегося движения. Таким образом, теоретически время разбега бесконечно велико; поэтому условно за время разбега обычно принимается время достижения угловой скорости, близкой к , но меньшей ее. Чаще всего принимают, что

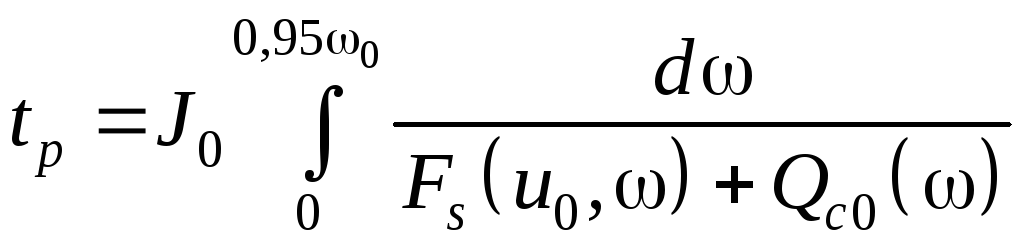. (8.61)

Из этой формулы видно, что время разбега пропорционально ; поэтому уменьшение момента инерции машины является одним из эффективных способов снижения времени переходного процесса.

Разбег при линейных характеристиках машины и двигателя

Пусть

, , (8.62)

где . Подставив (8.62) в (8.56), получим

.

Поделив оба слагаемых на и учитывая, что , имеем

. (8.63)

Общее решение этого уравнения записывается в виде

.

Из начального условия находим, что ; отсюда

. (8.64)

Полагая, что , , получаем

.

Таким образом, время разбега пропорционально величине .

Определение момента в передаточном механизме. Найдем момент , возникающий при разбеге в передаточном механизме. Составляя уравнение движения ротора двигателя, имеем

,

где – момент инерции ротора; поскольку

, , ,

получаем

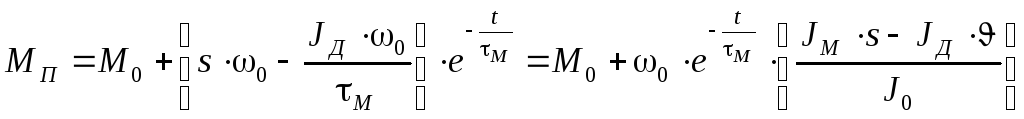, (8.65)

где .

Н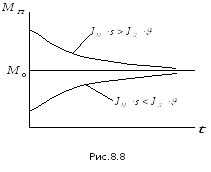а рис.8.8 построены возможные формы зависимости при разбеге. Очевидно, что при момент в передаточном механизме, возникающий в процессе разбега, превышает момент в установившемся режиме. Более предпочтительным является условие , при котором не превосходит в течение всего переходного процесса.

36Разбег с учетом динамической характеристики двигателя

Ограничимся рассмотрением системы с линейными характеристиками

(8.62), запишем уравнения движения машины в форме

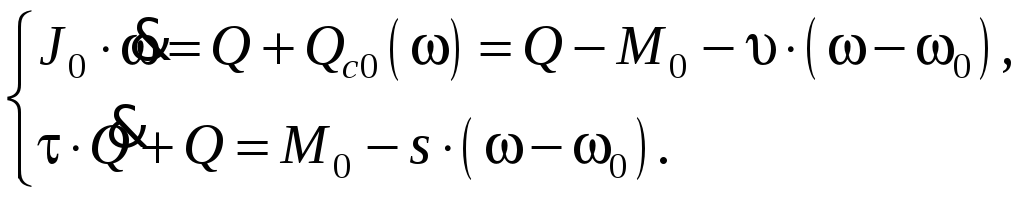(8.66)

Определим движущий момент из первого уравнения

.

Подставим это выражение во второе уравнение, получим

или, после упрощений,

.

В дальнейшем будем предполагать, что , и соответствующее слагаемое в коэффициенте при может быть отброшено.

Окончательно получаем

. (8.67)

Разбег описывается частным решением уравнения (8.67), соответствующим определенным начальным условиям. Одно из этих условий очевидно:

, . (8.68)

В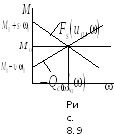торое начальное условие требует более подробных объяснений. Дело в том, что в момент включения двигателя движущий момент равен нулю, а момент сопротивления (рис. 8.9). Поэтому в этот момент времени разбег начаться не может. При неподвижном роторе начнется возрастание момента в соответствие с динамической характеристикой двигателя, в которой следует положить :

. (8.69)

Разбег начнется в тот момент, когда частное решение уравнения (8.69), соответствующее условию , достигнет величины, равной . Если отсчитывать время разбега от этого момента, то в качестве второго начального условия следует принять

, . (8.70)

Разыскивая общее решение линейного неоднородного дифференциального уравнения (8.67), найдем сначала корни его характеристического уравнения

.

Решая это уравнение, находим

. (8.71)

Далее необходимо рассмотреть два случая.

а). Если , то корни (8.71) являются вещественными и отрицательными. Решение уравнения (8.67) представляется в форме

.

Начальные условия (8.68) и (8.70) позволяют определить постоянные и :

, .

Разбег в этом случае является апериодическим процессом, при котором

. (8.72)

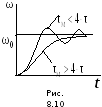
Примерная форма графика функции показана на рис. 8.10. Угловая скорость монотонно возрастает, стремясь к . Можно показать, что при всех в этом случае .

б). Если , то корни (8.71) являются комплексными сопряженными:

. (8.73)

Используя начальные условия, находим

. (8.74)

Разбег в этом случае оказывается затухающим колебательным процессом (рис. 8.10). Максимальное значение угловой скорости

достигается при . В этом случае угловая скорость в процессе разбега достигает значений, превосходящих , что часто является нежелательным.

Торможение машины

Рассмотрим процесс торможения машины, при котором двигатель выключается и включается тормоз, создающий дополнительный момент сопротивления , который будем считать постоянным по величине. В этом случае уравнение движения жесткой машины записывается в виде

. (8.75)

При линейной характеристике это уравнение принимает форму

или , (8.76)

где – постоянная времени при торможении. Решая уравнение (8.76) при начальном условии , находим

. (8.77)

Из условия , определяем время торможения

. (8.78)

Пусть – момент инерции ротора двигателя, а тормозной момент прикладывается непосредственно к ротору. Составим уравнение движения ротора в форме

,

где – момент в передаточном механизме, получаем

. (8.79)

При момент принимает наибольшее значение, равное . Обычно стремятся к тому, чтобы не превышал момента , действующего в передаче при установившемся движении. Тогда должно быть ; из этого условия можно выбрать величину тормозного момента.