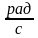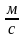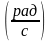Министерство образования Российской Федерации
Московский государственный технический университет имени н.Э. Баумана методические указания
по выполнению курсовой работы
«Колебания линейной системы с одной степенью свободы»
по курсу
«Механика сплошной среды»
Кафедра ИУ-10 «Защита информации»
Москва, 2010
Утверждено на заседании кафедры ИУ-10 «Защита информации» протокол №01/07 от 03.09.2007.
Курсовая работа по дисциплине “Механика сплошной среды” проводится на 3-м семестре.
Оглавление
Список рекомендуемой литературы 19
ВВЕДЕНИЕ
Цель курсовой работы: закрепить знания студентов, получаемые при изучении раздела «Теория колебаний» курса «Механика сплошной среды» и привить навыки самостоятельного исследования колебательных процессов в механических системах. Работа выполняется на 3 семестре.
В курсовой работе рассматриваются малые колебания механической системы с одной степенью свободы около положения устойчивого равновесия. Требуется составить дифференциальное уравнение движения и найти его решение при заданных начальных условиях. Для вынужденных колебаний провести исследование процесса перехода от начального возмущенного движения к установившимся вынужденным колебаниям и построить амплитудно-частотную и фазочастотную характеристики системы.
Механические системы, рассматриваемые в курсовой работе – плоские механизмы, расположенные в вертикальной плоскости и состоящие из твердых тел, нитей, демпферов и упругих элементов.
Линейно-вязкое
сопротивление при движении системы
возникает в демпфере, сила сопротивления
которого
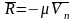 пропорциональна скорости движения
поршня
пропорциональна скорости движения
поршня
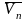 ,
,
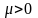 - коэффициент сопротивления демпфера;
массой демпфера можно пренебречь.
- коэффициент сопротивления демпфера;
массой демпфера можно пренебречь.
Силы и моменты сил воздействия упругих элементов на тела пропорциональны удлинению пружин или углу закручивания спиральных пружин.
Выполненная курсовая работа оформляется по ГОСТ 7.32-2001 и представляется на защиту комиссии в форме доклада с использованием средств мультимедийной аудитории.
ПРИМЕР ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ
Условие задачи
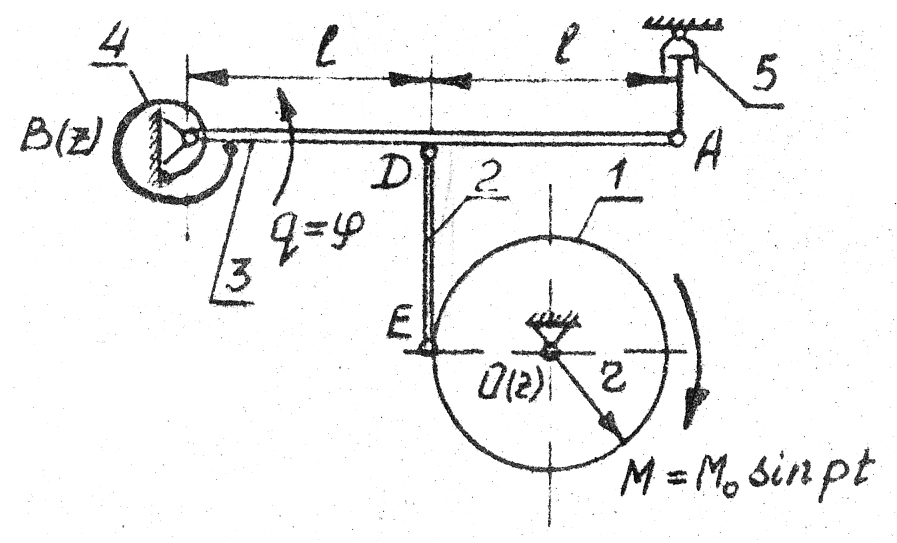
Рис.1
Пара
сил с моментом
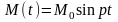 (М0=4
Н·м, p=15
рад/с) действует на маховик 1 (рис.1),
представляющий собой однородный диск
массой m1=4
кг и радиусом r=0,1м,
который может вращаться вокруг
горизонтальной оси O(z).
Стержень 2 массой m2=2кг
шарнирами E
и D
связан с однородным стержнем 3 массой
m3=3кг
и длиной 2l=0,6м.
(М0=4
Н·м, p=15
рад/с) действует на маховик 1 (рис.1),
представляющий собой однородный диск
массой m1=4
кг и радиусом r=0,1м,
который может вращаться вокруг
горизонтальной оси O(z).
Стержень 2 массой m2=2кг
шарнирами E
и D
связан с однородным стержнем 3 массой
m3=3кг
и длиной 2l=0,6м.
Вращению
стержня 3 вокруг горизонтальной оси
B(z)
препятствует спиральная пружина 4 с
коэффициентом жесткости С4=72
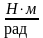 и демпфер 5 с коэффициентом сопротивления
и демпфер 5 с коэффициентом сопротивления
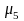 =40
=40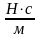 .
.
В
состоянии равновесия системы стержень
3 занимает горизонтальное положение. В
момент времени t=0
стержню 3 в положении равновесия была
сообщена начальная скорость
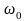 =1,23
рад/с.
=1,23
рад/с.
Решение
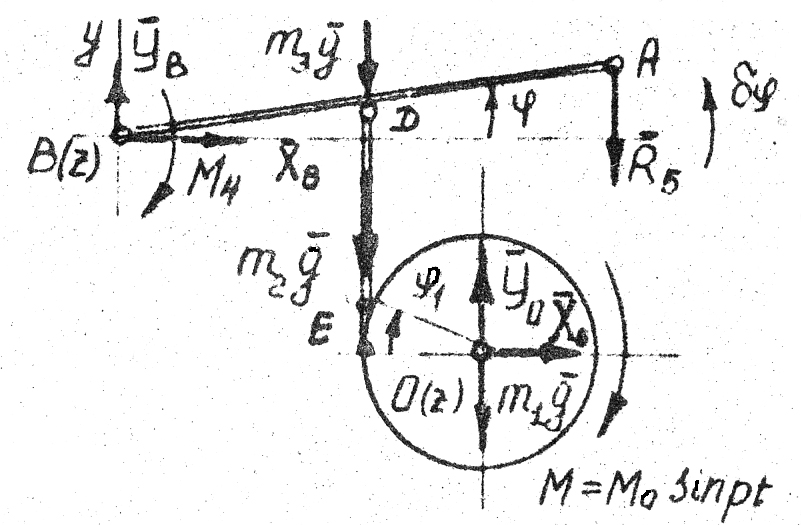
Рис.2
Составим
дифференциальное уравнения движения
системы, используя уравнения Лагранжа
II
рода, выбрав в качестве обобщенной
координаты q(t)
угол поворота
 стержня 3 вокруг оси B(z)
(рис.2) с положительным направлением
отсчета против хода часовой стрелки.
стержня 3 вокруг оси B(z)
(рис.2) с положительным направлением
отсчета против хода часовой стрелки.
В силу наложенных на систему связей
 ,
,
 ,
,
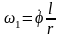 .
(1)
.
(1)
Кинетическая энергия системы
Т = Т1 + Т2 + Т3 ,
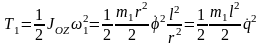 ;
;
при малых колебаниях звено 2 совершает мгновенно-поступательное движение, поэтому
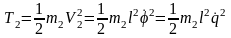 ;
;
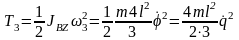 .
.
Тогда
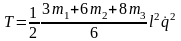 ,
(2)
,
(2)
Или
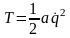 , где
, где
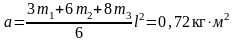 .
(3)
.
(3)
Обобщенную силу Q представим в виде
Q = QП + QФ + QВ (t) .
Учтем,
что горизонтальное положение равновесия
стержня 3 возможно лишь при статической
деформации пружины
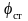 ,
которую определим из условия равновесия
системы
,
которую определим из условия равновесия
системы
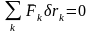 ,
,
или
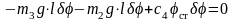 ,
,
тогда
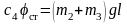 . (4)
. (4)
Запишем выражение, определяющее изменение потенциальной энергии системы при повороте стержня 3 на угол от положения статического равновесия
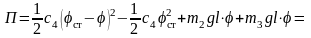
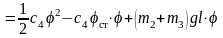 (5)
(5)
и,
в силу (4),
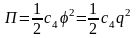 .
.
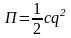 ,
с=с4=72
Н·м,
,
с=с4=72
Н·м,
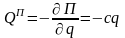 .
(6)
.
(6)
Диссипативная функция Рэлея
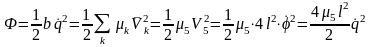 ,
,
откуда
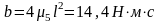 ;
;
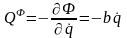 .
(7)
.
(7)
При
определении
 учтем, что возможные перемещения
учтем, что возможные перемещения
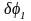 и
и
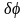 связаны между собой так же, как угловые
скорости маховика 1 и стержня 3:
связаны между собой так же, как угловые
скорости маховика 1 и стержня 3:
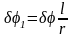 ,
(8)
,
(8)
тогда
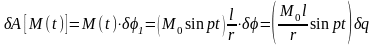 ,
,
и, следовательно,
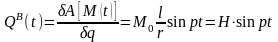 ,
,
где
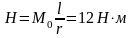 . (9)
. (9)
Дифференциальное уравнение движения системы с учетом (3), (6), (7) и (9) имеет вид
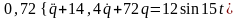 , (10)
, (10)
или в канонической форме
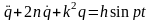 ,
,
где
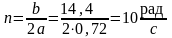 ,
,
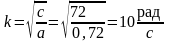 , (11)
, (11)
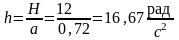 .
.
Имеем случай “критического” сопротивления n = k, поэтому общее решение однородного уравнения qо.о (t) запишем
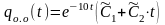 . (12)
. (12)
Справочно: При n>k – большое сопротивление – решение для qoo(t) имеет вид
где
qoo(t) имеет колебательный характер (описывает затухающие колебания) только при n<k – случай малого вязкого сопротивления. В этом случае qoo(t) может быть представлено одним из двух видов
или
где
|
Частное решение уравнения
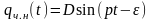 ,
,
где
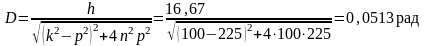 , (13)
, (13)
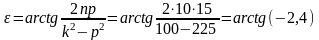 ,
,
поскольку ε меняется в пределах от 0 до π,
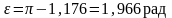 .
(14)
.
(14)
Общее решение уравнения (10) имеет вид
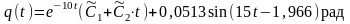 .
.
Постоянные
интегрирования
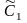 и
и
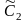 определяем при заданных начальных
условиях t=0
q(0)=q0=0,
определяем при заданных начальных
условиях t=0
q(0)=q0=0,
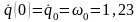 рад/с,
рад/с,
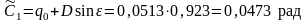 ,
,
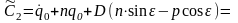
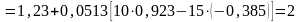 рад/с.
(15)
рад/с.
(15)
Окончательный вид решения примера:
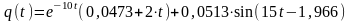 . (16)
. (16)
Вычислим
добротность системы Д и период вынужденных
колебаний
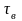 :
:
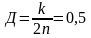 ,
,
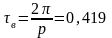 с.
(17)
с.
(17)
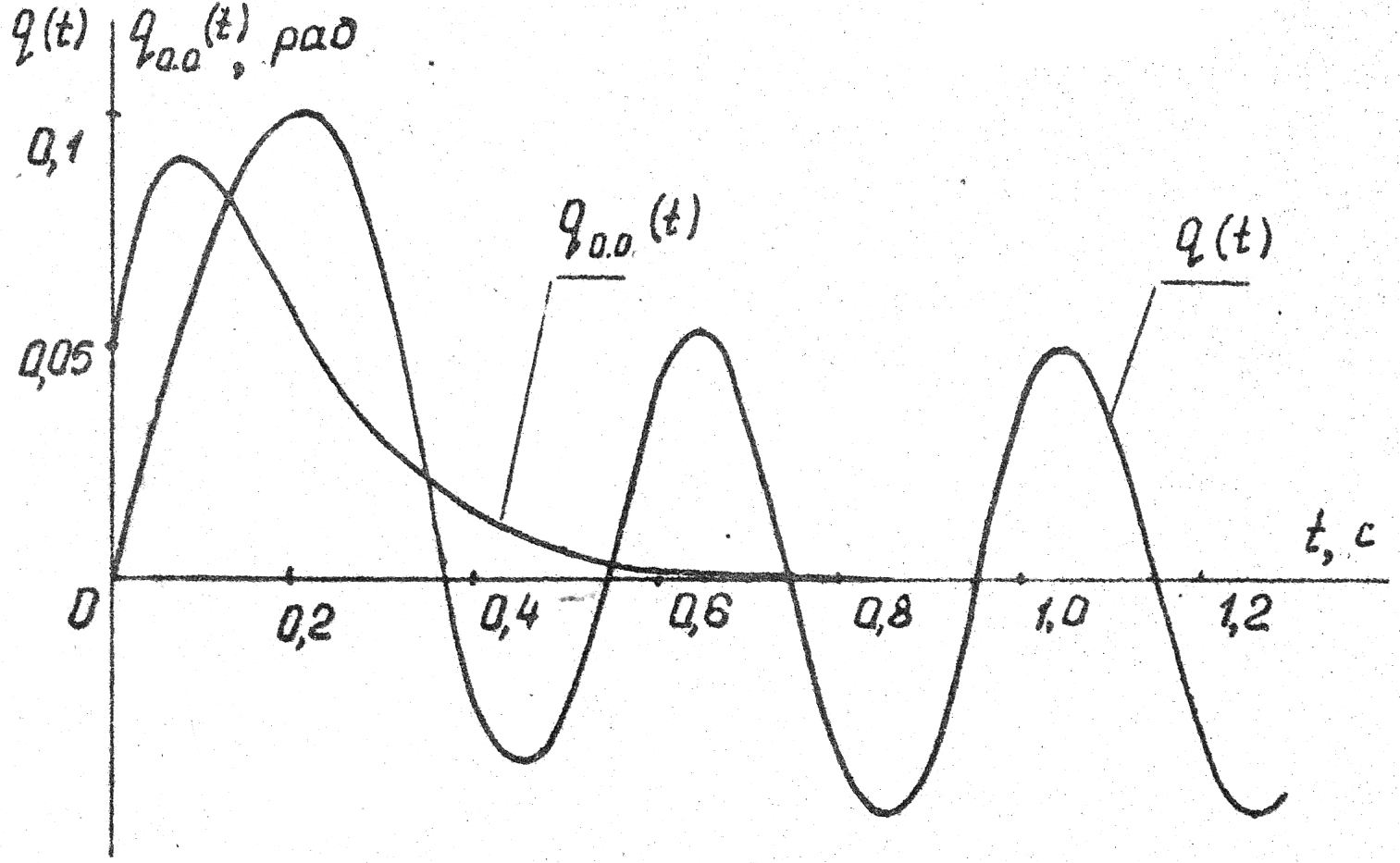
Рис.3
Для
оценки перехода от движения системы,
возникшего в начальный момент t=0
в результате начального возмущения
(q0=0,
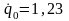 рад/с),
к установившимся вынужденным колебаниям
построим графики
рад/с),
к установившимся вынужденным колебаниям
построим графики
 и q(t)
на интервале времени
и q(t)
на интервале времени
 ,
достаточном для этого перехода:
,
достаточном для этого перехода:
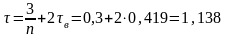 с,
с,
округлим
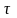 до 1,25 с.
до 1,25 с.
На
рис.3 представлены графики
и q(t).
Видно, что на выбранном интервале времени
при
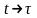
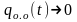 ,
а q(t)
переходит в установившиеся вынужденные
колебания.
,
а q(t)
переходит в установившиеся вынужденные
колебания.
Амплитудно-частотная
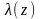 и фазочастотная
и фазочастотная
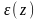 характеристики системы, построенные
по значениям, приведенным в табл.1, даны
на рис.4.
характеристики системы, построенные
по значениям, приведенным в табл.1, даны
на рис.4.
Таблица 1
z |
λ |
ε |
0 |
1 |
0 |
0,5 |
0,8 |
0,927 |
1,0 |
0,5 |
1,571 |
1,5 |
0,308 |
1,966 |
2,0 |
0,2 |
2,214 |

Рис.4
Поскольку
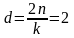 ,
максимальное значение
,
максимальное значение
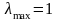 и соответствует z=0.
и соответствует z=0.
Справочно: Сдвиг по фазе ε, т.е. отставание по фазе установившихся вынужденных колебаний от вынуждающей силы
Коэффициент динамичности λ – отношение амплитуды установившихся вынужденных колебаний к статическому смещению
где
Статическое смещение системы Dст от положения равновесия под действием постоянной силы, равной амплитудному значению гармонического возмущающего воздействия
Сдвиг по фазе относительно коэффициента расстройки
Добротность
– количество полных колебаний, после
которых амплитуда уменьшится в
Если
случай
Если
Резонанс
имеет место при z=1,
и тогда
Условный период затухающих колебаний
Декремент затухания
Логарифмический декремент затухания
Постоянная времени затухающих колебаний
|
Варианты курсовой работы
Курсовая работа содержит 30 вариантов. Схемы механических систем изображены на рис.5-8. Необходимые числовые данные приведены в таблице 2 и, где это необходимо, на схемах задач. Для всех вариантов на рисунках задана обобщенная координата q(t), отсчитываемая от положения равновесия в невозмущенном состоянии, а в таблице 2 – соответствующие ей начальные условия. На всех рисунках номерами 1, 2 обозначены звенья, массу которых необходимо учитывать при составлении дифференциального уравнения движения, номером 3 – упругий элемент, номером 4 – демпфер.
Там, где это необходимо, на схемах вариантов указан радиус инерции звена относительно центральной оси, в остальных вариантах тела вращения принять за однородные сплошные цилиндры.
В
вариантах 1,2,5,16,26,28 характеристики
упругих элементов заданы через их
статические деформации
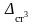 (линейные
или угловые).
(линейные
или угловые).
Внешнее воздействие во всех вариантах изменяется во времени по закону sin pt.
При выполнении курсовой работы необходимо:
Составить дифференциальное уравнение малых колебаний системы.
Получить решение этого уравнения и, используя заданные начальные условия, определить постоянные интегрирования
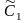 и
и
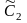 .
.Определить период установившихся вынужденных колебаний и добротность системы Д, а для вариантов с малым линейно-вязким сопротивлением (n<k) дополнительно:
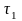 - условный период затухающих колебаний,
- условный период затухающих колебаний,
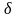 - логарифмический декремент колебаний,
- логарифмический декремент колебаний,
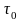 - постоянную времени затухающих
колебаний.
- постоянную времени затухающих
колебаний.Исследовать амплитудно-частотную и фазочастотную характеристики системы.
Оценить процесс перехода от начального возмущенного движения системы к установившимся вынужденным колебаниям, построив графики и
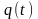 .
.

Рис.5
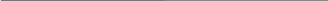
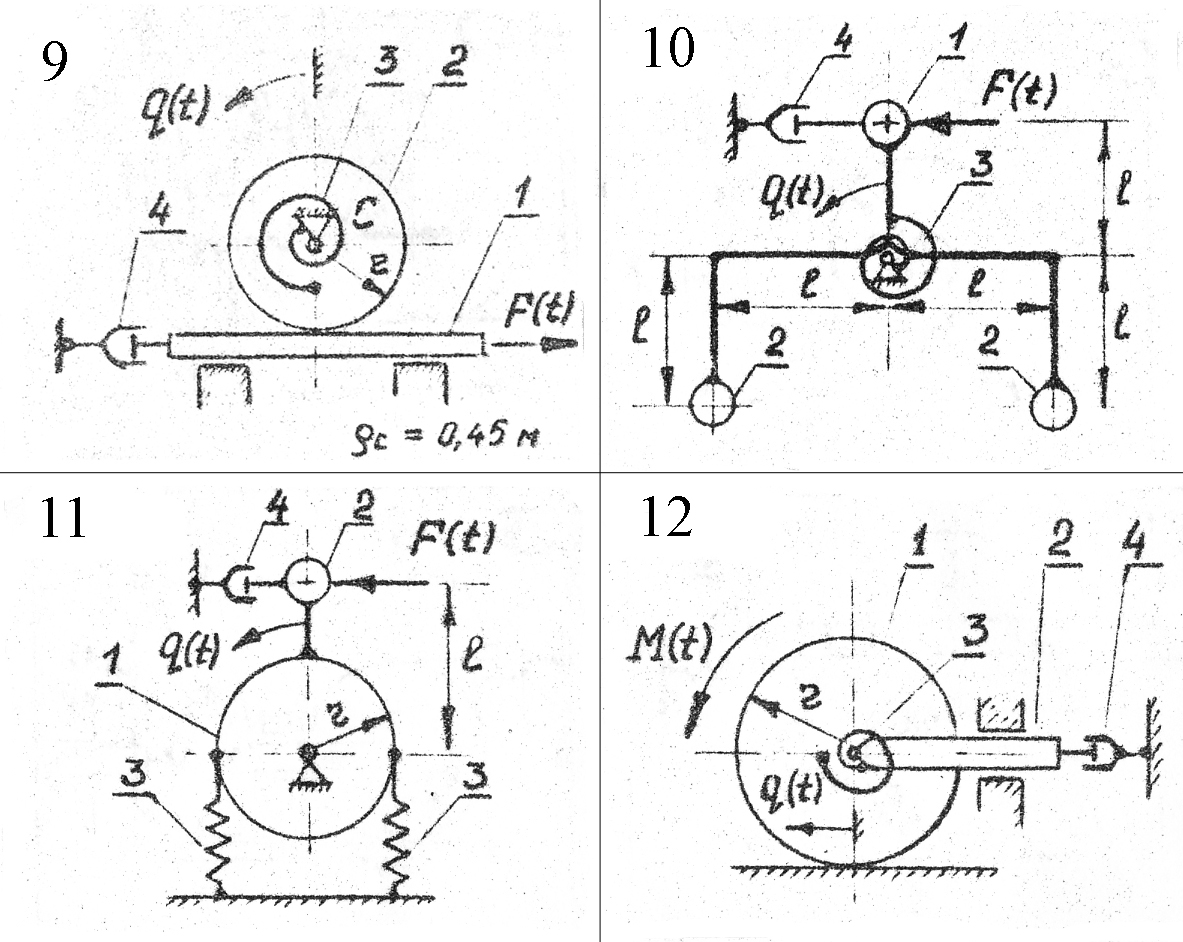
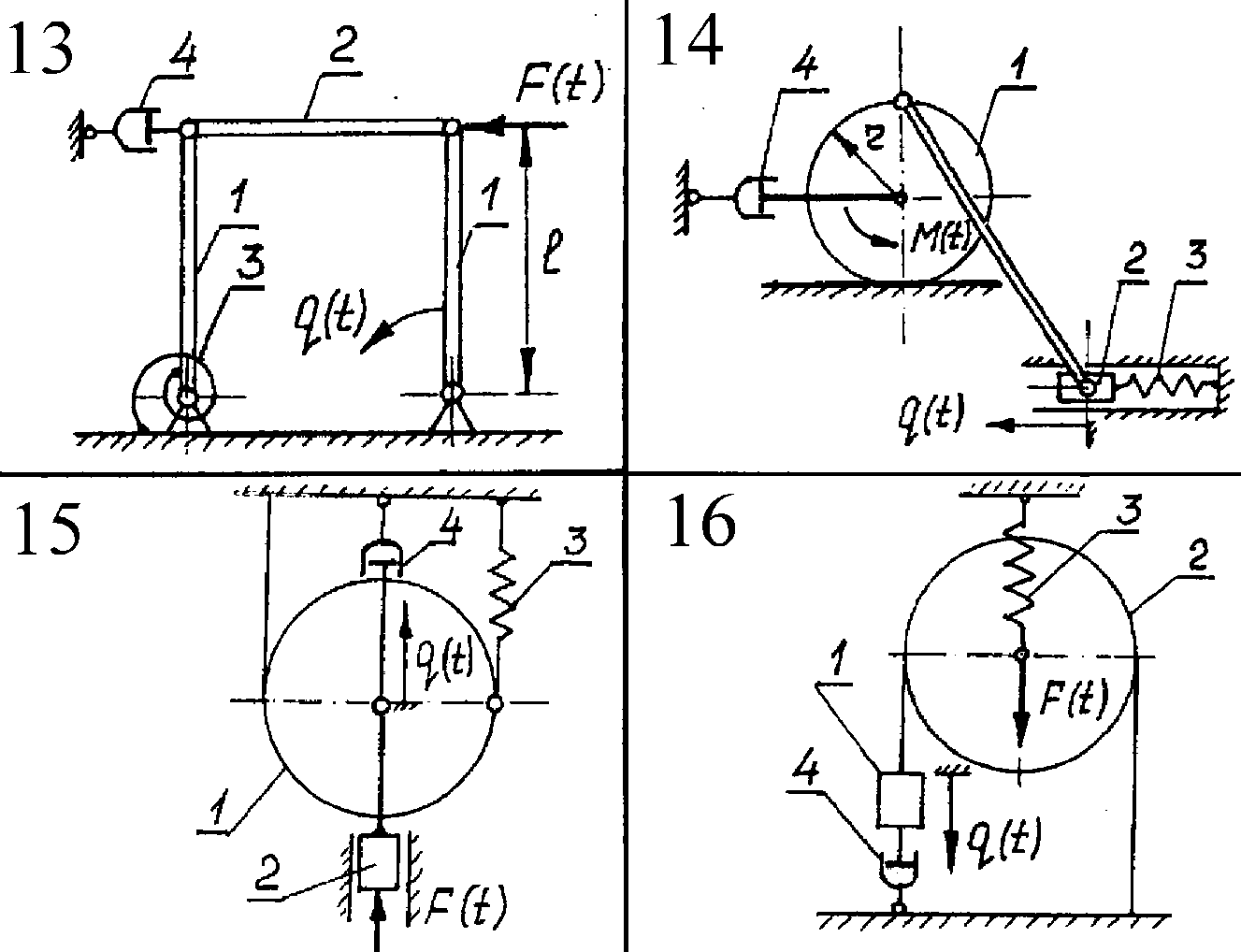
Рис.6.
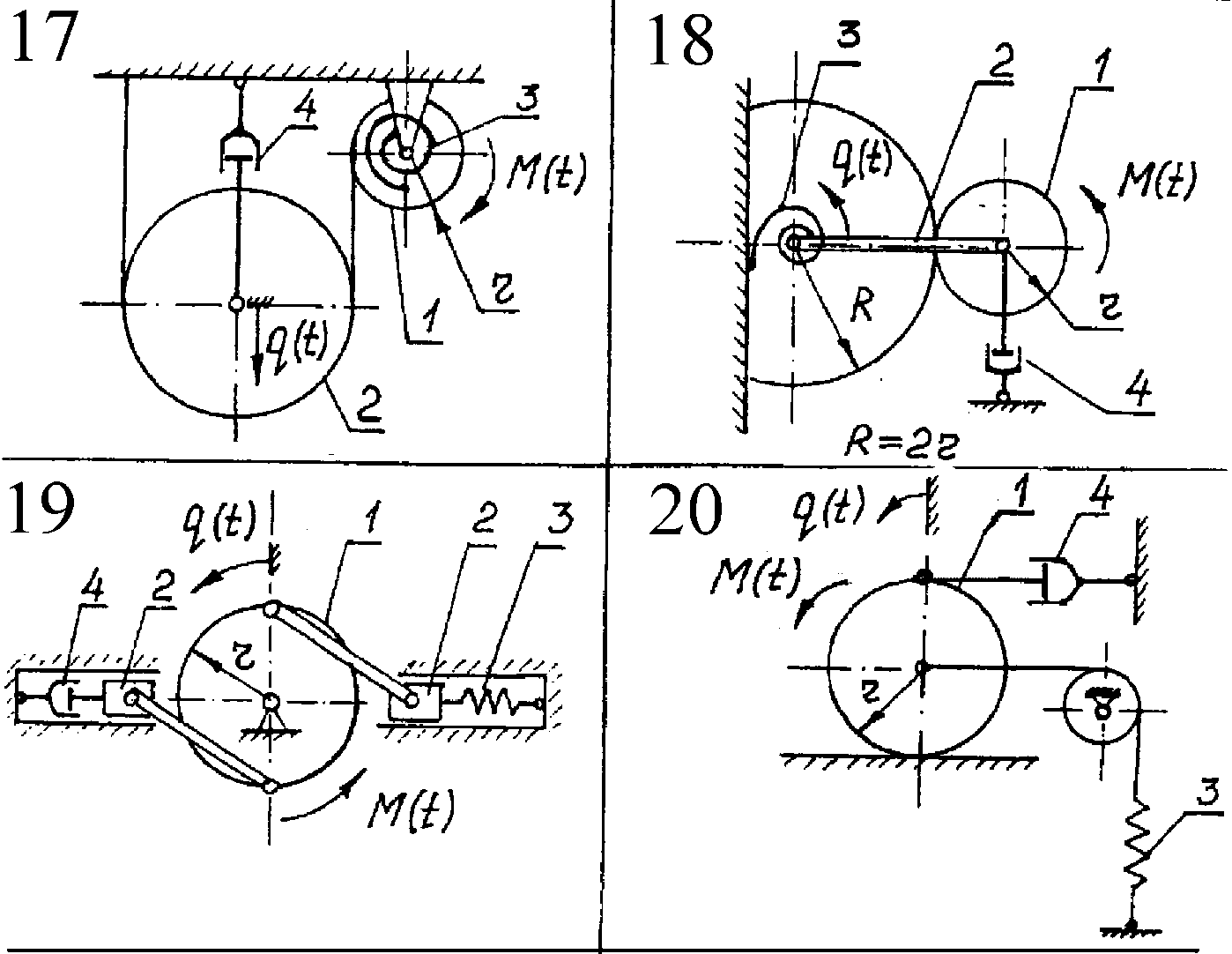
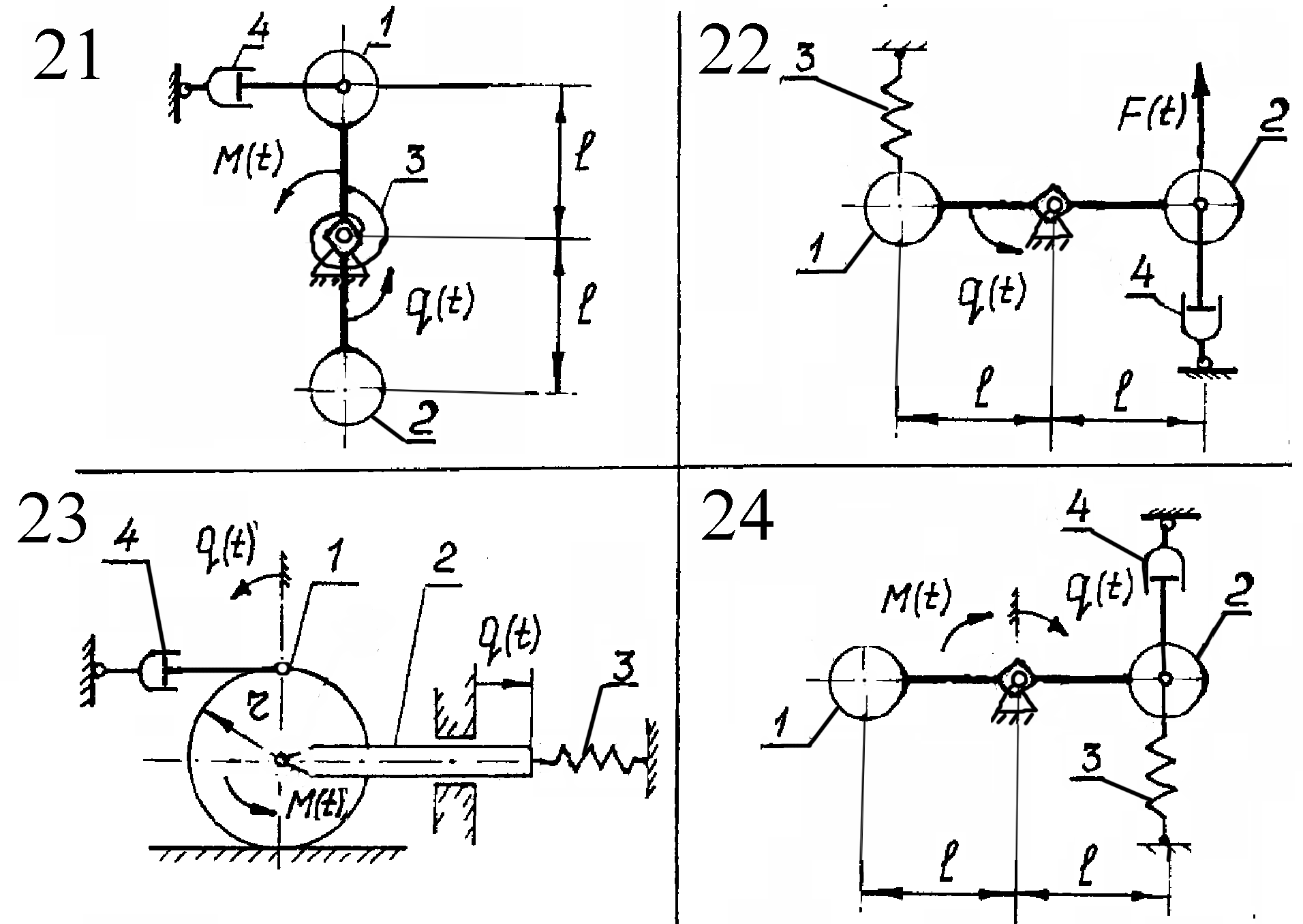
Рис.7.
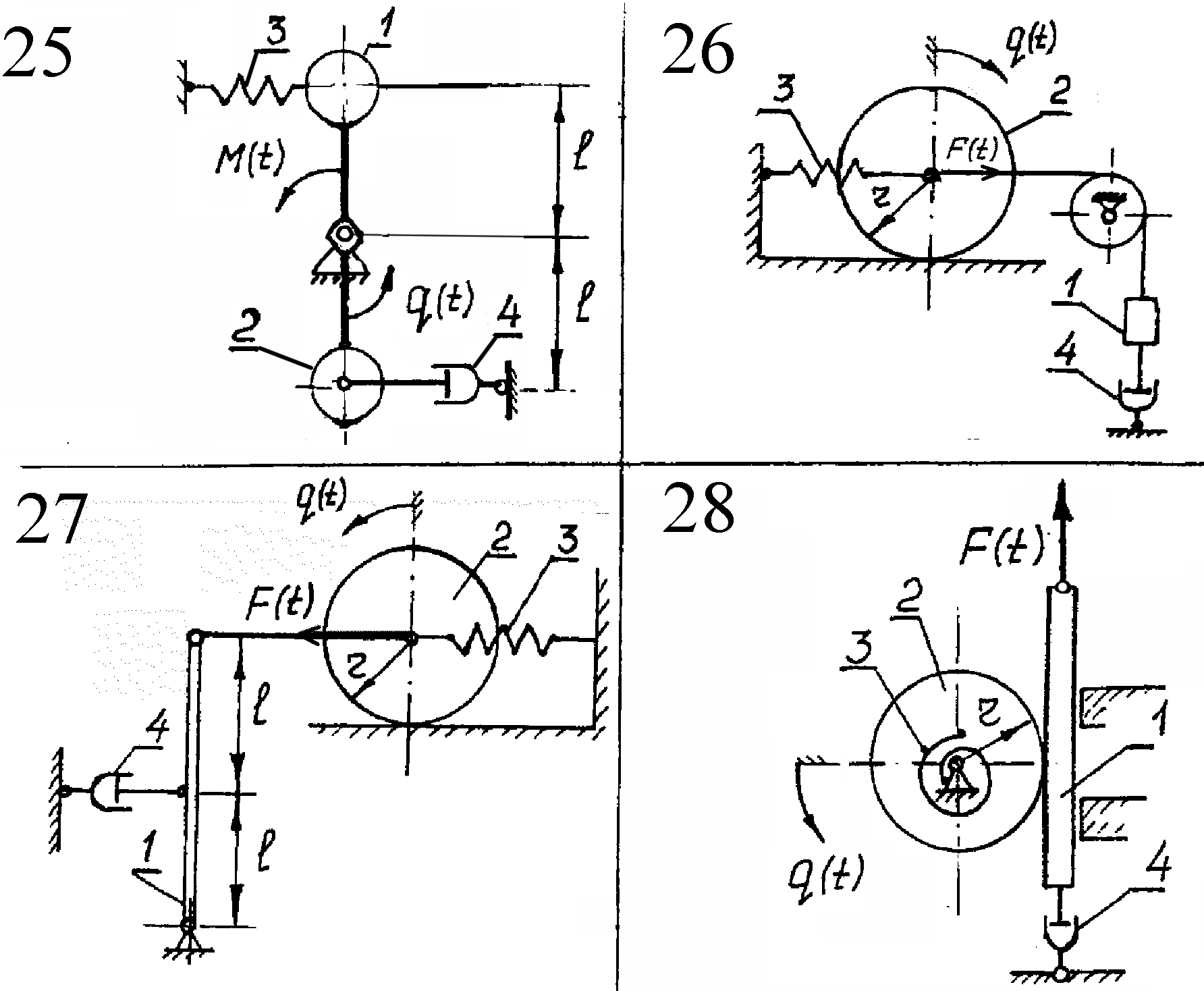
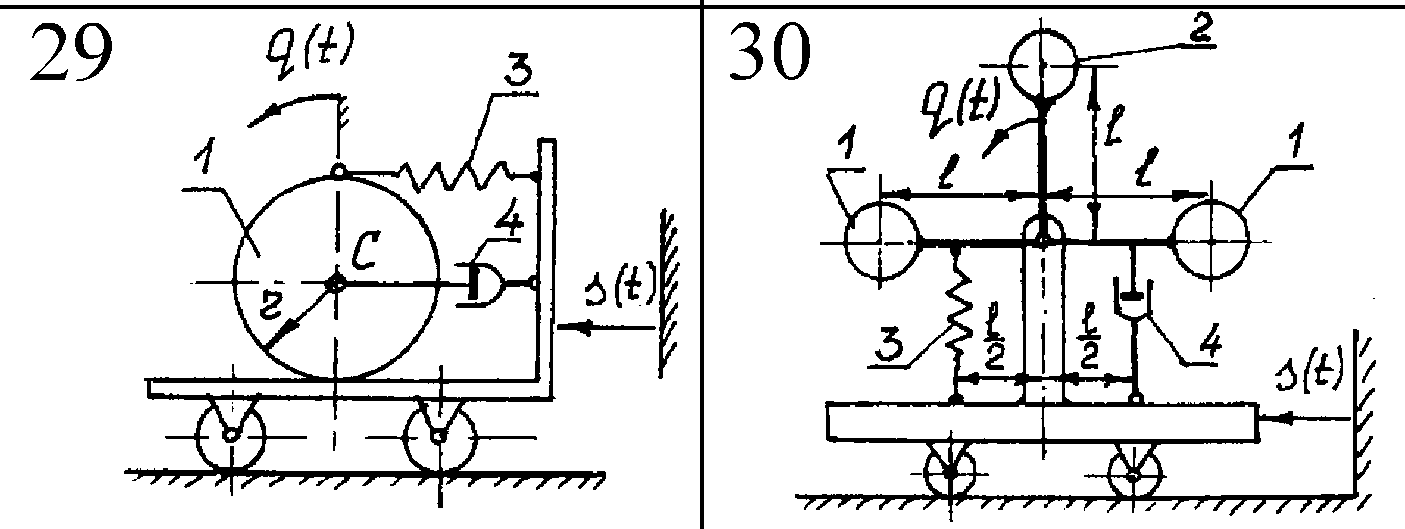
Рис.8.
Таблица 2
№ вар |
r |
l |
m1 |
m2 |
c3 |
|
|
F0(M0) |
p |
q(0) |
|
м |
м |
кг |
кг |
|
м(рад) |
|
Н( |
|
м(рад) |
|
|
1 |
0,4 |
- |
50 |
- |
- |
0,1 |
1300 |
100 |
5 |
-0,2 |
1 |
2 |
0.1 |
- |
3,8 |
4 |
- |
0,019 |
78,4 |
3 |
10 |
0,01 |
-0,1 |
3 |
0,1 |
- |
2 |
2 |
4800 |
- |
300 |
5 |
40 |
0,02 |
-0,5 |
4 |
0,2 |
0,4 |
12 |
4 |
1073,5 |
- |
480 |
10 |
9 |
0,02 |
-0,5 |
5 |
0,1 |
- |
2 |
4 |
- |
0,25 |
67,2 |
1 |
15 |
-0,02 |
-0,5 |
6 |
0,1 |
- |
5 |
- |
147 |
- |
210 |
9 |
10 |
0,06 |
-6,0 |
7 |
0,1 |
- |
8 |
6,8 |
2205 |
- |
392 |
10 |
12 |
0,1 |
1 |
8 |
0,4 |
- |
100 |
50 |
20150 |
- |
500 |
200 |
10 |
0,1 |
-1 |
9 |
0,5 |
- |
2 |
10 |
40,4 |
- |
101 |
6 |
3 |
0,02 |
0,5 |
10 |
- |
1 |
2 |
1 |
384 |
- |
120 |
36 |
8 |
0,05 |
0,5 |
11 |
0,4 |
0,8 |
4 |
2 |
549 |
- |
30 |
20 |
20 |
0,02 |
-0,5 |
12 |
0,2 |
- |
20 |
10 |
640 |
- |
320 |
100 |
20 |
0,05 |
0,2 |
13 |
- |
0,5 |
3 |
6 |
244,1 |
- |
96 |
20 |
8 |
0,1 |
1 |
14 |
0,2 |
- |
8 |
2 |
500 |
- |
400 |
12 |
11 |
0,05 |
-2,0 |
15 |
- |
- |
10 |
5 |
4500 |
- |
200 |
120 |
20 |
0,02 |
0,1 |
16 |
- |
- |
4 |
16 |
- |
0,12 |
20 |
40 |
8 |
-0,15 |
-1 |
17 |
0,2 |
- |
2 |
4 |
6,4 |
- |
40 |
1,5 |
6 |
0,1 |
-0,5 |
18 |
0,1 |
- |
6 |
3 |
360 |
- |
60 |
10 |
30 |
0,1 |
0 |
19 |
0,2 |
- |
18 |
8 |
1600 |
- |
500 |
10 |
120 |
0,05 |
-1 |
20 |
0,1 |
- |
5 |
- |
147 |
- |
200 |
9 |
10 |
0,02 |
-0,5 |
21 |
- |
1 |
2 |
2 |
400 |
- |
100 |
40 |
7 |
0,05 |
0,5 |
22 |
- |
0,5 |
1 |
1 |
200 |
- |
200 |
50 |
20 |
0,1 |
-0,5 |
23 |
0,1 |
- |
4 |
1 |
700 |
- |
21 |
100 |
10 |
0,02 |
0,5 |
24 |
- |
1 |
1 |
1 |
300 |
- |
300 |
100 |
5 |
0,05 |
-0,5 |
25 |
- |
0,5 |
2 |
2 |
450 |
- |
130 |
80 |
12 |
0,05 |
0,5 |
26 |
0,2 |
- |
12 |
13 |
- |
0,05 |
100 |
120 |
5 |
0,05 |
0,5 |
27 |
0,1 |
0,5 |
3 |
1 |
400 |
- |
300 |
20 |
10 |
0,1 |
1 |
28 |
0,2 |
- |
5 |
10 |
- |
0,2 |
50 |
2 |
10 |
0,02 |
0,5 |
29 |
0,5 |
- |
10 |
- |
6000 |
- |
150 |
- S0=0,03м |
50 |
0,1 |
-1 |
30 |
- |
0,5 |
0,5 |
1 |
3278,4 |
- |
96 |
- S0=0,05м |
16 |
0,1 |
-0,5 |

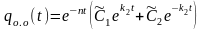 ,
,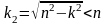 .
.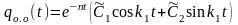 ,
,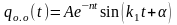 ,
,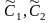 и A,
α
– произвольные постоянные, причем
и A,
α
– произвольные постоянные, причем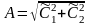 ,
,
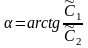 ,
,
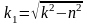 .
.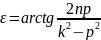
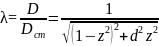
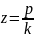 – коэффициент
расстройки,
– коэффициент
расстройки,
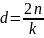 – безразмерный коэффициент сопротивления.
– безразмерный коэффициент сопротивления.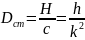
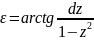
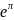 раз, т.е. колебания станут исчезающее
малыми
раз, т.е. колебания станут исчезающее
малыми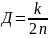
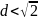 ,
то максимальное значение
,
то максимальное значение
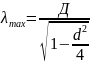 будет при
будет при
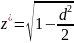 .
.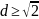 ,
то
,
то
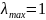 при
при
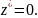
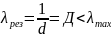 .
.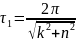
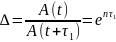
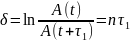
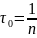
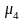
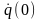
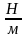
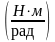
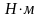 )
)