2.5. Вычисление пределов по правилу Лопиталя.

(Гильом Франсуа Антуан де Лопиталь (1661-1704), французский математик; автор первого учебника по дифференциальному исчислению).

Пусть функции и дифференцируемы в некоторой окрестности точки , за исключением, быть может, самой точки и . Пусть также (или ) в указанной окрестности точки . Тогда, если существует , то .

Правило применимо для устранения неопределенностей и других неопределенностей, к ним сводящихся.

Если в частном в точке неопределенность или по прежнему остается, то следует перейти к отношению и т. д..

Примеры. Вычислить пределы, используя правило Лопиталя.

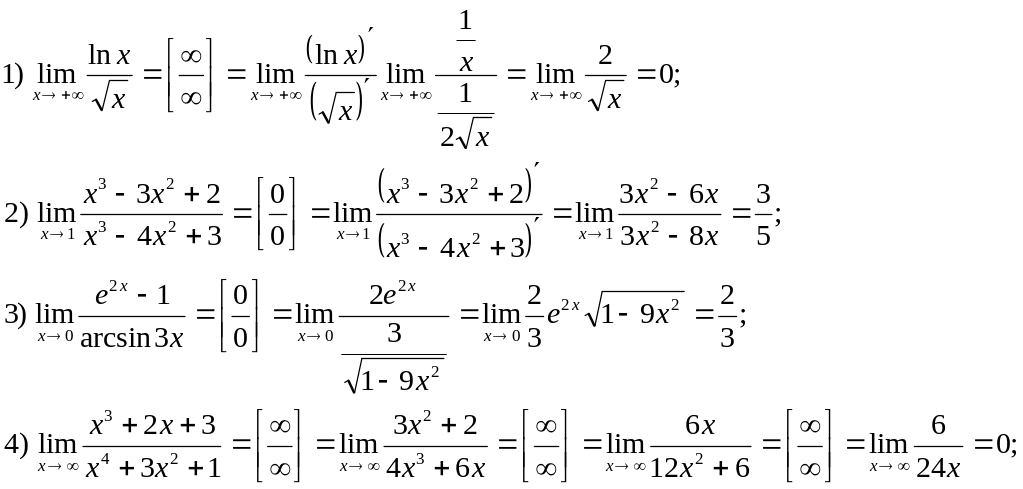
Задания для самостоятельной работы.

№1.Вычислить производные указанных функций, используя таблицу производных и правила дифференцирования:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

№2. Привести несколько примеров функции , для которой:

а)

б) ;

№3. . При каких значениях x выполняется условие:

№4. Вычислить если .

№5. Вычислить значения производной функции в точках, в которых значение этой функции равно 0:

№6. Тело движется по прямой так, что расстояние от начальной точки изменяется по закону (м), где - время движения в секундах. Через сколько секунд после начала движения тело остановится?

№7. Материальная точка массой 2г движется прямолинейно по закону ( - в сантиметрах, - в секундах). В момент времени найдите:

а) скорость движения точки;

б) ускорение движения ;

в) силу, действующую на точку .

№8. Тело, выпущенное вверх с начальной скоростью м/с, движется по закону ( - в метрах, - в секундах). Найдите момент времени, когда скорость движения тела будет в три раза меньше начальной скорости, считая что м/с.

№9. Показать, что функция обращает уравнение в тождество.

№10. Показать, что функция удовлетворяет уравнению .

№11. Показать, что функция удовлетворяет уравнению .

№12. Найти дифференциал функции в точке , если , .

№13. Найти производные второго порядка от следующих функций:

№14. Применяя правило Лопиталя вычислить пределы функций:

1. ; 2) ;

3) 4) ;

5) ; 6) ;

7) ; 8)

Ответы:

№1.1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) ; 9) ; 10) ; 11) ; 12) ; 13) ; 14) ; 15) ; 16) .

№3. а)1; -2; б) 0; -1;

№4. ;

№5. а) ; б) 2;

№6. 2 с;

№7. а) 25 см/с; б) 16 см/с ; в) 32 дины.

№8. с.

№12. ;

№13.

№14.

«Я с дрожью ужаса отворачиваюсь от ваших несчастных

проклятых функций, у которых нет производных».

(Ш. Эрмит)

§3. Исследование функций при помощи производных.

Возможность применения производных для исследования функций основана на зависимости, существующей между производными и особенностями графика функции.