2.3. Производные высших порядков.

Производную функции называют также производной первого порядка. Функция также может быть дифференцируемой, ее производная будет называться производной второго порядка функции .

Обозначение: , .

Производная от производной второго порядка (если она существует) называется производной третьего порядка и т. д.

Производной - го порядка называется производная от производной - го порядка, т. е. .

Для обозначения производных четвертого и выше порядков используют римские цифры. Например, или - производная шестого порядка. Производные порядков, выше первого, называются производными высших порядков.

Пример 1. Вычислить производную третьего порядка функции .

Решение: Нахождение производной третьего порядка необходимо начать с производной первого порядка.

.

Если функция описывает закон прямолинейного движения материальной точки, то производная второго порядка функции представляет собой скорость изменения скорости функции (т. е. ускорение) в определенный момент времени . В этом состоит ее физический смысл.

Пример 2. Найти зависимость ускорения прямолинейного движения, заданного законом от времени .

Решение:

.

Пример 3. Точка движется прямолинейно по закону

Найти скорость и ускорение движения точки для момента времени t=1 (S дается в сантиметрах ,t -в секундах ).

Решение: скорость ;

ускорение Следовательно, в момент времени t = 1:

2.4. Дифференциал функции. Геометрический смысл дифференциала.

С понятиями производной тесно связано понятие дифференциала (от него происходит название дифференциального исчисления). Пусть функция определена в некоторой окрестности точки . Дадим аргументу приращение и рассмотрим приращение функции .

Определение. Функция называется дифференцируемой в точке , если приращение функции в точке может быть представлено в виде , где и - бесконечно малые при , причем - бесконечно малая величина одного порядка с ( - бесконечно малая функция более высокого порядка, чем ). Величина называется главной частью приращения функции или дифференциалом функции в точке и обозначаемая .

Определение. Дифференциалом функции в точке называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, т. е. ил .

Примеры.

1). Найти дифференциал функции .

Решение.По формуле находим .

2).Найти дифференциал функции в точке , если .

Решение: .

.

Геометрический смысл дифференциала:

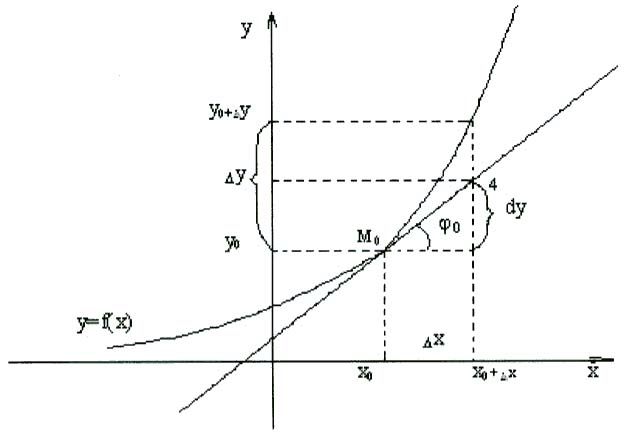
L

K

Рис. 8

Проведем к графику функции в точке касательную , угол наклона которой равен . Рассмотрим , в котором сторона . Учитывая, что , , получим: , сравнивая с определением дифференциала функции.

.

Т.о. дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в этой точке, когда аргумент получит приращение (рис.8). Из определения дифференциала и правил вычисления производных следуют правила вычисления дифференциала функции:

1. ;

2. ;

3. ;

4. ;