
Исследуем форму распределения.
Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.
Симметричным считается распределение, в котором частоты двух равностоящих от центра значений признака равны между собой.
Степень асимметрии распределения в центральной его части определяется с помощью коэффициента асимметрии Пирсона.
![]()
Степень асимметрии
![]() следовательно наблюдается правосторонняя
симметрия.
следовательно наблюдается правосторонняя
симметрия.
Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка.
Расчетная
таблица для определения ![]() и
и ![]() .
.
№ гр |
середина интервала bi |
частота ni |
xi–
|
Расчет μ3 |
Расчет μ4 |
||
(xi– )3
|
(xi– )3 * ni
|
(xi– )4
|
(xi– )4* ni |
||||
1. |
450 |
24 |
-570 |
-185193000 |
-4444632000 |
105560010000 |
2533440240000 |
2. |
950 |
9 |
-70 |
-343000 |
-3087000 |
24010000 |
216090000 |
3. |
1450 |
9 |
430 |
7950700 |
71556300 |
34188010000 |
307692090000 |
4. |
1950 |
5 |
930 |
804357000 |
4021785000 |
748052010000 |
3740260050000 |
5. |
2450 |
1 |
1430 |
2924207000 |
2924207000 |
4181616010000 |
4181616010000 |
6. |
2950 |
1 |
1930 |
7189057000 |
7189057000 |
13874880010000 |
13874880010000 |
7. |
3450 |
1 |
2430 |
14348907000 |
14348907000 |
34867844010000 |
34867844010000 |
∑ |
13650 |
50 |
6510 |
25088942700 |
24107793300 |
53812164070000 |
2690608203500000 |
Асимметрия в крайних частях распределения определяется через коэффициент асимметрии, рассчитанный на основе центрального момента третьего порядка.
![]() ,
где
,
где ![]() – центральный момент третьего порядка,
а
– центральный момент третьего порядка,
а ![]() – среднее квадратичное отклонение в
третьей степени.
– среднее квадратичное отклонение в
третьей степени.

На
основании вычислений можно сделать
вывод, что ![]() ,
а значит, в целом по всему ряду наблюдается
правосторонняя умеренная асимметрия.
,
а значит, в целом по всему ряду наблюдается
правосторонняя умеренная асимметрия.
Для одновершинных
распределений рассчитывается еще один
показатель оценки его формы – эксцесс.
Эксцесс является показателем
островершинности распределения. Он
рассчитывается для симметричных
распределений на основе центрального
момента 4-ого порядка ![]() :
:
![]() ,
где
- центральный момент четвертого порядка,
а
,
где
- центральный момент четвертого порядка,
а ![]() -
среднее квадратичное отклонение в
четвертой степени.
-
среднее квадратичное отклонение в
четвертой степени.

По вычисленному эксцессу можно сделать вывод, что Ex>0, а значит, распределение относится к островершинным.
Теоретическое построение ряда.
Эмпирические кривые распределения, построенные на основе, как правило, небольшого числа наблюдений очень трудно описать аналитически, поэтому для выявления статистических закономерностей, сравнения и обобщения различных совокупностей аналогичных данных используются теоретические распределения.
Теоретические распределения – это хорошо изученные в теории распределения, представляющие собой зависимости между плотностями распределения и значениями признака, отражающие закономерности распределения.
Исследование формы
распределения предполагает замену
эмпирического распределения известным
теоретическим, близким ему по форме.
При этом необходимо соблюдать условие:
различия между эмпирическим и теоретическим
распределениями должны быть минимальными.
Это означает, что сумма частот эмпирического
распределения должна соответствовать
сумме частот теоретического распределения,
т.е., ![]() где
где ![]() -
частота теоретического распределения.
Теоретическое распределение в этом
случае является некоторой идеализированной
моделью эмпирического распределения,
и анализ вариационного ряда сводится
к сопоставлению эмпирического и
теоретического распределений и
определению различий между ними.
-
частота теоретического распределения.
Теоретическое распределение в этом
случае является некоторой идеализированной
моделью эмпирического распределения,
и анализ вариационного ряда сводится
к сопоставлению эмпирического и
теоретического распределений и
определению различий между ними.
Функция нормального распределения выглядит следующим образом:
![]() ,
где
,
где ![]() - относительная плотность распределения
(ордината кривой нормального распределения);
- относительная плотность распределения
(ордината кривой нормального распределения);
![]() ,
,
![]() - математические константы;
- математические константы;
- среднее значение признака в распределении;
![]() - среднее квадратичное отклонение.
- среднее квадратичное отклонение.
Пользоваться функцией
нормального распределения в её
первоначальном виде сложно, так как для
каждой пары значений
![]() и σ необходимо создавать свои таблицы
значений. Поэтому функцию стандартизируют
и затем используют для обработки рядов
распределения, для чего вводится понятие
стандартного отклонения
и σ необходимо создавать свои таблицы
значений. Поэтому функцию стандартизируют
и затем используют для обработки рядов
распределения, для чего вводится понятие
стандартного отклонения ![]() :
:
![]() тогда:
тогда:![]() .
.
Выражение ![]() .
состоит из констант, не содержит
параметров, называется стандартизованной
функцией нормального распределения.
Для неё разработаны специальные таблицы,
позволяющие находить конкретные значения
.
состоит из констант, не содержит
параметров, называется стандартизованной
функцией нормального распределения.
Для неё разработаны специальные таблицы,
позволяющие находить конкретные значения
![]() при различных значениях аргумента
(таблица значений функции Лапласа).
при различных значениях аргумента
(таблица значений функции Лапласа).
Исходная функция нормального распределения связана со стандартизированным соотношением:
![]() .
.
Для получения частот
теоретического распределения
необходимо иметь в виду, как относительная
плотность распределения
связана с одной стороны с частотой ![]() ,
а с другой - со стандартизованной функцией
нормального распределения
.
Эти связи выражаются следующими
зависимостями:
,
а с другой - со стандартизованной функцией
нормального распределения
.
Эти связи выражаются следующими
зависимостями:
![]() .
.
С другой стороны, , таким образом, имеет место равенство:
![]() ,
отсюда
,
отсюда ![]() ;
где
;
где ![]() - ширина интервала,
- ширина интервала,
![]() – объем статистической совокупности,
– объем статистической совокупности,
- среднее квадратическое отклонение,
- стандартизованная функция нормального распределения.
№ гр. |
Середина интервала
|
Частота
|
|
|
|
|
|
|
|
1 |
450 |
24 |
-570 |
-0,79 |
0,292 |
11 |
13 |
169 |
15,36 |
2 |
950 |
9 |
-70 |
-0,09 |
0,3973 |
14 |
-5 |
25 |
1,78 |
3 |
1450 |
9 |
430 |
0,6 |
0,3332 |
12 |
-3 |
9 |
0,75 |
4 |
1950 |
5 |
930 |
1,3 |
0,1714 |
6 |
-1 |
1 |
0,16 |
5 |
2450 |
1 |
1430 |
2 |
0,054 |
2 |
-1 |
1 |
0,5 |
6 |
2950 |
1 |
1930 |
2,7 |
0,0104 |
1 |
0 |
0 |
0 |
7 |
3450 |
1 |
2430 |
3,4 |
0,0026 |
0 |
-1 |
1 |
0 |
Σ |
|
50 |
|
|
|
45 |
|
|
18,55 |
Для определения близости эмпирического и теоретического распределений, можно построить эмпирическую и теоретическую кривые распределения. Их сопоставление позволяет оценить степень расхождения между ними.
Эмпирическую кривую
строим по точкам с координатами {
,
},
теоретическую – по точкам с координатами
{
,![]() }.
}.
Теоретическая кривая
Для получения объективной оценки расхождения между эмпирической и теоретической кривыми распределения используются специальные статистические показатели – критерии согласия.
Наиболее часто на практике используются следующие критерия согласия:
«хи-квадрат»- критерий (критерий Пирсона);
«лямбда»- критерий» (критерий Колмогорова).
«Хи-квадрат». Его величина определяется по формуле:
![]()
![]() 18,5
18,5
Тогда расчётное
значение ![]() выбираем по
таблице при а=0,3 (уровень значимости) и
выбираем по
таблице при а=0,3 (уровень значимости) и
![]() (число
степеней свободы данного распределения).
(число
степеней свободы данного распределения).
![]() 18,5
18,5
![]() значит,
считается, что распределения отдалены
друг от друга, различия между ними
существенны.
значит,
считается, что распределения отдалены
друг от друга, различия между ними
существенны.
Вывод:
Целью данной работы является построение и исследование вариационного ряда. Для этого нам нужно было выполнить два этапа - эмпирическое и теоретическое исследование.
На первом этапе мы по исходным данным построили вариационный ряд, рассчитали частотные характеристики: частоту, частость, накопленную частоту, накопленную частость и графически представили вариационный ряд в виде гистограммы.
При исследовании вариационного ряда последовательно решали следующие задачи:
Определяли положение центра распределения с помощью таких показателей, как: среднее значение признака (
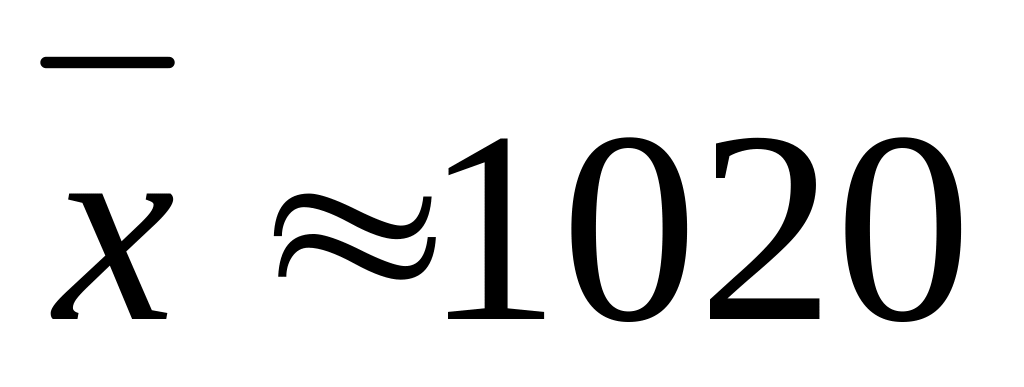 км),
мода (Мо=410
км), медиана (Ме=478 км) - является типичным
значением совокупности, так как она
нечувствительна к крайним значениям
признака.
км),
мода (Мо=410
км), медиана (Ме=478 км) - является типичным
значением совокупности, так как она
нечувствительна к крайним значениям
признака.
Оценивали степень однородности распределения, используя показатели вариации: размах вариации (R=3300), дисперсия, среднеквадратичное отклонение, коэффициент вариации (V=70%). Коэффициент вариации используется для характеристики однородности исследуемой совокупности. Исследуемый ряд распределения считается неоднородным, т.к. коэффициент вариации превышает 33% и колеблемость признака – высокая.
Исследовали форму распределения, оценивая степень асимметрии
 и эксцесс
и эксцесс  распределения. На основании расчёта
коэффициента асимметрии Пирсона
(As=0,85-
асимметрия в центральной части) и
коэффициента асимметрии по краям
(As=1,32)
можно сделать вывод, что наблюдается
правосторонняя умеренная асимметрия
(если |As|>0,5
то асимметрия считается значительной).
По вычисленному эксцессу (Ex=10337,6)
можно сделать вывод, что Ex>0,
а значит, распределение относится к
островершинным.
распределения. На основании расчёта
коэффициента асимметрии Пирсона
(As=0,85-
асимметрия в центральной части) и
коэффициента асимметрии по краям
(As=1,32)
можно сделать вывод, что наблюдается
правосторонняя умеренная асимметрия
(если |As|>0,5
то асимметрия считается значительной).
По вычисленному эксцессу (Ex=10337,6)
можно сделать вывод, что Ex>0,
а значит, распределение относится к
островершинным.
Второй этап - теоретическое исследование, в котором анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений и определению различий между ними. Для построения теоретического распределения воспользовались функцией нормального распределения: ,.
Рассчитали стандартное отклонение , и теоретическую частоту. После сравнения суммы эмпирических частот с суммой теоретических частот, пришли к выводу, что теоретический аналог подобран верно. Наглядно это видно на графике кривых распределения.
Для получения
объективной оценки расхождения между
кривыми используют критерии согласия.
В нашем случае условие
выполняется, значит, считается, что
распределения отдалены друг от друга,
различия между ними существенны. (![]() 18,5
, 18,5
).
18,5
, 18,5
).
