Санкт-петербургский государственный университет информационных технологий механики и оптики

Гуманитарный факультет

Кафедра прикладной информатики

в экономике

Практическая работа №1

«Построение и исследование вариационного ряда»

по дисциплине статистика

Выполнил: Луговая Карина и Гуменюк Алина

группа 2070

преподаватель: Сизова Т.М.

Ряд распределения рейса по расстоянию перевозок (км).

Цель работы: построение и исследование вариационного ряда.

1. Построение вариационного ряда и расчет его частотных характеристик

№ гр.	Наименование признака, единицы измерения				Частотные характеристики
	границы		ширина интервала аi	середина интервала bi	частота ni	частость qi	накопленная частота Ni*	накопленная частость Qi*
	xiн	xiв
1.	200	700	500	450	24	0,48	24	0,48
2.	700	1200		950	9	0,18	33	0,66
3.	1200	1700		1450	9	0,18	42	0,84
4.	1700	2200		1950	5	0,1	47	0,94
5.	2200	2700		2450	1	0,02	48	0,96
6.	2700	3200		2950	1	0,02	49	0,98
7.	3200	3700		3450	1	0,02	50	1
всего	200	3700	500

2. Графическое представление вариационного ряда

• В виде гистограммы распределения:

• В виде кумулятивного распределения

Исследование вариационного ряда.

Расчетная таблица для определения и σ²

№ гр	Наименование признака, единицы измерения				Частота ni	Расчет x			Расчет σ2
	Границы групп			середина интервала bi		bi*ni			bi2	bi2*ni
	xiн	xiв
1.	200	700		450	24	10800			202500	4860000
2.	700	1200		950	9	8550			902500	8122500
3.	1200	1700		1450	9	13050			2102500	18922500
4.	1700	2200		1950	5	9750			3802500	19012500
5.	2200	2700		2450	1	2450			6002500	6002500
6.	2700	3200		2950	1	2950			8702500	8702500
7.	3200	3700		3450	1	3450			11902500	11902500
∑					50					77525000

Определим положение центра распределения через среднее значение, моду, медиану.

1. Среднее значение признака определяется по формуле:

, где - середина соответствующего интервала.

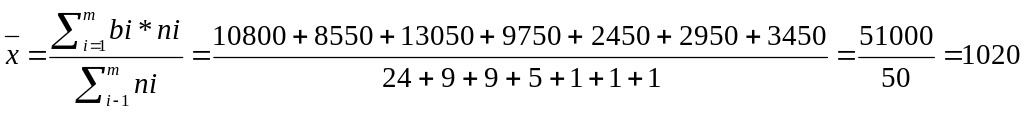
2. Мода – наиболее часто встречаемое значение признака.

Мода в интервальных вариационных рядах определяется следующим образом:

- по максимальному значению частоты – интервал, носящий моду (5-6)

- в рамках модального интервала мода вычисляется по формуле:

3. Медиана – значение признака у статистической единицы, находящейся в центре

распределения. В интервальных вариационных рядах определяется следующим образом:

- по накопленным частотам определяется медианный интервал – интервал,

содержащий статистическую единицу, носящую медиану (5-6)

- в пределах медианного интервала вычисляется по формуле:

Рассчитываем показатели, характеризующие вариацию признака для оценки степени однородности ряда.

К абсолютным показателям вариации относятся:

- размах вариации ,

- средний квадрат отклонений (дисперсия) ,

- среднее квадратическое отклонение ,

1. Размах вариации характеризует разброс элементов совокупности, улавливает только

крайние значения признака в совокупности, не учитывает повторяемость его промежуточных

значений, а также не отражает отклонений всех вариантов значений признака.

R=x_max-x_min=3500-200=3300

2. Дисперсия признака представляет собой средний квадрат отклонений вариантов

от их средней величины, является общепринятой мерой вариации.

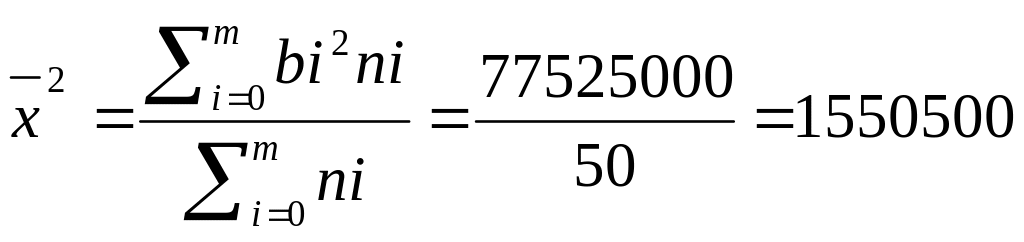
3. Среднее квадратичное отклонение.

Коэффициент вариации.

Коэффициент вариации используется для характеристики однородности исследуемой совокупности. В данном случае ряд распределения считается неоднородным, т.к. коэффициент вариации превышает 33% и колеблемость признака – высокая.