20

Министерство образования и науки Украины

Севастопольский национальный технический университет

Кафедра кибернетики и вычислительной техники

Курсовая работа

по дисциплине «Математической моделирование и вычислительная техника»

на тему: «Оценка характеристик открытой экспоненциальной сети»

Вариант №7

Выполнил: студент группы МАГ-3

Васильев А.В.

Проверил: Кирюхин В.В.

Севастополь

2007

Содержание

Постановка задания	3
1. Описание математической модели	4
1.1. Стохастические сети массового обслуживания	4
1.2. Характеристики разомкнутых СтМО	8
2. Расчет характеристик сети	11
Выводы	21
Перечень ссылок	22

Постановка задания

открытая экспоненциальная стохастическая сеть массового обслуживания задана в виде графа из 9 узлов. Узел является источником заявок и характеризуется интенсивностью потока заявок. Остальные узлы являются системами массового обслуживания (СМО) и характеризуется каждый двумя параметрами: средним временем обслуживания заявки и числом обслуживающих каналов. Каждая СМО является системой типа . Связь между СМО сети отображается на графе в виде дуги между узлами и с весом — вероятностью передачи заявки из в .

Требуется:

1. Изобразить сеть в виде графа.

2. Вычислить интенсивность источника, при которой в сети еще возможен стационарный режим обслуживания заявок.

3. Полагая , определить узловые и сетевые характеристики, а именно: среднюю длину очереди, среднее время пребывания заявки в очереди (в очередях), среднее число заявок в узле (в сети), среднее время пребывания заявок в узле (в сети) — для всех СМО и для сети в целом.

1. Описание математической модели

1.1. Стохастические сети массового обслуживания

Сетью массового обслуживания (СтМО) называется совокупность СМО, обменивающихся между собой заявками. Если этот обмен носит случайный характер и заявки обслуживаются по случайным законам, то сеть называется стохастической. СтМО можно изображать в виде графа с узлов, где 0 — источник заявок, а остальные узлов — система МО ( ).

В такой сети — интенсивность потока заявок. характеризуется следующими величинами: , где — количество каналов в СМО; — время обслуживания в i СМО.

Каждая сеть характеризуется матрицей вероятностных переходов , где — вероятность того, что заявка из -ой СМО перейдет в -ую СМО. Все вероятности соответствуют условию

,

но .

Из этого вытекает следующее свойство стохастической сети:

;

.

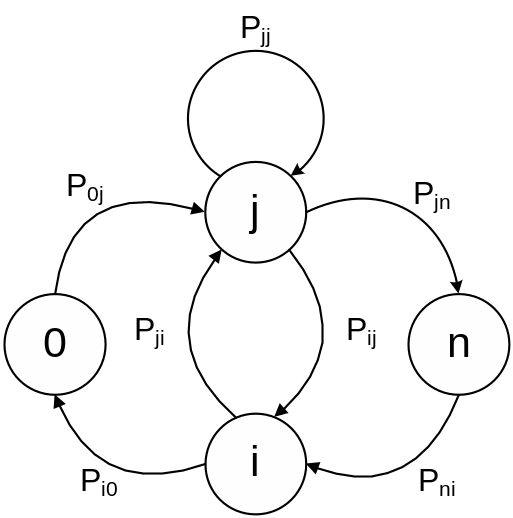
Стохастическая сеть массового обслуживания [4] изображена на рисунке 1.

— вероятность окончания обслуживания; — вероятность попадания

из источника в СМО.

Рис. 1 — Стохастическая сеть массового обслуживания

Если в сети существует стационарный режим, то имеет место следующее равенство

.

Рассмотрим сеть в стационарном режиме (рисунок 2).

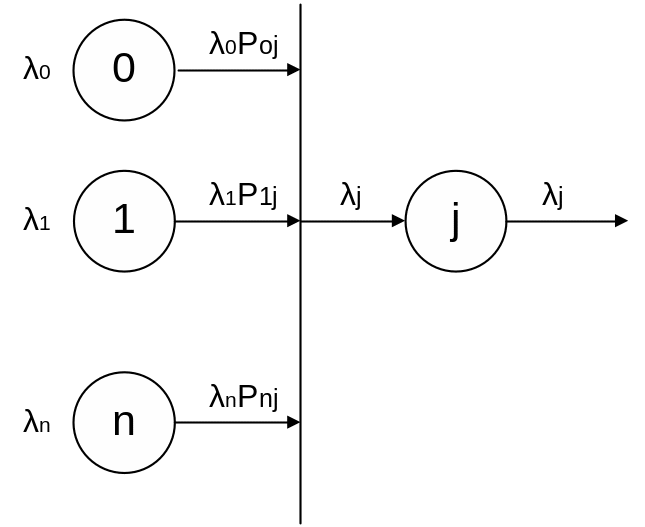
Рис. 2 — Сеть в стационарном режиме

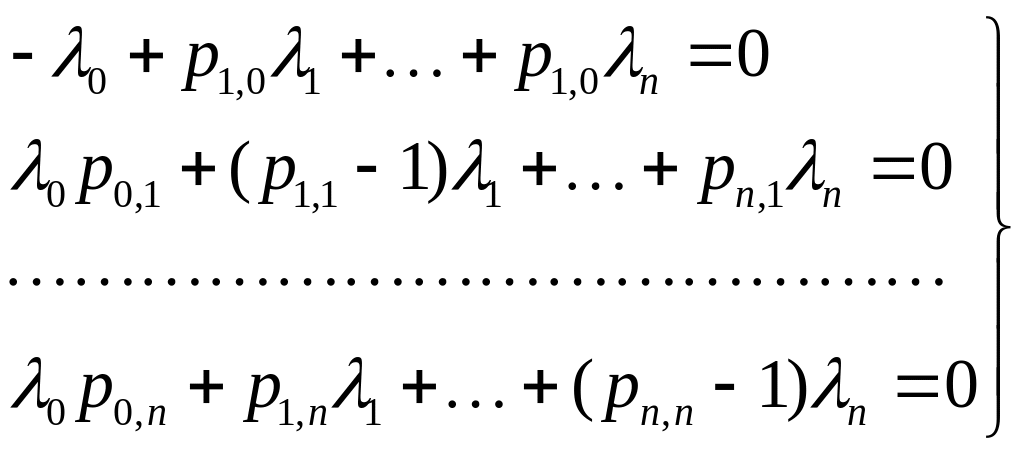
Составим определитель, для нахождения решений данной системы

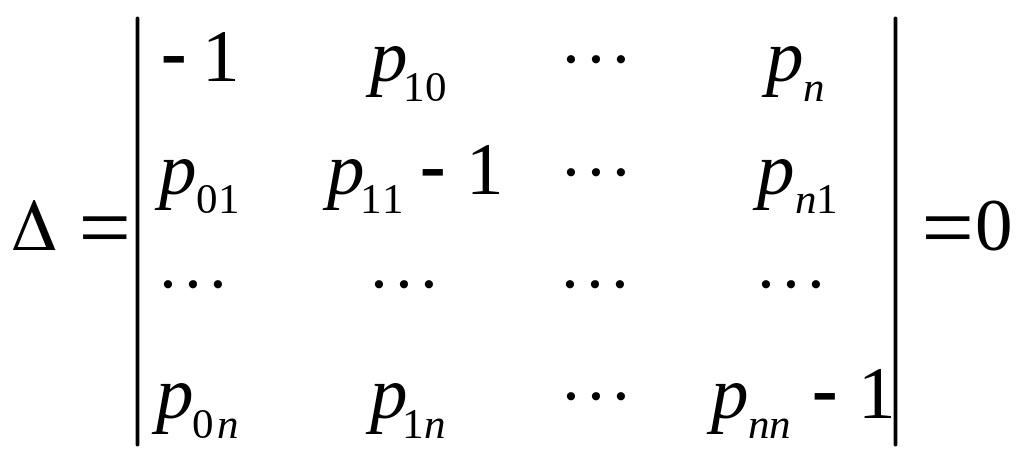
Так как определитель равен нулю, то система имеет бесконечное количество решений.

где — среднее число пребываний заявки в узле , до того, как она покинет сеть.

Основная задача при рассмотрении стохастической СтМО заключается в нахождении узловых и сетевых характеристик в стационарном режиме.

Узловые характеристики представлены: Надо определять характеристик.

Сетевые характеристики представлены:

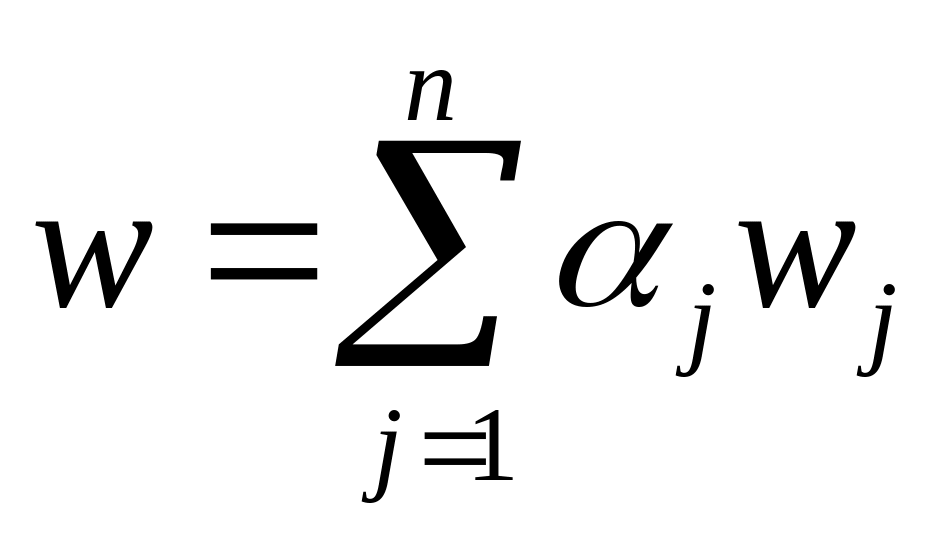• — суммарное время ожидания заявки в очередях сети;

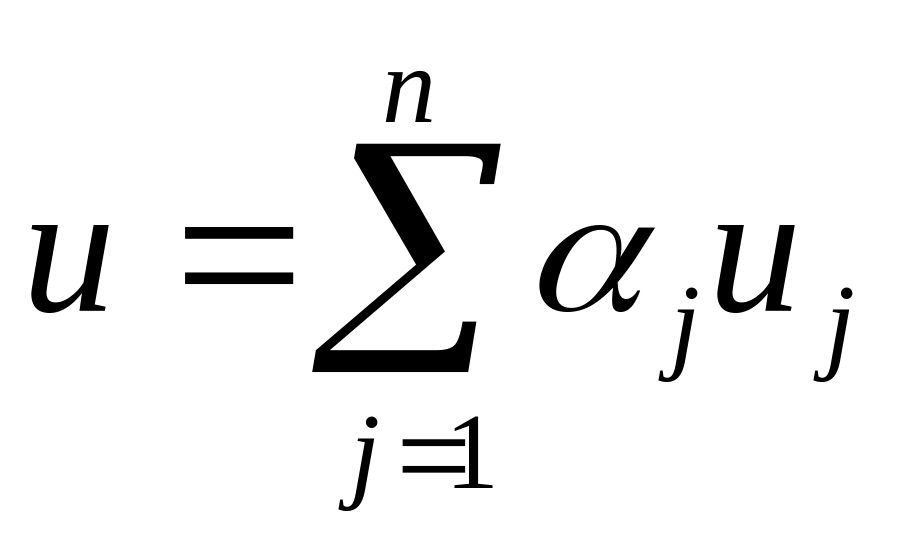• — суммарное среднее время пребывания заявки в сети;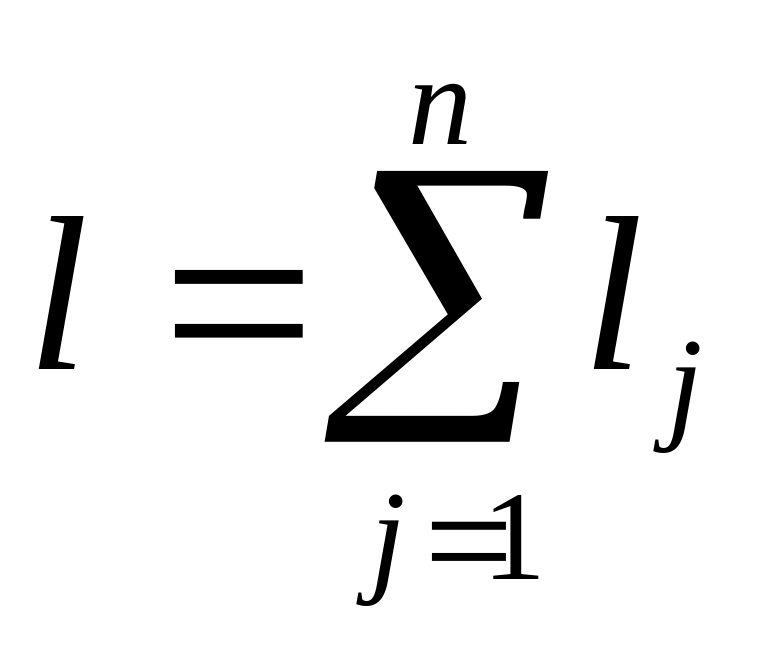

• — среднее количество заявок, находящихся в очередях сети;

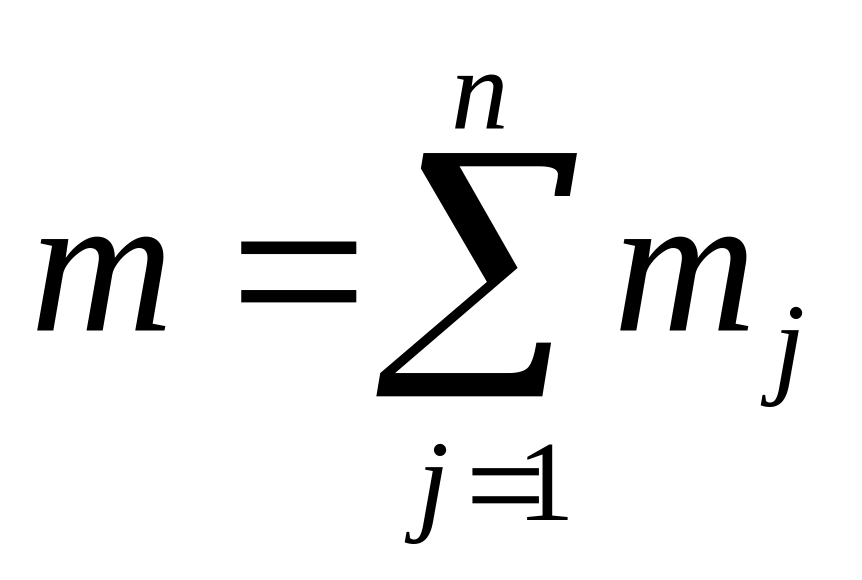• — среднее количество заявок, пребывающих в сети.

Если сеть находится в стационарном режиме и в ней нет потерь, то для каждого узла имеем:

;

;

,

следовательно получим:

;

.

Последние выражения представляют собой сетевые формулы Литтла.

В теории массового обслуживания рассматриваются разомкнутые и замкнутые СтМО.

Разомкнутые СтМО — это такие сети, в которых не зависит от количества заявок, уже находящихся в сети.

Замкнутой СтМО называется сеть, в которой зависит от количества заявок в сети.