Взаимодействие в гравитационном поле.

Гравитационное взаимодействие – одно из четырех фундаментальных взаимодействий в природе.

Гравитационные силы – силы взаимодействия, действующие между тяготеющими телами.

Закон всемирного тяготения: силы взаимного притяжения, действующие между двумя материальными точками, прямо пропорциональны массам этих точек и обратно пропорциональны квадрату расстояния между ними.

Формула для расчета силы гравитационного притяжения между двумя материальными точками:

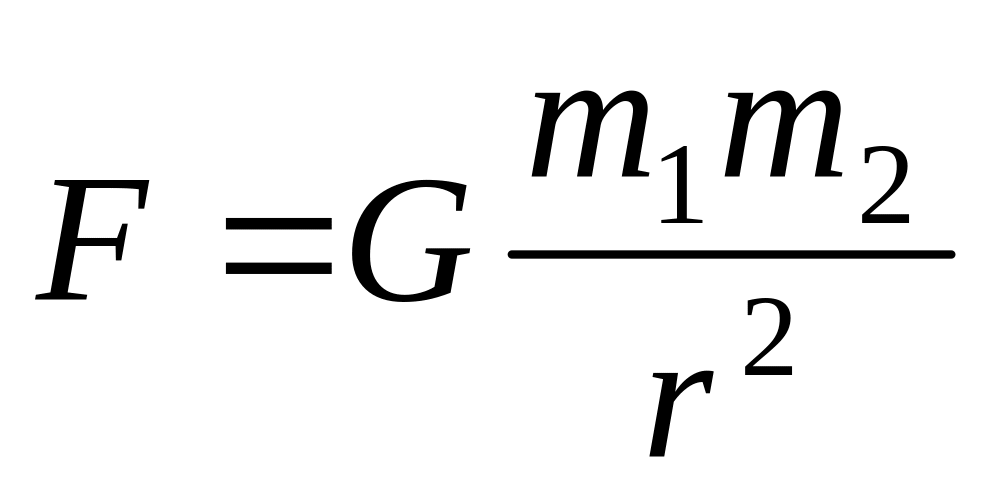, где m₁ и m₂ – массы материальных точек, r – расстояние между ними, G = 6,67  10^–11 Нм²/кг² – гравитационная постоянная.

Физическая сущность гравитационной постоянной: гравитационная постоянная численно равна силе взаимного притяжения двух материальных точек массой 1 кг на расстоянии 1 м.

Условия применения закона всемирного тяготения в виде

:

1) взаимодействие двух материальных точек; 2) взаимодействие тела произвольной формы с шаром, радиус которого значительно превосходит размеры тела (расстояние r в этом случае – длина отрезка между телом и центром шара); 3) взаимодействие двух шаров (расстояние r в этом случае – длина отрезка между центрами шаров).

Сила тяжести – сила, с которой Земля притягивает к себе тела.

Свободное падение – падение тел под действием только одной силы тяжести.

Ускорение свободного падения – ускорение тела при свободном падении (при падении тел вблизи поверхности Земли ускорение свободного падения составляет м/с²).

Зависимость ускорения свободного падения от высоты над поверхностью Земли:

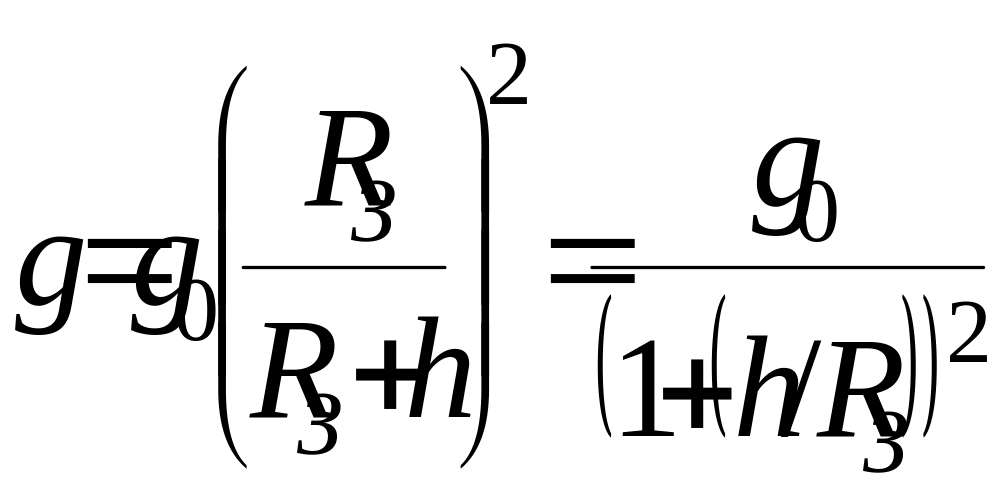, где м – радиус Земли, h – высота над поверхностью Земли.

Формула для расчета силы тяжести: ; .

Вес тела – сила, с которой тело действует на опору или растягивает подвес вследствие притяжения этого тела к Земле.

Отличия веса тела от силы тяжести:

Сила тяжести	Вес
1. Одна из составляющих силы тяготения, сообщающая ускорение свободно падающему телу.	1. Сила, с которой тело действует на опору или растягивает подвес.
2. Приложена к самому телу	2. Приложен к опоре или подвесу.
3. Направлена по линии отвеса в данном месте Земли.	3. Направление в каждом конкретном случае различно, в частности, может совпадать с направлением линии отвеса.
4. Величина, постоянная для данного места расположения тела и обусловленная тяготением Земли и ее суточным вращением вокруг оси.	4. Величина переменная, зависящая от ускорения движения тела и опоры (или подвеса) относительно Земли.
5. Сила гравитационная.	5. Сила упругости (электромагнитная сила).

Невесомость (отсутствие веса) – состояние, при котором тело и опора (подвес) движутся только под действием силы тяжести.

Перегрузка – состояние, при котором вес тела больше силы тяжести.

Коэффициент перегрузки (его часто называют просто перегрузкой) – отношение веса тела к силе тяжести ( ).

Движение тела под действием силы тяжести в случае, когда начальная скорость направлена по вертикали, является свободным падением (при подъеме и спуске).

Зависимость перемещения тела от времени: 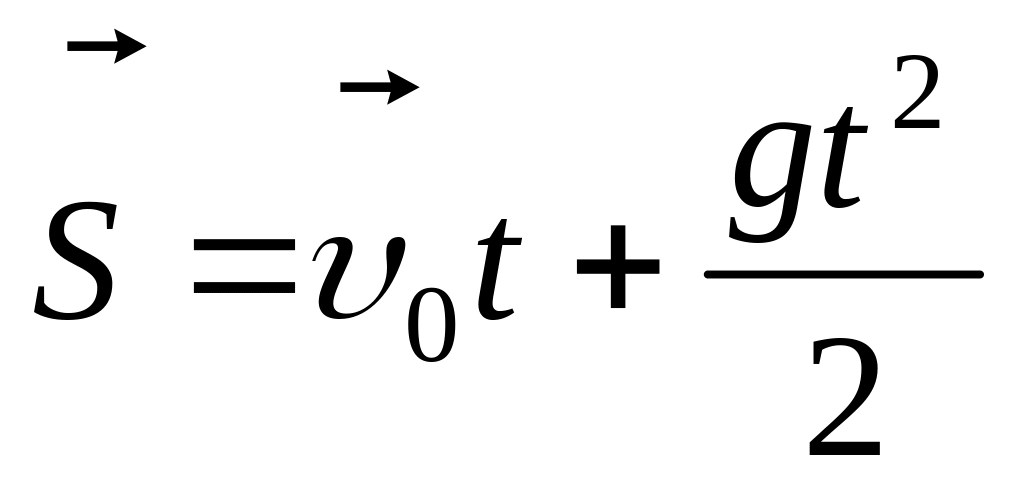, где – начальная скорость тела, – ускорение свободного падения.

Зависимость проекции перемещения тела на ось у от времени: .

Зависимость проекции перемещения тела от проекций конечной и начальной скорости тела и проекции ускорения свободного падения на ось у: 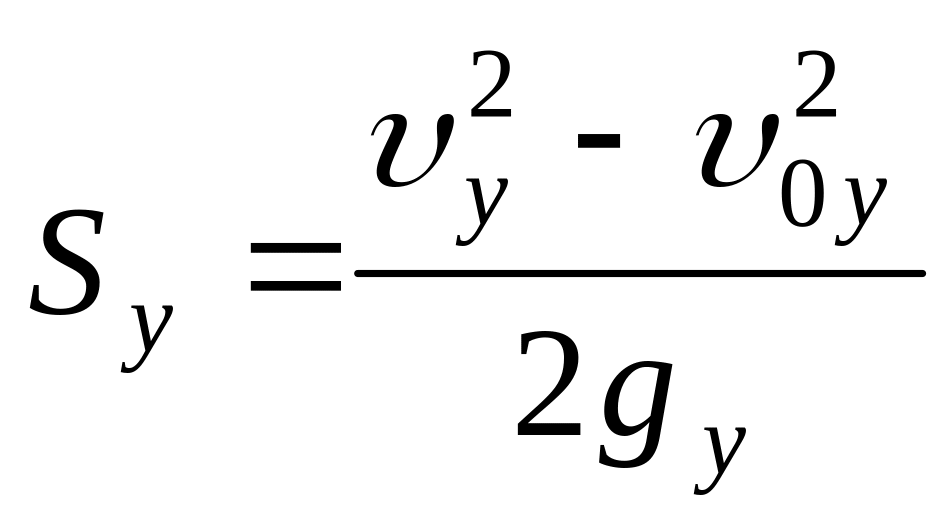, где – проекция конечной скорости тела на координатную ось у, – проекция начальной скорости на координатную ось у.

Зависимость скорости тела от времени: , где – начальная скорость тела, – ускорение свободного падения.

Зависимость проекции скорости тела на ось у от времени: .

Зависимость проекции скорости тела на ось у от проекции начальной скорости и проекции перемещения тела: ; .

Зависимость координаты тела от времени:

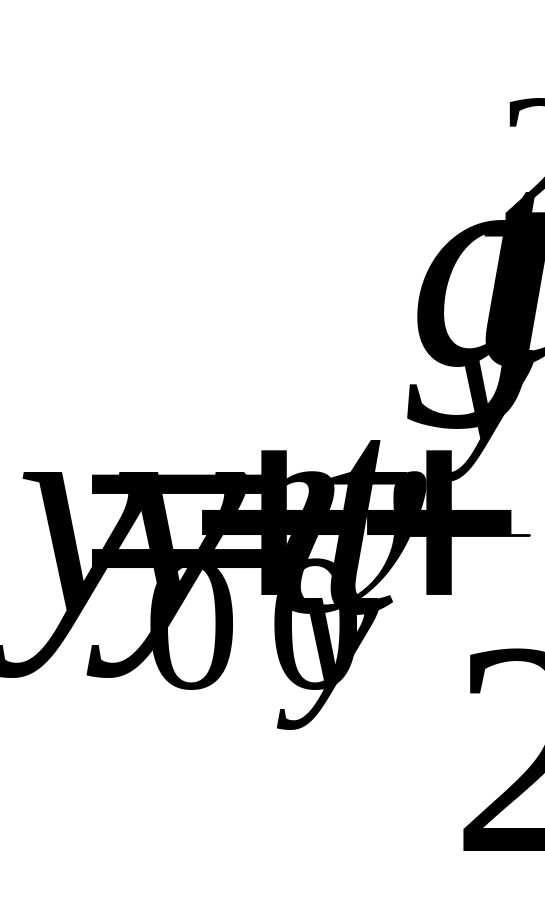, где – начальная координата тела; – проекция начальной скорости на координатную ось у; – проекция ускорения свободного падения на ось у.

Вид приведенных выше зависимостей зависит от выбора тела отсчета, направления координатной оси у и выбора начала отсчета на ней.

Движение тела, брошенного под углом к горизонту

Движение тела под действием силы тяжести в случае, когда начальная скорость направлена под углом к горизонту, является свободным падением.

Система отсчета, в которой удобно описывать этот тип движения: тело отсчета – земля; горизонтальная координатная ось х направлена вдоль горизонтальной составляющей начальной скорости тела, вертикальная координатная ось у направлена вверх; начало обеих координатных осей совмещено с точкой бросания тела; начало отсчета времени совпадает с моментом броска.

Вдоль горизонтальной координатной оси х тело движется прямолинейно равномерно со скоростью .

Вдоль вертикальной координатной оси у тело движется равноускоренно с ускорением и начальной скоростью .

Зависимость координаты х от времени: .

Зависимость координаты у от времени:

.

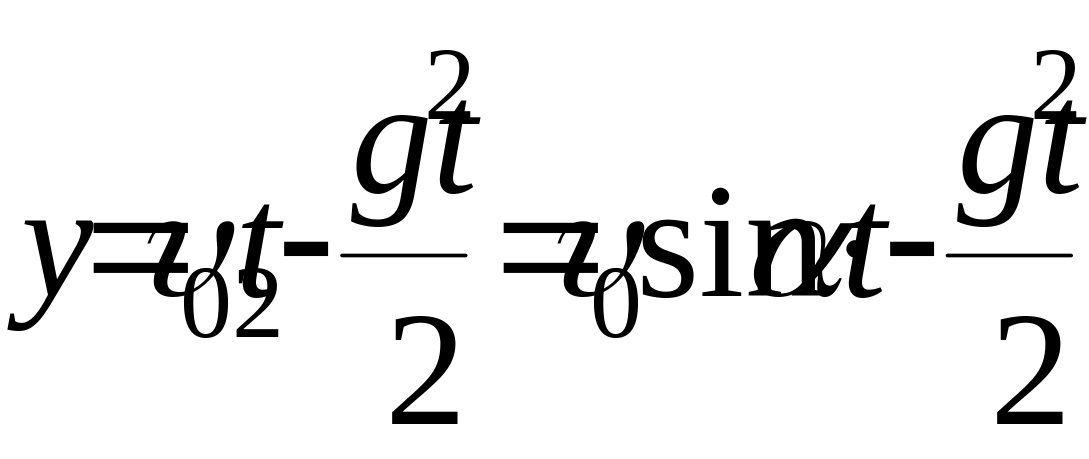Зависимость проекции перемещения тела на ось у от проекций на эту ось конечной и начальной скорости тела, а также ускорения свободного падения:

.

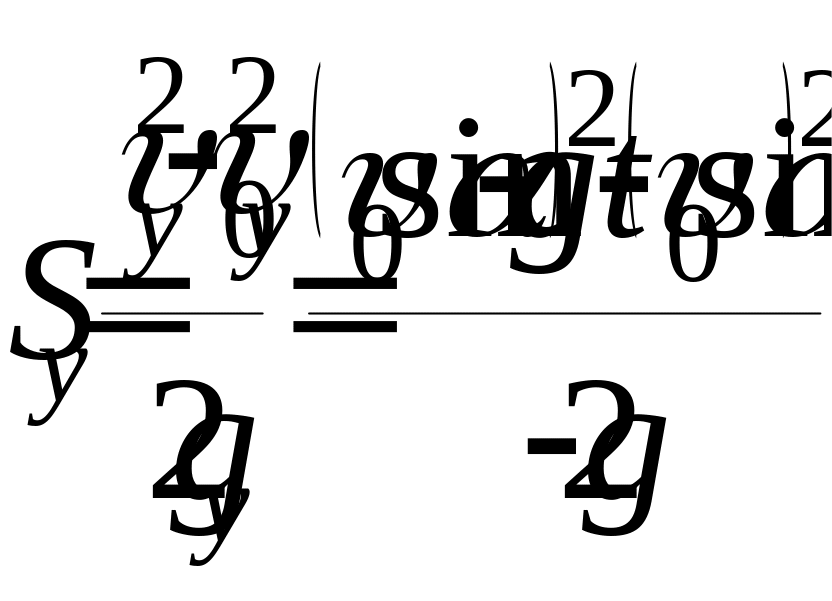
Зависимость скорости тела от времени: .

Зависимость проекции скорости тела на вертикальную координатную ось у от времени: .

Время движения тела от броска до падения на землю:

.

Время подъема тела на максимальную высоту:

.

Дальность полета тела в горизонтальном направлении:

.

Максимальная высота подъема тела: .

Уравнение траектории движения тела:

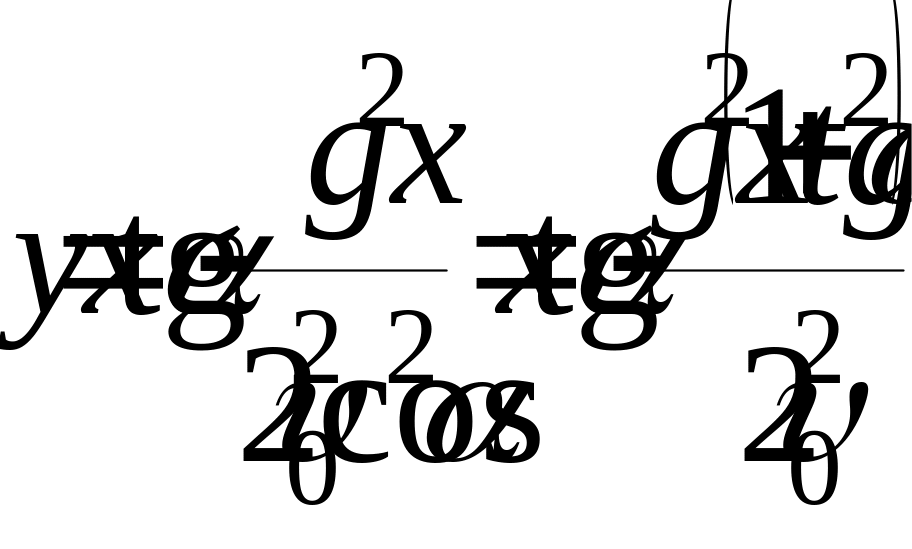– уравнение параболы.

Зависимость значения радиуса кривизны траектории от модуля скорости тела в данный момент времени или от самого времени t:

.

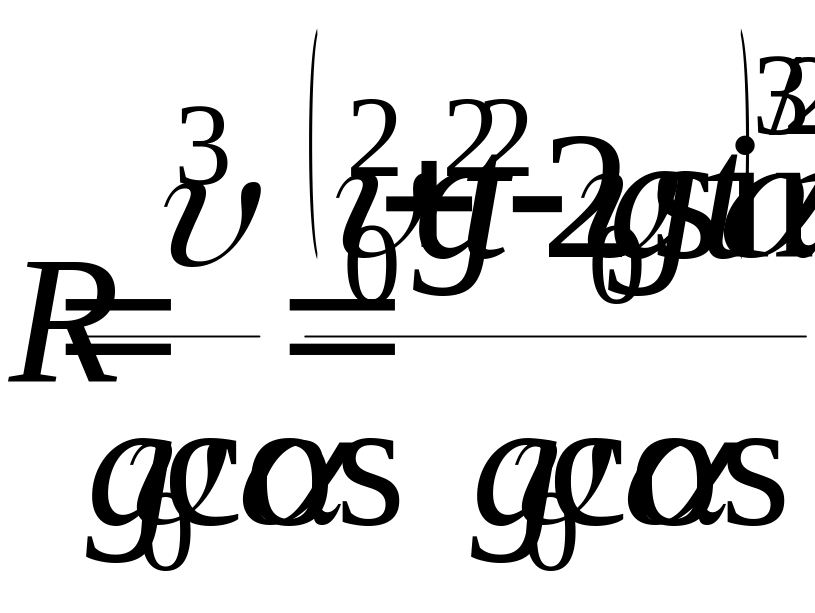Зависимость от времени угла наклона вектора скорости тела к горизонту:

;

.

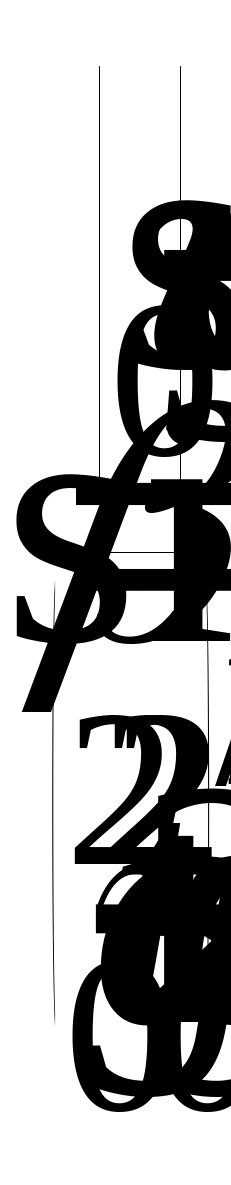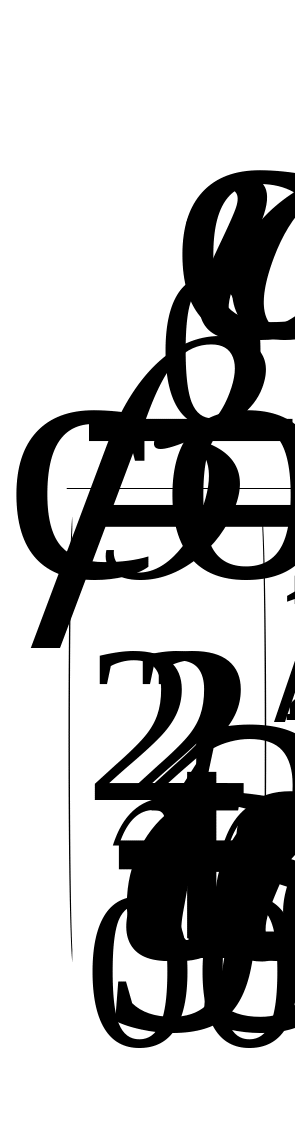Зависимость от времени значений тангенциального и нормального ускорения тела:

;

.
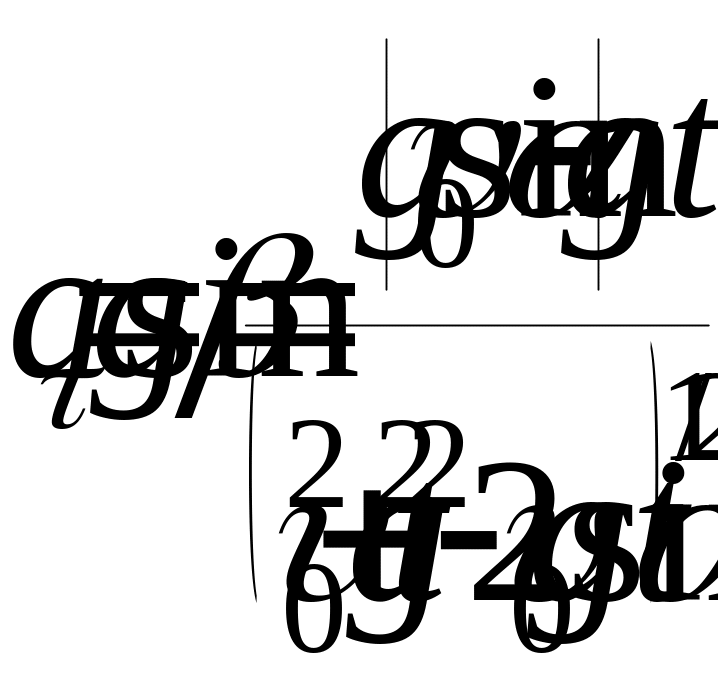
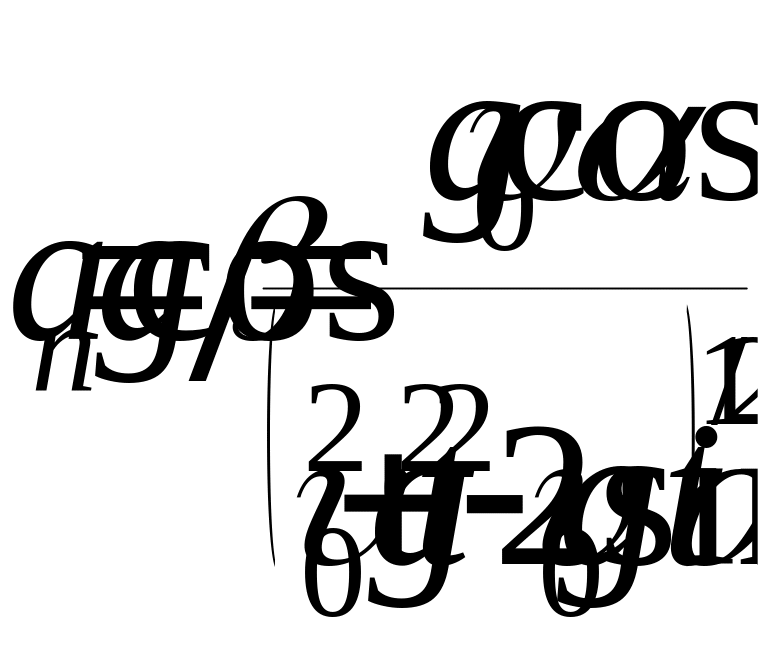