23. Посмотрим, как ведет себя диполь, попав во внешнее электрическое поле. Сначала — в однородное поле с напряженностью (рис. 3).

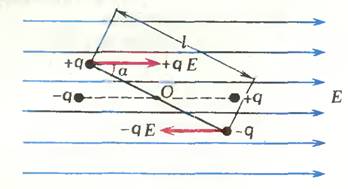
Рис. 3

На заряды диполя действуют равные по модулю, но противоположные по направлению силы   и  , которые стремятся развернуть диполь. Относительно оси, проходящей через центр диполя (точку О) и перпендикулярной плоскости чертежа, каждая сила создает вращающий момент, равный произведению модуля силы на соответствующее плечо (см. рис. 3):  .

Суммарный вращающий момент будет равен

 .

Таким образом, при заданных значениях Е и α вращающий момент М определяется величиной дипольного момента р.

Под действием вращающего момента диполь будет поворачиваться, пока не займет положение, изображенное на рисунке 3 штриховой линией. В этом положении равны нулю как сумма сил, так и сумма моментов сил, действующих на диполь. Это означает, что диполь находится в равновесии. При этом вектор электрического момента диполя сонаправлен с вектором напряженности поля.

Следовательно, в однородном внешнем электрическом поле диполь поворачивается и располагается так, чтобы его дипольный момент был ориентирован по полю. Заметим, что такое положение является положением его устойчивого равновесия.

Пусть теперь диполь находится в неоднородном внешнем поле. Разумеется, и здесь возникает вращающий момент, разворачивающий диполь вдоль поля (рис. 4). Но в этом случае на заряды действуют неодинаковые но модулю силы, равнодействующая которых отлична от нуля. Поэтому диполь будет еще и перемещаться поступательно, втягиваясь в область более сильного поля (убедитесь в этом самостоятельно).

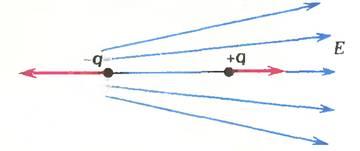
Рис. 4

24. Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью  . 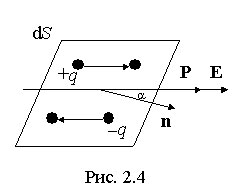Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 2.4). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью  , а на другой положительные заряды с плотностью  . С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами   и  , которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен  . С другой стороны, электрический момент единицы объема равен  , где  - угол, между направлением нормали к основанию призмы и вектором P. Произведение   есть объем призмы. Приравняв друг к другу оба выражения для электрического момента, получаем, что поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации:

,

где n - единичный вектор нормали к поверхности диэлектрика.

Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых  .