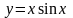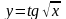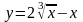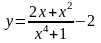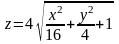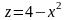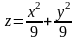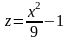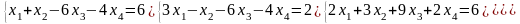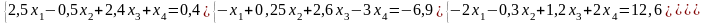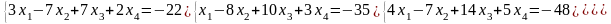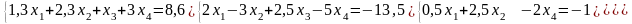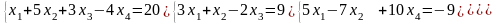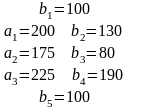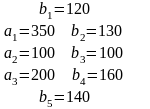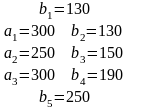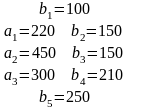Лабораторная работа 1.
Вычисление функции для заданных значений аргумента.
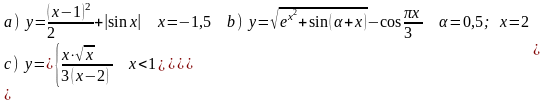
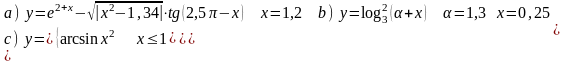
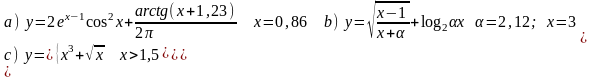
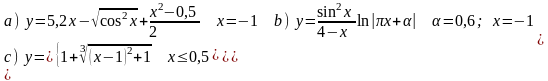
Вычислить значения функции y=f(x) на интервале для х [a, b] при изменении х с шагом h. Построить и форматировать график функции y=f(x).
№ |
|
|
№ |
|
|
|
|
|
[0; 15], 1,5 |
|
|
[0; 15], 1,5 |
|
|
|
[1,5 ;6,5], 0,5 |
|
|
[0; 15], 1,5 |
|
|
|
[0,1; 4,1], 0,4 |
|
|
[0; 5], 0,5 |
|
|
|
[0; 2], 0,2 |
|
|
[0; 1], 0,1 |
|
|
|
[0; 1], 0,1 |
|
|
[0,1; 1,1], 0,1 |
|
|
|
[0; 10], 1 |
|
|
[0; 5], 0,5 |
|
|
|
[0; 5], 0,5 |
|
|
[-5; 5], 1 |
|
|
|
[-4; 5], 1 |
|
|
[-3; 3], 0,5 |
|
|
|
[-5; 5], 1 |
|
|
[-2; 2], 0,5 |
|
|
|
[-2; 2], 0,5 |
|
|
[-1; 2], 0,2 |
|
|
|
[-4; 5], 1 |
|
|
[-2; 2], 0,5 |
|
|
|
[-4; 5], 1 |
|
|
[-2; 2], 0,5 |
|
|
|
[-2; 2], 0,5 |
|
|
[-2; 6], 1 |
|
|
|
[-2; 2], 0,4 |
|
|
[-5; 5], 1 |
|
|
|
[-2; 2], 0,5 |
|
|
[-1; 2], 0,2 |
Лабораторная работа 2.
Построить поверхность z=f(x,у) на интервале для х [a, b], у [c, d] при изменении х, y с шагом h.
№ |
|
|
№ |
|
|
1. |
|
[-4; 4], 0,5 |
16. |
|
[-5; 5], 1 |
2. |
|
[-5; 5], 1 |
17. |
|
[-4; 4], 0,5 |
3. |
|
[-4; 4], 0,5 |
18. |
|
[-5; 5], 1 |
4. |
|
[-5; 5], 1 |
19. |
|
[-4; 4], 0,5 |
5. |
|
[-4; 4], 0,5 |
20. |
|
[-4; 4], 0,5 |
6. |
|
[-5; 5], 1 |
21. |
|
[-5; 5], 1 |
7. |
|
[-4; 4], 0,5 |
22. |
|
[-5; 5], 1 |
8. |
|
[-4; 4], 0,5 |
23. |
|
[-5; 5], 1 |
9. |
|
[-5; 5], 1 |
24. |
|
[-4; 4], 0,5 |
10. |
|
[-5; 5], 1 |
25. |
|
[-5; 5], 1 |
11. |
|
[-4; 4], 0,5 |
26. |
|
[-4; 4], 0,5 |
12. |
|
[-4; 8], 1 |
27. |
|
[-4; 4], 0,5 |
13. |
|
[-4; 4], 0,5 |
28. |
|
[-4; 4], 0,5 |
14. |
|
[-5; 5], 1 |
29 |
|
[-5; 5], 1 |
15. |
|
[-4; 4], 0,5 |
30. |
|
[-4; 4], 0,5 |
Лабораторная работа 3.
Решение систем линейных уравнений:
а) методом Крамера;
б) метод обратной матрицы;
в) методом Гаусса
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лабораторная работа 4.
Решение задач линейного программирования
Транспортная задача
Имеются три пункта
поставки однородного груза
и пять пунктов
потребителя этого груза. На пунктах
находится груз соответственно
тонны. В пункты
требуется поставить соответственно
тонн груза. Расстояние
(стоимость перевозки) между пунктами
поставки и пунктами потребления
приводится в следующей таблице:
Пункты поставки |
Пункты потребления |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
|
А1 |
d11 |
d12 |
d13 |
d14 |
d15 |
А2 |
d21 |
d22 |
d23 |
d24 |
d25 |
А3 |
d31 |
d32 |
d33 |
d34 |
d35 |
Найти такое закрепление потребителей за поставщиками, чтобы затраты по перевозке груза были минимальными.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
