ЛАБОРАТОРНАЯ РАБОТА № 10

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

ИЗ КОЛЕБАНИЙ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МАЯТНИКОВ

Принадлежности: математический и физический маятники, секун­домер, линейка.

Цель работы: изучение законов колебательных движений на при­мере математического и физического маятников; определение ускорения свободного падения.

I. Гармонические колебания

Гармоническими колебаниями физической величины Х называется процесс изменения её во времени t по закону

где А - амплитуда колебания, Т - период колебания.

Величина носит название фазы, - начальной фазы.

График такого колебания представлен на рис.1.

Рис.1.

Из определения гармонического колебания следует, что период колебания является наименьшим промежутком времени, по истечении которого движение в точности повторяется. Действительно,

За время t = Т совершается одно полное колебание. Амплитуда колебания А равна максимальному значению X. Величина соответс­твует фазе в начальный момент времени (t = 0) и называется на­чальной фазой.

Величина

называется круговой (циклической) частотой. Если начальная фаза

равна = /2, то уравнение гармонического колебания записывается

в виде:

Х = А cos(wt) (2)

II. Математический маятник

Математическим маятником называется колебательная система, состоящая из материальной точки, прикреплённой к концу идеально гибкой, нерастяжимой и невесомой нити, второй конец которой зак­реплён неподвижно в точке подвеса и находится во взаимодействиис другими телами. Исследуемый в лабораторной установке маятник схематически изображён на рис.2. Он представляет собой сталь­ной шарик радиусом r на бифилярном подвесе: тонкая нить пропущена через центр шарика, концы нити зак­реплены на стойке. Длина подвеса L может регулироваться в пределах от нескольких сантиметров до 0.5 м.

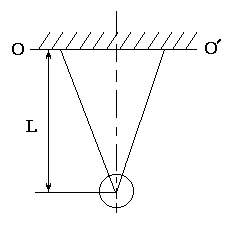
Момент инерции маятника складывается из момента инерции ша­рика и момента инерции нити подвеса относительно оси OO'. Пренеб­регая моментом инерции нити, запишем момент инерции маятника от­носительно оси ОО' в виде:

J_o = J_c + mL² = 2/5 mr² + mL² . (3)

Соотношение (3) следует из теоремы Гюйгенса-Штейнера, если учесть, что момент инерции однородного шара радиусом r и массой m относительно оси, проходящей через его центр, равен

J_c = 2/5 mr² .

Рассмотрим случай, когда радиус шарика мал по сравнению с длиной подвеса: r << L .Тогда в (3) можно пренебречь слагаемым

2/5 Mr2, малым по сравнению с mL2, и положить

J_o = mL² . (4)

В этом приближении J определяется, очевидно, с небольшой систе­матической погрешностью: (5)

которую в условиях опыта легко оценить. С учётом (4) период коле­баний маятника можно записать в виде:

₍₆₎

Из формулы (6) следует, что период колебаний математического маятника не зависит от его массы m. Заметим, что формула (6) справедлива лишь для малых углов. Более точная формула для опре­деления периода имеет вид:

_(6')

Длиной маятника является расстояние от центра тяжести до точки подвеса. Центр тяжести лабораторного маятника не совпадает

точно с геометрическим центром тяжести шарика, поэтому непосредс­твенное измерение длины не представляется возможным. При опреде­лении ускорения силы тяжести рассматривают колебания маятника для разных его длин.

Если определить периоды колебаний двух маятников с различны­ми длинами, то согласно формуле (6) можно записать:

₍₇₎

Откуда определяем

(8)

Таким образом, для того, чтобы определить ускорение силы тя­жести, достаточно знать длину математического маятника и соот­ветствующий период колебаний в двух опытах.

III. Измерения.

а). Выполнение работы на электрофицированной установке:

1. Нижний кронштейн вместе с фотоэлектрическим датчиком ус­тановить в нижней части колонки, обращая внимание на то, чтобы верхняя грань кронштейна показывала на шкале длину не меньше 50 см. Зафиксировать фотоэлектрический датчик в избранном положении.

Поворачивая верхний кронштейн, поместить над датчиком мате­матический маятник.

Вращая вороток на верхнем кронштейне установить выбранную длину математического маятника. Обратить внимание на то, чтобы черта на шарике была продолжением черты на корпусе фотоэлектри­ческого датчика, стопорным винтом зафиксировать выбранную длину.

Привести математический маятник в движение, отклонив шарик на 4-5^o от положения равновесия.

Нажать кнопку <СБРОС>.

После подсчёта измерителем N колебаний ( N=10_20 ) нажать

кнопку <СТОП>.

Время t измеряется не менее 5 раз и вычисляется ошибка изме­рений. Для данной длины отмечают положение нижнего края шарика по шкале - n₁.

2. Поднять шарик на несколько см, укорачивая нить, и закре­пить её стопорным винтом. По шкале определить положение нижнего края шарика - n₂. Измерить период колебаний маятника Т₂.

3. По формуле 9 определить периоды колебаний математического маятника для данных длин L₁ и L₂ .

Т = t/N (9)

4. Ускорение силы тяжести вычислить по формуле (8). Найти

ошибку определения величины g. Разность отсчётов n₂ - n₁ по шкале

даёт L₂ - L₁. Необходимо помнить, что углы отклонения маятника

должны быть малыми.

б). Выполнение работы на установке не оборудованной фотоэ­лектрическим датчиком:

1. Установить выбранную длину маятника.

2. Отклонить шарик от положения равновесия на угол 4-5^о. Отпустить шарик, включив одновременно секундомер. После подсчета 10 - 20 колебаний, выключить секундомер. Измерение времени коле­баний произвести не менее 5 раз и вычислить ошибку. Вычислить Т₁.

3. Поднять шарик на несколько см., укорачивая нить. Повто­рить п.1-2. Вычислить Т₂.

4. Ускорение силы тяжести найти по формуле (8). Определить ошибку измерений.

mex10-3.pcx 5 60

IV. Физический маятник.

Физическим маятником называется тело, укреплённое на непод­вижной горизонтальной оси, не проходящей через его центр тяжести, и способное совершать колебания относительно этой оси (рис.3). Покажем, что маятник, отклонённый на малый угол a от положения равновесия, будет совершать гармонические колебания и найдем период колебаний такого маятника. Обозначим через J момент инерции маятника относительно оси О. Пусть точка C является центром тяжести. Силу тяжести F = mg можно разложить на две составляющие, одна из которых - F₂, уравновешивается реакцией опоры. Под действием другой составляющей маятник приходит в движение:

Рис.3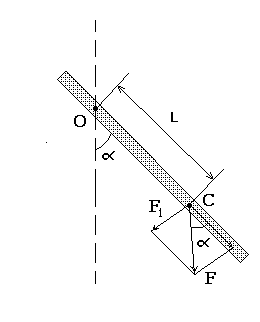

F₁ = Fsinα (10)

На основании второго закона Ньютона для вращательного дви­жения ( М = Jβ ) имеем:

Jβ = - F₁L, (11)

где угловое ускорение равно:

L = CО - расстояние от точки подвеса до центра тяжести. Знак ми­нус выбран потому, что момент силы М стремится вернуть маятник в положение равновесия, т.е. уменьшить угол a. Т.к. угол α мал, то sina ~ α и

F₁ = mga . (13)

Подставляя (12) и (13) в уравнение (11) получим,

(14)

Частным решением последнего дифференциального уравнения яв­ляется:

α = А cos (wt), (15)

где

w = (16)

A - амплитуда колебаний маятника.

Дважды дифференцируя (15), получим:

(17)

Подставляя (15) и (17) в (14), можно убедиться, что левая часть уравнения тождественно равна нулю.

Сравнивая (16) и (1), получим:

T = (18)

Из уравнения (18) следует, что период колебания увеличивается с увеличением момента инерции.