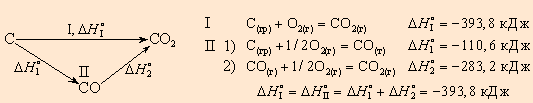4.4. Закон Гесса

Пользуясь табличными значениями и , можно рассчитать энтальпии различных химических процессов и фазовых превращений. Основанием для таких расчетов является закон Гесса, сформулированный петербургским профессором Г. И. Гессом (1841 г.): «Тепловой эффект (энтальпия) процесса зависит только от начального и конечного состояния и не зависит от пути перехода его из одного состояния в другое».

Анализ закона Гесса позволяет сформулировать следующие следствия:

1. Энтальпия реакции равна разности сумм энтальпий образования конечных и начальных участников реакций с учетом их стехиометрических коэффициентов.

   ΔH = ΣΔHобр.конечн – ΣΔHобр.нач

2. Энтальпия реакции равна разности сумм энтальпий сгорания начальных и конечных реагентов с учетом их стехиометрических коэффициентов.

   ΔH = ΣΔHсгор.нач – ΣΔHсгор.конечн

3. Энтальпия реакции равна разности сумм энергий связей E_св исходных и конечных реагентов с учетом их стехиометрических коэффициентов.

В ходе химической реакции энергия затрачивается на разрушение связей в исходных веществах (ΣE_исх) и выделяется при образованиии продуктов реакции (–ΣE_прод). Отсюда

ΔH° = ΣEисх – ΣEпрод

Следовательно, экзотермический эффект реакции свидетельствует о том, что образуются соединения с более прочными связями, чем исходные. В случае эндотермической реакции, наоборот, прочнее исходные вещества.

При определении энтальпии реакции по энергиям связей уравнение реакции пишут с помощью структурных формул для удобства определения числа и характера связей.

Энтальпия реакции образования вещества равна энтальпии реакции разложения его до исходных веществ с обратным знаком.

ΔHобр =  –ΔHразл

Энтальпия гидратации равна разности энтальпий растворения безводной соли и кристаллогидрата

Из вышесказанного видно, что закон Гесса позволяет обращаться с термохимическими уравнениями как с алгебраическими, т. е. складывать и вычитать их, если термодинамические функции относятся к одинаковым условиям.

Например, диоксид углерода можно получить прямым синтезом из простых веществ (I) или в две стадии через промежуточный продукт (II):

Рисунок 4.1. Энтальпия первого пути равна сумме энтальпий отдельных стадий второго пути.

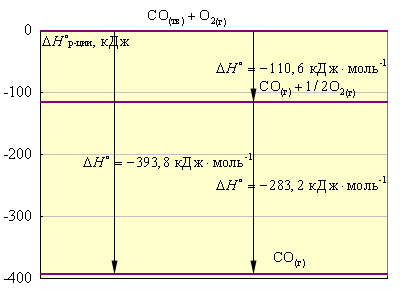
Эти термохимические реакции можно представить в виде энтальпийных диаграмм. Естественно, за начало следует принять стандартные состояния простых веществ, энтальпии которых равны нулю. Образование сложных веществ (CO и CO₂) сопровождается понижением энтальпии системы.

Рисунок 4.2. Энтальпийная диаграмма C + O2.

4.5. Энтропия

Изменение энтальпии системы не может служить единственным критерием самопроизвольного осуществления химической реакции, поскольку многие эндотермические процессы протекают самопроизвольно. Иллюстрацией этого служит растворение некоторых солей (например, NH₄NO₃) в воде, сопровождающееся заметным охлаждением раствора. Необходимо учитывать еще один фактор, определяющий способность самопроизвольно переходить из более упорядоченного к менее упорядоченному (более хаотичному) состоянию.

Энтропия (S) – термодинамическая функция состояния, которая служит мерой беспорядка (неупорядоченности) системы. Возможность протекания эндотермических процессов обусловлена изменением энтропии, ибо в изолированных системах энтропия самопроизвольно протекающего процесса увеличивается ΔS > 0 (второй закон термодинамики).

Л. Больцман определил энтропию как термодинамическую вероятность состояния (беспорядок) системы W. Поскольку число частиц в системе велико (число Авогадро N_A = 6,02∙10²³), то энтропия пропорциональна натуральному логарифму термодинамической вероятности состояния системы W:

S = R · ln W

Размерность энтропии 1 моля вещества совпадает с размерностью газовой постоянной R и равна Дж∙моль^–1∙K^–1. Изменение энтропии ^*) в необратимых и обратимых процессах передается соотношениями ΔS > Q / T и ΔS = Q / T. Например, изменение энтропии плавления равно теплоте (энтальпии) плавления ΔS_пл = ΔH_пл/T_пл Для химической реакции изменение энтропии аналогично изменению энтальпии

^*) термин энтропия был введен Клаузиусом (1865 г.) через отношение Q/T (приведенное тепло).

Здесь ΔS^° соответствует энтропии стандартного состояния. Стандартные энтропии простых веществ не равны нулю. В отличие от других термодинамических функций энтропия идеально кристаллического тела при абсолютном нуле равна нулю (постулат Планка), поскольку W = 1.

Энтропия вещества или системы тел при определенной температуре является абсолютной величиной. В табл. 4.1 приведены стандартные энтропии S^° некоторых веществ.

Соединение (Дж∙моль–1∙K–1) Соединение (Дж∙моль–1∙K–1) C(т)алмаз 2,37 NO(г) 210 C(т)графит 5,74 NO2(г) 240 H2(г) 131 N2O5(г) 342 D2(г) 145 H2O(г) 189 O(г) 161 H2O(ж) 70 O2(г) 205 D2O(ж) 79 O2(ж) 84 CH4(г) 186 O2(т) 42 C2H6(г) 229 O3(г) 237 н-C4H10(г) 310     изо-C4H10(г) 294

Таблица 4.1. Стандартные энтропии некоторых веществ.

Из табл. 4.1 следует, что энтропия зависит от:

1. Агрегатного состояния вещества. Энтропия увеличивается при переходе от твердого к жидкому и особенно к газообразному состоянию (вода, лед, пар).

2. Изотопного состава (H₂O и D₂O).

3. Молекулярной массы однотипных соединений (CH₄, C₂H₆, н-C₄H₁₀).

4. Строения молекулы (н-C₄H₁₀, изо-C₄H₁₀).

5. Кристаллической структуры (аллотропии) – алмаз, графит.

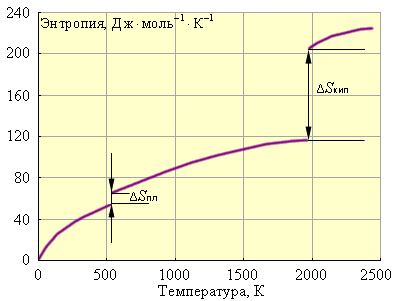
Наконец, рис. 4.3 иллюстрирует зависимость энтропии от температуры.

Рисунок 4.3. Зависимость энтропии от температуры для свинца: ΔSпл = 8 Дж·моль–1·К–1; Tпл = 600,5 К; ΔSкип = 88 Дж·моль–1·К–1; Tкип = 2013 К.

Следовательно, стремление системы к беспорядку проявляется тем больше, чем выше температура. Произведение изменения энтропии системы на температуру TΔS количественно оценивает эту тендецию и называется энтропийным фактором.