Циклы пересчета

Переход от одного опорного плана к другому в транспортной задаче сводится к тому, что, как и в симплекс-методе, надо ввести в базис новый вектор вместо выведенного базисного вектора. Это способствует тому, что одну из свободных клеток мы сделаем занятой, т.е. базисной, а одну из базисных – свободной.

Пусть первоначальный опорный план задан таблицей

Пункты отправления	Пункты назначения				Предложение
	В1	В2	В3	В4
1	2	3	4	5	6
А1	20 5	10 4	2	5	30
А2	6	70 1	1	3	70
А3	2	10 3	40 1	8	50
А4	6	3	30 2	70 1	100
Спрос	20	90	70	70

Выберем одну из свободных клеток, например (4,1), и поместим в нее некоторую положительную величину перевозки . Поскольку число занятых клеток должно быть равно m + n - 1, то какую-то из занятых клеток необходимо освободить. Чтобы получить новый опорный план, необходимо пересчитать значения базисных переменных. Для того, чтобы сумма перевозок в первом столбце не изменилась, нужно перевозку Х₁₁ = 20 уменьшить на величину . Для того, чтобы при этом не изменилась сумма перевозок в первой строке, надо перевозку Х₁₂ = 10 увеличить на  и т.д. Пересчет продолжается, пока мы не вернемся к тому значению , с которого начали, т.е. не замнем цикл пересчета:

Пункты отправления	Пункты назначения				Предложение
	В1	В2	В3	В4
А 1	20 -  5	10 +  4	2	5	30
А2	6	70 1	1	3	70
А 3	2	10 -  3	40 +  1	8	50
А 4	 6	3	30 -  2	70 1	100
Спрос	20	90	70	70	-

Данная операция называется сдвигом по циклу пересчета на величину . Значение  выбирается равным наименьшему из тех перевозок, из которых  вычитается. В нашем примере выбирается  = 10; если взять  > 10, то перевозка Х₃₂ станет меньше нуля, а если взять  < 10, то получим больше, чем m+n-1 отличную от нуля перевозку, т.е. новый план тогда не будет опорным.

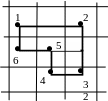
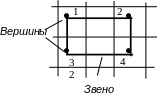
Переход от одного опорного плана к другому связан с некоторым обходом по замкнутой ломаной линии, начало которой находится в свободной клетке, а все остальные вершины в некоторых базисных (занятых) клетках. Если ломаная линия, образующая цикл, пересекается сама с собой, то точки пересечения не являются вершинами. Циклы могут быть различной формы: Вершин в цикле всегда четное число. Цикл, одна из вершин которого лежит в свободной клетке, а все остальные – в базисных, называется циклом пересчета данной свободной клетки.

Каждый опорный план обладает следующими свойствами:

1) не существует циклов, все вершины которых лежат в базисных клетках;

2) для каждой свободной клетки существует единственный цикл пересчета.

В общем случае, для того чтобы определить , припишем каждой вершине цикла определенный знак таким образом, чтобы две соседние вершины имели противоположные знаки, а вершина, лежащая в свободной клетке, была всегда положительна, т.е. приписываем ей знак (+). Поскольку число вершин в цикле четное, то число положительных вершин будет равно числу отрицательных. При сдвиге по циклу пересчета на величину  перевозки в положительных вершинах цикла увеличиваются на величину , а в отрицательных – уменьшаются на . Следовательно, величину  надо выбирать равной наименьшей из перевозок в отрицательных вершинах:

Пункты отправления	Пункты назначения				Предложение
	В1	В2	В3	В4
А 1	20 5 -	10 4 +	2	5	30
А2	6	70 1	1	3	70
А 3	2	10 3 -	+ 40 1	8	50
А 4	 6 +	3	- 30 2	1	100
Спрос	20	90	70	70	-

Определим, как изменится функция цели (стоимость перевозок) при переходе к новому опорному плану:

+  6 -   5 +   4 -   3 +   1 -   2 =  (6 – 5 + 4 – 3 + 1 - 2) = +  1.

Следовательно, функция цели увеличится на величину , а значит, клетка (4,1) для новой перевозки выбрана неудачно: f(x) = 410 +  = 410 + 10 = 420 ден.ед.

Для того чтобы перейти к лучшему опорному плану, с меньшей функцией цели, можно воспользоваться распределительным методом решения транспортных задач.