Условие неотрицательности решения

x_j  0, (j = ).

4. Задача составления оптимальной смеси (задача диеты)

Для производства продукции используется n различных материалов, включающих в себя ряд различных компонентов (ингридиентов, элементов). Качество продукции определяется содержанием в ней различных компонентов в определенном количестве (никак не меньшем). Известны коэффициенты а_ij – удельный вес i–го компонента в единице j–го исходного материала; b_i- необходимое содержание i–го элемента в смеси; C_j - цена единицы j–го материала.

Компоненты, входящие в состав материалов	Виды материалов	Необходимое количество компонентов в смеси (продукции)
	1 … j … n
1 … i … m	а11 … а1j … а1n ………………… аi1 … аij … аin ………………… аm1 … аmj … аmn	b1 … bi … bm
Цена единицы материала	С1 … Сj … Сn	__

Обозначим через Х_j количество j–го материала, входящего в смесь (в готовый продукт).

Тогда

а₁₁  x₁ + … + а_1j  x_j +…+ а_1n  x_n  b₁,

………………………………………

а_i1  x₁ + …+ а_ij  x_j + … + а_in  x_n  b₂,

………………………………………

а_m1  x₁ + … + а_mj  x_j + … + а_mn  x_n  b_m.

Функция цели – минимальные затраты на материалы

f(x) = C₁  x₁ + …+ C_j  x_j + …+ C_n  x_n  min.

Условие неотрицательности решения x_j  0, (j = ).

5. Распределительная задача: о размещении парка оборудования по участкам производства

Имеется n типов оборудования, которое должно быть использовано на m участках. Известно: число единиц оборудования каждого j–го типа (d_j); производительность оборудования j–го типа на i–м участке (а_ij); затраты на эксплуатацию единицы оборудования j–го типа на i–м участке (C_ij). Задан объем работы, который необходимо выполнить на каждом участке (b_i). Требуется так распределить парк оборудования, чтобы расходы на эксплуатацию были бы минимальными.

Пусть Х_ij – число единиц оборудования j–го типа, которое направляется на i–й участок.

Участки производства	Виды оборудования	Объем работы
	1 … j … n
1 … i … m	аij \ Сij	b1 … bi … bm
Наличие оборудования	d1 … dj … dn	__

Все оборудование должно быть распределено по участкам

Х₁₁ + … + Х_i1 +…+ X_m1 = d₁,_{_}

……………………………..

Х_1j + … + Х_ij +…+ X_mj = d_j,

……………………………..

Х_1n + … + Х_in +…+ X_mn = d_n.

Работа должна быть выполнена (и, если возможно, перевыполнена)

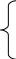а₁₁  x₁₁ + … + а_1j  x_1j +…+ а_1n  x_1n  b₁,

……………………………………………

а_i1  x_i1 + …+ а_ij  x_ij + … + а_in  x_in  b_i,

……………………………………………

а_m1  x_m1 + … + а_mj  x_mj + … + а_mn  x_mn  b_m.

Расходы на эксплуатацию оборудования должны быть минимальными

f(x) = C₁₁  x₁₁ + …+ C_ij  x_ij + …+ C_mn  x_mn  min.