
- •II. Квадратичные по полю эффекты при взаимодействии фемтосекундных оптических импульсов с материальными средами
- •2.4. Параметрическая генерация и усиление фемтосекундных импульсов [1-6]
- •Что такое параметрическая генерация и усиление электромагнитных волн? [1, 2]
- •Параметрическое усиление в поле чирпованной накачки
II. Квадратичные по полю эффекты при взаимодействии фемтосекундных оптических импульсов с материальными средами
2.4. Параметрическая генерация и усиление фемтосекундных импульсов [1-6]
Что такое параметрическая генерация и усиление электромагнитных волн? [1, 2]
Под параметрической генерацией и усилением электромагнитных волн понимается генерация и усиление за счет работы, совершаемой внешним источником при периодическом изменении реактивных параметров колебательной системы, например, при периодическом изменении емкости или индуктивности колебательного контура.
В
основе явления – параметрический
резонанс, раскачка колебаний контура
при изменении его реактивных параметров
с частотой
![]() ,
кратной собственной частоте контура
ω0:
,
кратной собственной частоте контура
ω0:
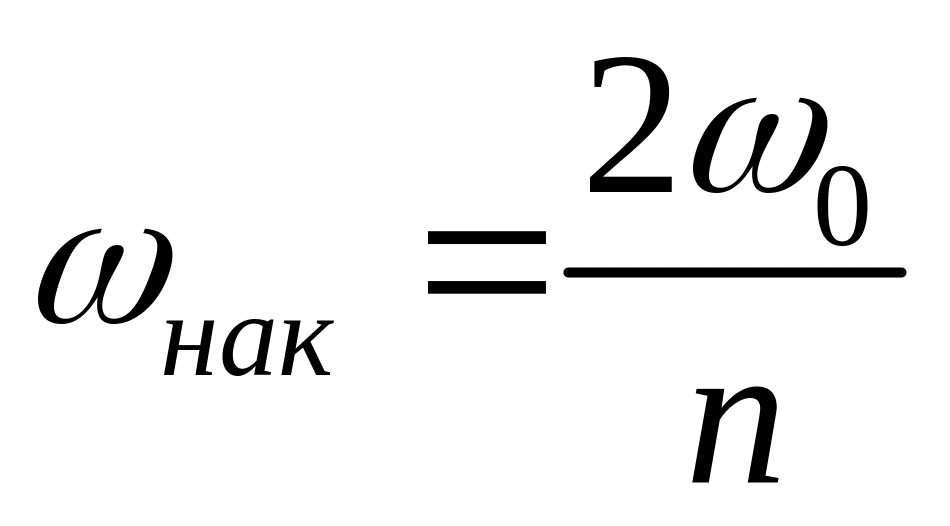 ,
где n
-
целое число.
(2.84)
,
где n
-
целое число.
(2.84)
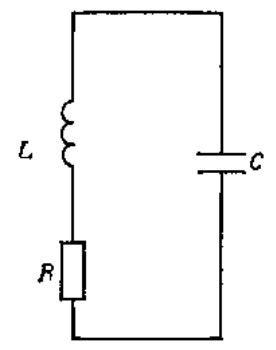
Рис.2. 40. «Машина Мандельштама-Папалекси». Демонстрационные эксперименты в МГУ 1930-33 гг. [1].
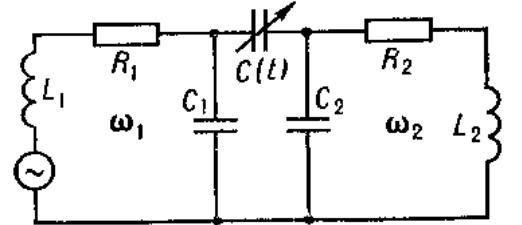
Рис.2.
41. Двухконтурный параметрический
усилитель: частоты контуров удовлетворяют
условию
![]() ,при
этом
,при
этом
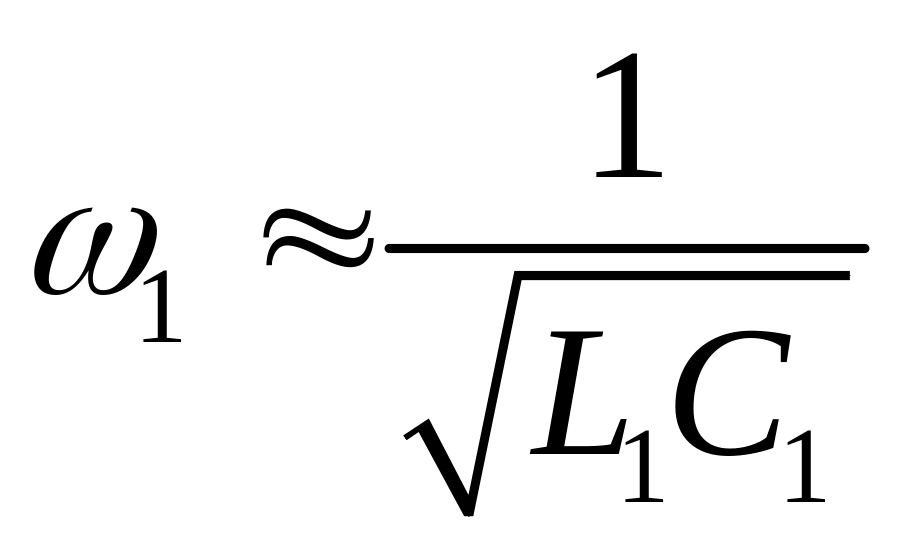 и
и
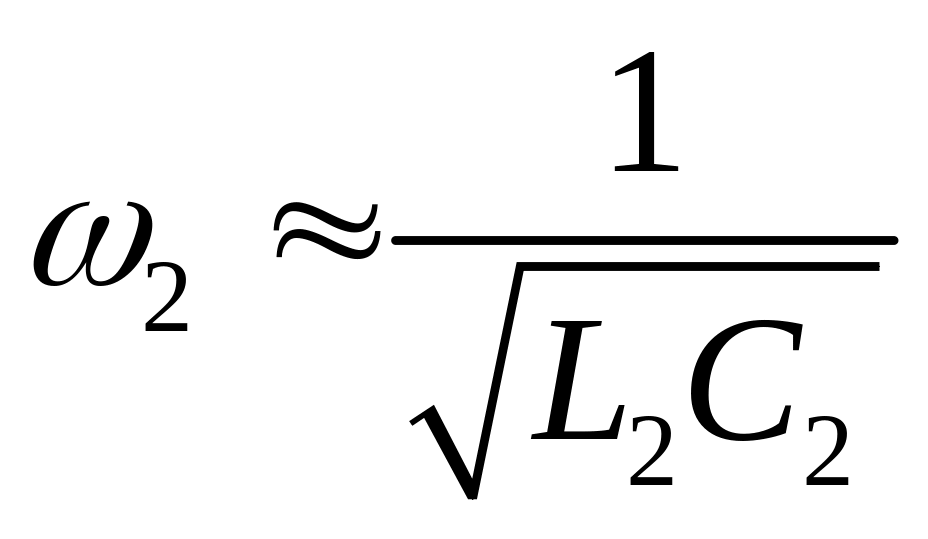 .
Один контур настроен на частоту входного
сигнала, второй - на
.
Один контур настроен на частоту входного
сигнала, второй - на
![]() [2].
[2].
В
оптике параметрическая раскачка
собственных колебаний среды происходит
под действием электрического поля волны
накачки
![]() ,
которая модулирует диэлектрическую
проницаемость
,
которая модулирует диэлектрическую
проницаемость
![]() среды с квадратичной восприимчивостью
среды с квадратичной восприимчивостью![]() :
:
![]() (2.85)
(2.85)
где
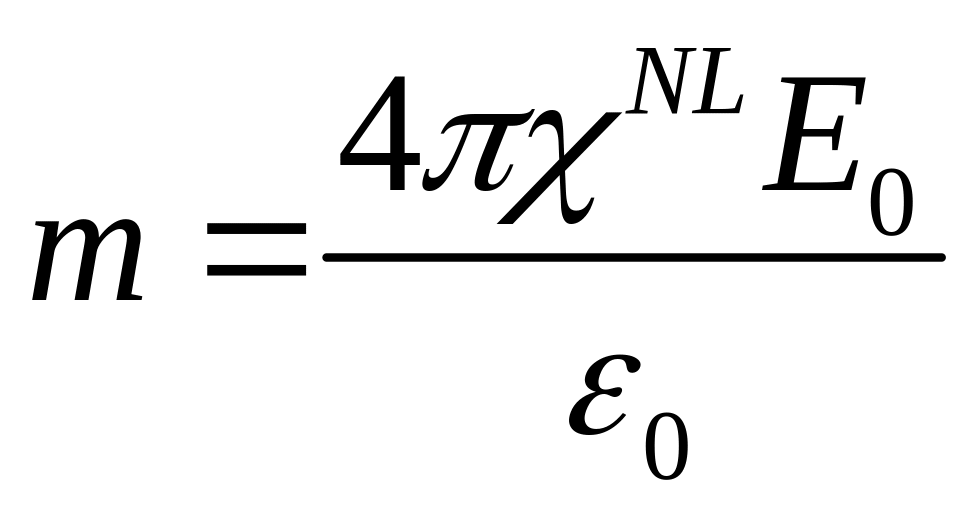 -
глубина модуляции.
-
глубина модуляции.
При этом поляризация в среде представляется в виде
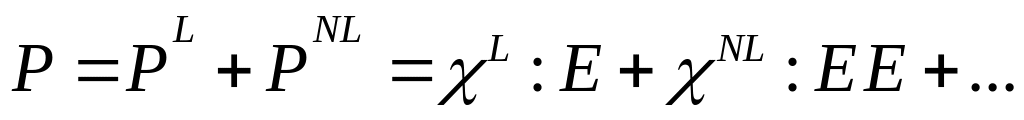 (2.86)
(2.86)
В
результате из шума усиливаются колебания
с частотами
![]() ,
связанные с частотой накачки
,
связанные с частотой накачки
![]() (
(![]() )
соотношением:
)
соотношением:
![]() (2.87)
(2.87)
Для эффективной передачи энергии от волны накачки к возбуждаемым волнам необходимо согласование их фазовых скоростей, которое достигается при выполнении фазового синхронизма.
Для волновых векторов волн условие синхронного взаимодействия или фазового согласования имеет вид:
![]() (2.88)
(2.88)
Таким
образом, оптический параметрический
процесс в нелинейной среде можно
трактовать как возбуждение бегущей
волной с частотой
и волновым вектором k3
двух
бегущих волн с частотами
![]() и
и
![]() и волновыми векторами k1
и k2
, если выполняются условия параметрического
резонанса во времени и в пространстве
(2.87-2.88).
и волновыми векторами k1
и k2
, если выполняются условия параметрического
резонанса во времени и в пространстве
(2.87-2.88).
С другой стороны параметрический процесс можно представить, как распад фотона высокой частоты 3 (p) на пару фотонов с более низкими частотами 1 (s - частота сигнальной волны) и 2 (I - частота холостой волны), при этом принято s >i.
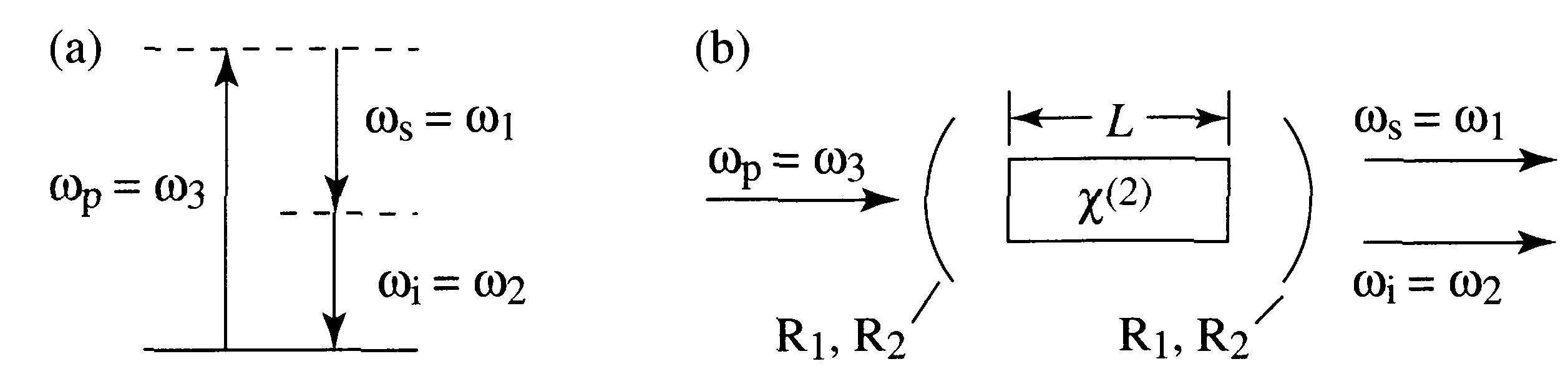
Рис. 2.42. а- параметрический процесс, б- параметрический генератор
Режим параметрической генерации или усиления, при котором
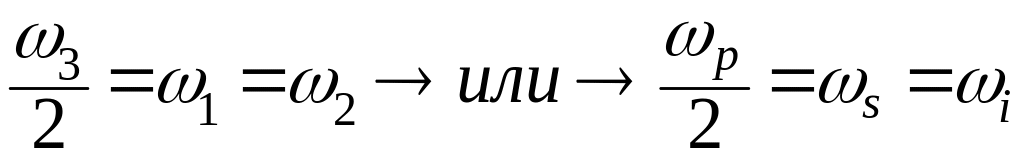 ,
(2.89)
,
(2.89)
называется вырожденным или режимом генерации субгармоники.
Для упрощения анализа параметрического взаимодействия обычно вводится параметр вырождения
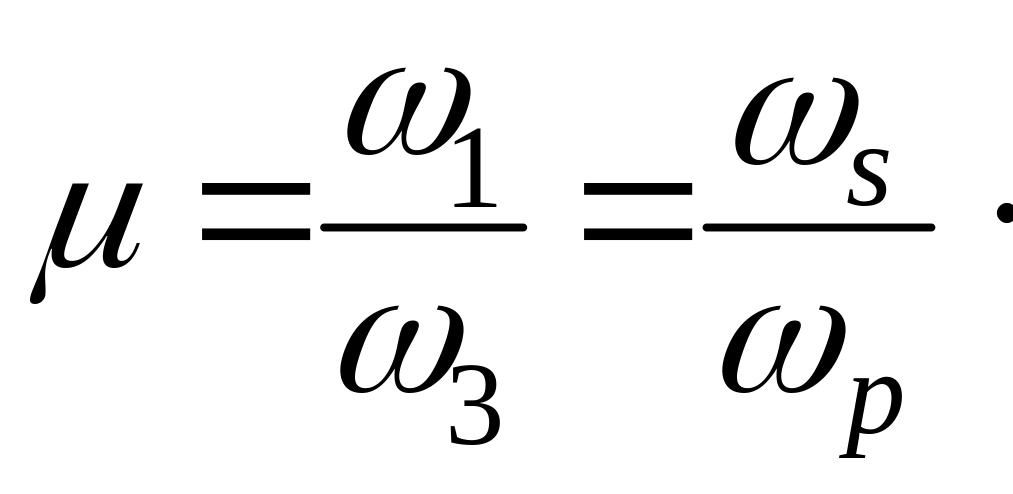 (2.90)
(2.90)
Согласно правилу, полученному для параметрических генераторов радиодиапазона, между мощностями волн, участвующими в процессе, должно выполняться соотношение Мэнли-Роу:
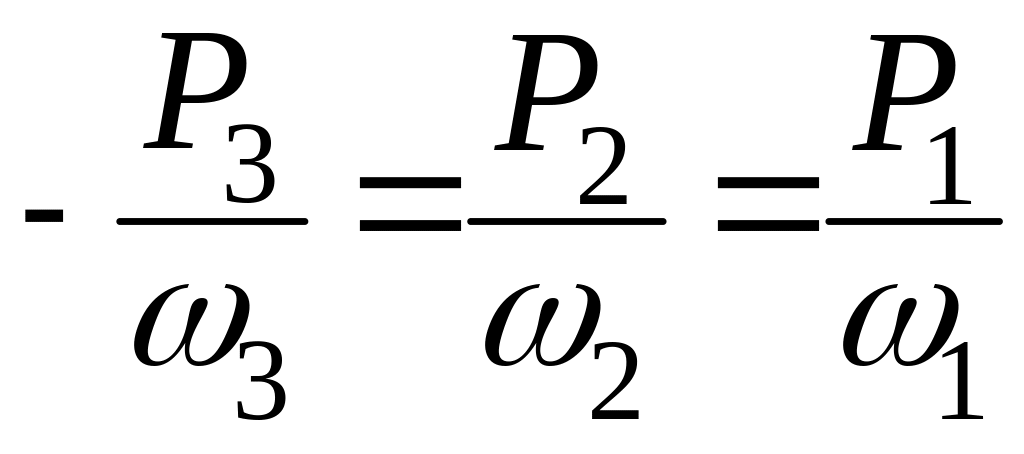 (2.91)
(2.91)
Откуда следует, что, например, при генерации субгармоники максимальная мощность, которую может получить сигнальная волна составляет
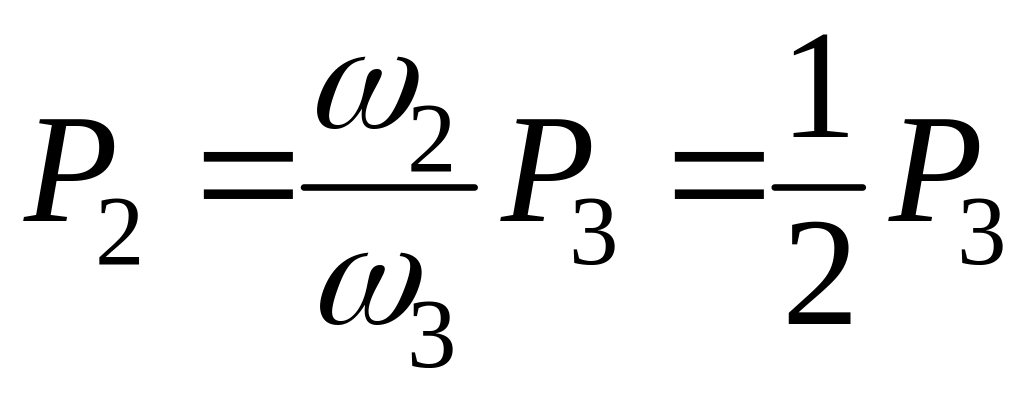 (2.92)
(2.92)
Одним из важнейших свойств параметрической генерации является возможность изменения частот и (перестройка частоты ) при фиксированной частоте накачки путем изменения дисперсионных свойств среды.
Фазовый синхронизм при трехчастотном параметрическом взаимодействии
Так
же, как и при генерации второй гармоники
(ГВГ), условия, определяемые выражениями
(2.87-2.88) для частот и волновых векторов,
могут быть выполнены в оптически
анизотропных кристаллах при взаимодействии
волн с различными поляризациями. Из
(2.87-2.88) следуют необходимые условия на
величины показателей преломления на
частотах![]() :
:
![]() .
.
В
кристаллах с нормальной дисперсией
выполнить эти условия для волн с одной
и той же поляризацией невозможно, так
как обычно
![]() .
Поэтому используются анизотропные
кристаллы, в которых величина показателя
преломления зависит не только от частоты,
но и от поляризации. Дисперсионные
зависимости показателей преломления
в таких кристаллах позволяют определить
направления синхронизма для заданной
частоты накачки.
.
Поэтому используются анизотропные
кристаллы, в которых величина показателя
преломления зависит не только от частоты,
но и от поляризации. Дисперсионные
зависимости показателей преломления
в таких кристаллах позволяют определить
направления синхронизма для заданной
частоты накачки.
Перестроечные характеристики параметрической генерации
При
заданной частоте волны накачки
в
направлении определенного синхронизма
перестройка частот
![]() может осуществляться несколькими
способами:
может осуществляться несколькими
способами:
- поворотом кристалла относительно направления угла синхронизма,
- изменением температуры кристалла,
- изменение длины волны накачки,
- использованием электрооптического эффекта (электрооптическая перестройка).
Угловая перестройка при коллинеарном параметрическом взаимодействии в одноосном кристалле
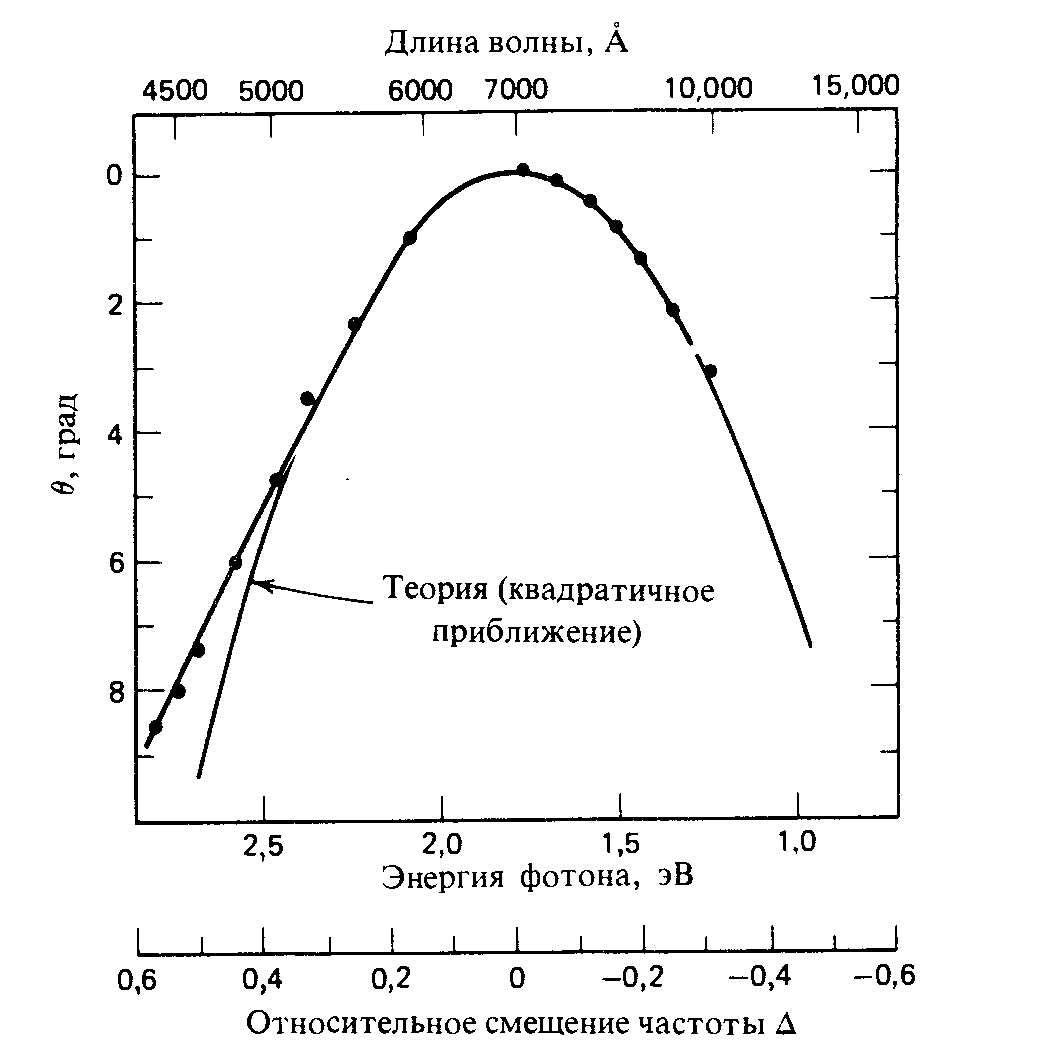
Рис. 2.44. Угловая перестроечная кривая для скалярного параметрического взаимодействия e-oo в кристалле АDP.
Температурная перестроечная характеристика параметрической генерации
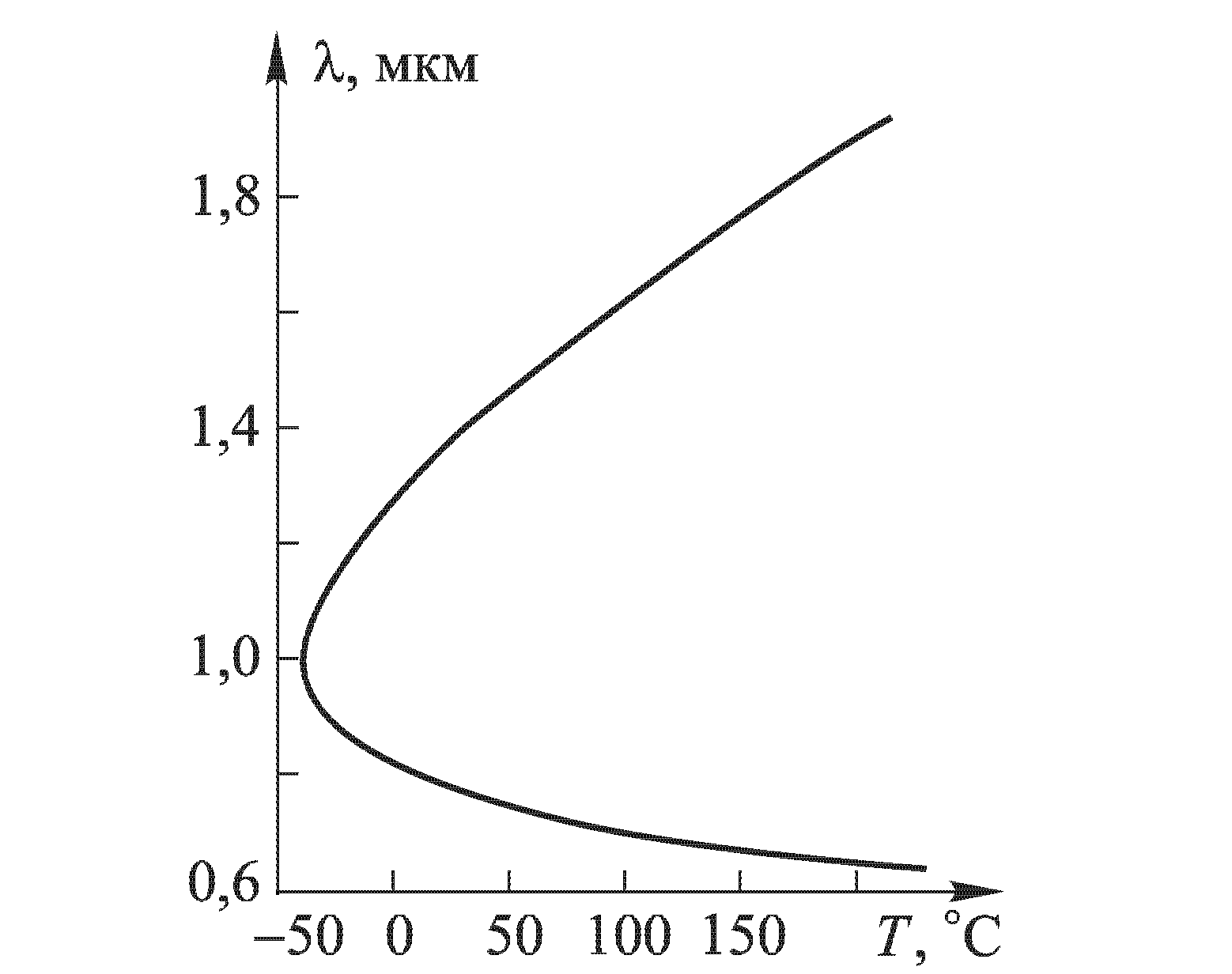
Рис. 2.46. Зависимость длин волн λ1 и λ2 параметрической генерации от температуры в кристалле BaNa-ниобата («банане») Ba2NaNb5O15 (λз =488 нм, 90о-синхронизм). Вырожденный режим реализуется при температуре около -45 С.
Перестроечная характеристика параметрической генерации при изменении длины волны накачки
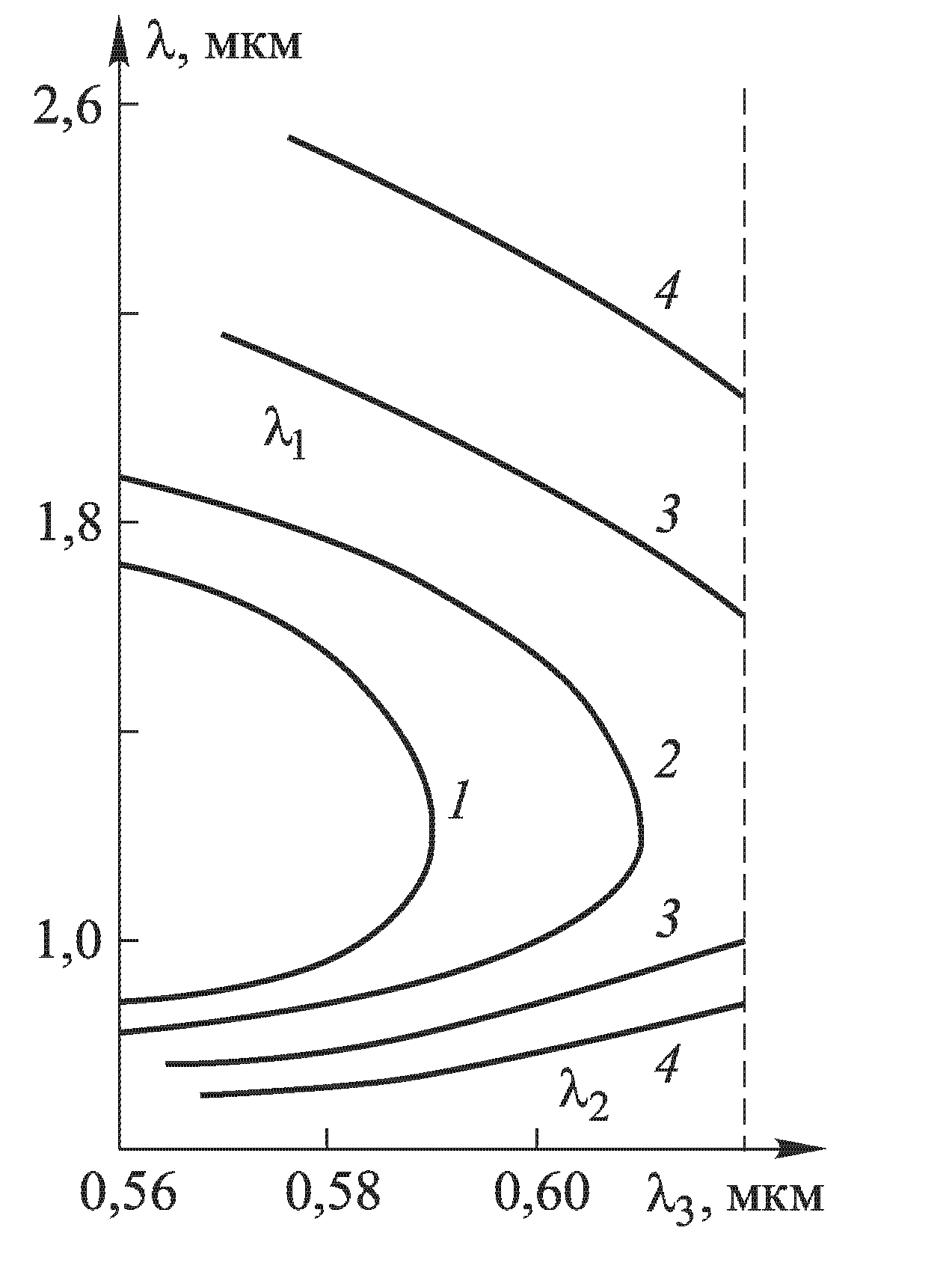
Рис. 2.47. Зависимость длин волн λ1 и λ2 параметрической генерации от длины волны накачки в кристалле LiNbO3 при 90о-синхронизме и температурах (1-225оС, 2-275оС, 3-325оС, 4-375оС).
На практике в большинстве случаев применяются угловая и температурная перестройки.
Параметрические процессы в поле сверхкоротких импульсов
Ограничимся
рассмотрением волновых пакетов с
центральными частотами
![]() :
:
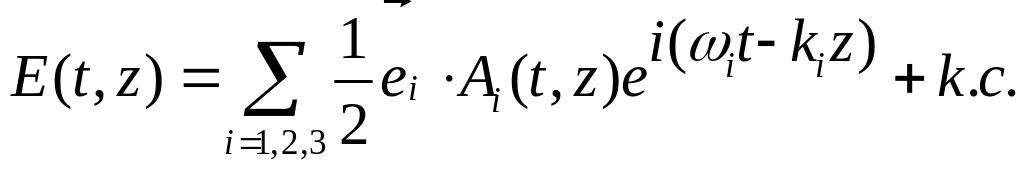 (2.104)
(2.104)
В волновое уравнение подставляем выражение (2.104). В первом приближении теории дисперсии параметрическое взаимодействие трех волновых пакетов с несущими частотами 3 (p) 1 (s)> 2 (i) представляем в виде системы из трех укороченных волновых уравнений:
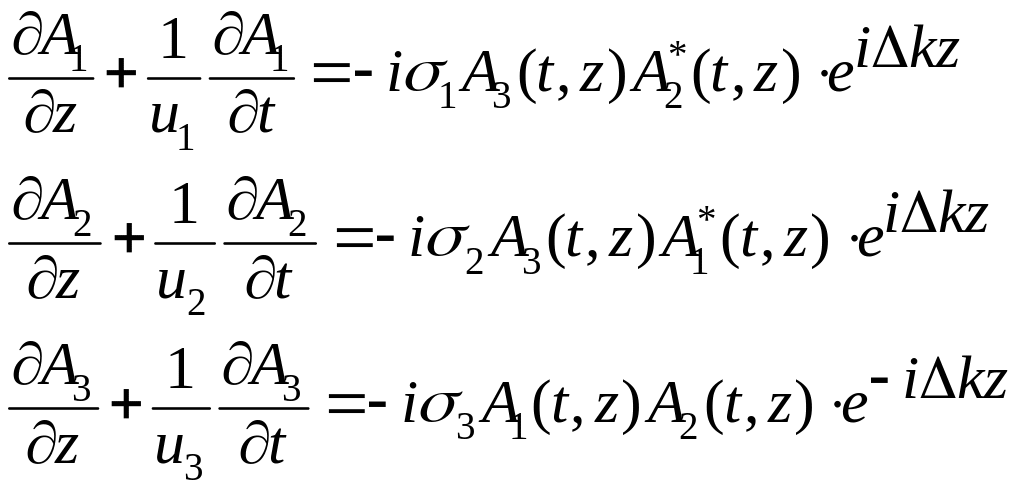 ,
(2.105)
,
(2.105)
где
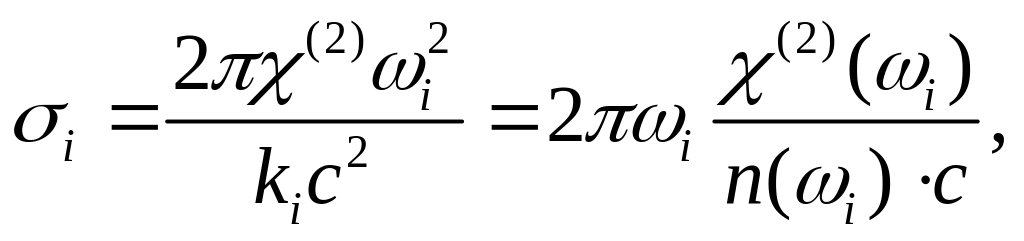 k
= k1
+
k2
k3
k
= k1
+
k2
k3
Квазистатический режим параметрического взаимодействия:
групповой и фазовый синхронизмы
В заданном поле накачки при выполнении фазового k=0 и группового u1= u2= u3 =u синхронизмов решение в бегущей системе координат =t – z/u при граничных условиях
![]() (2.106а)
(2.106а)
![]() (2.106б)
(2.106б)
![]() (2.106в)
(2.106в)
На входе в нелинейную среду кроме накачки на несущей частоте ω3 подается слабая по амплитуде волна на частоте ω1
Для
вещественных амплитуд и фаз
![]() в системе координат с =t-z/u
решение системы имеет вид
в системе координат с =t-z/u
решение системы имеет вид
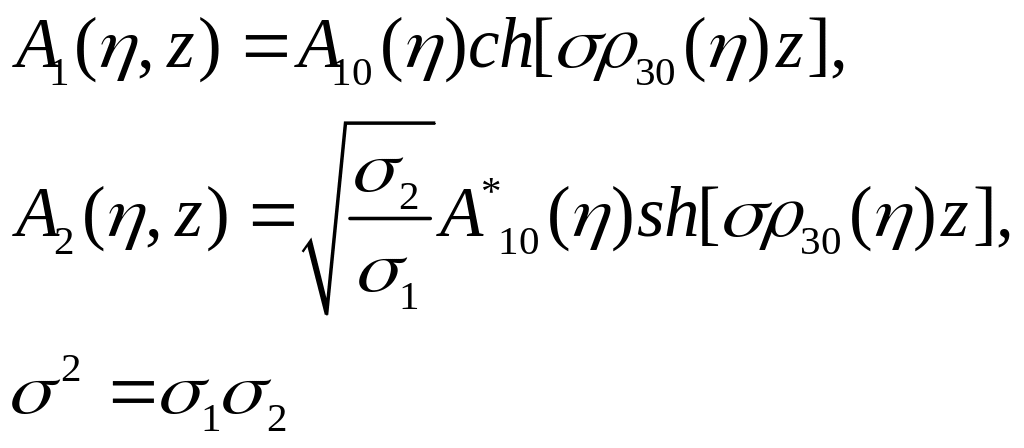 (2.107)
(2.107)
При
высоких коэффициентах усиления ch[![]() z]→
exp[
z].
z]→
exp[
z].
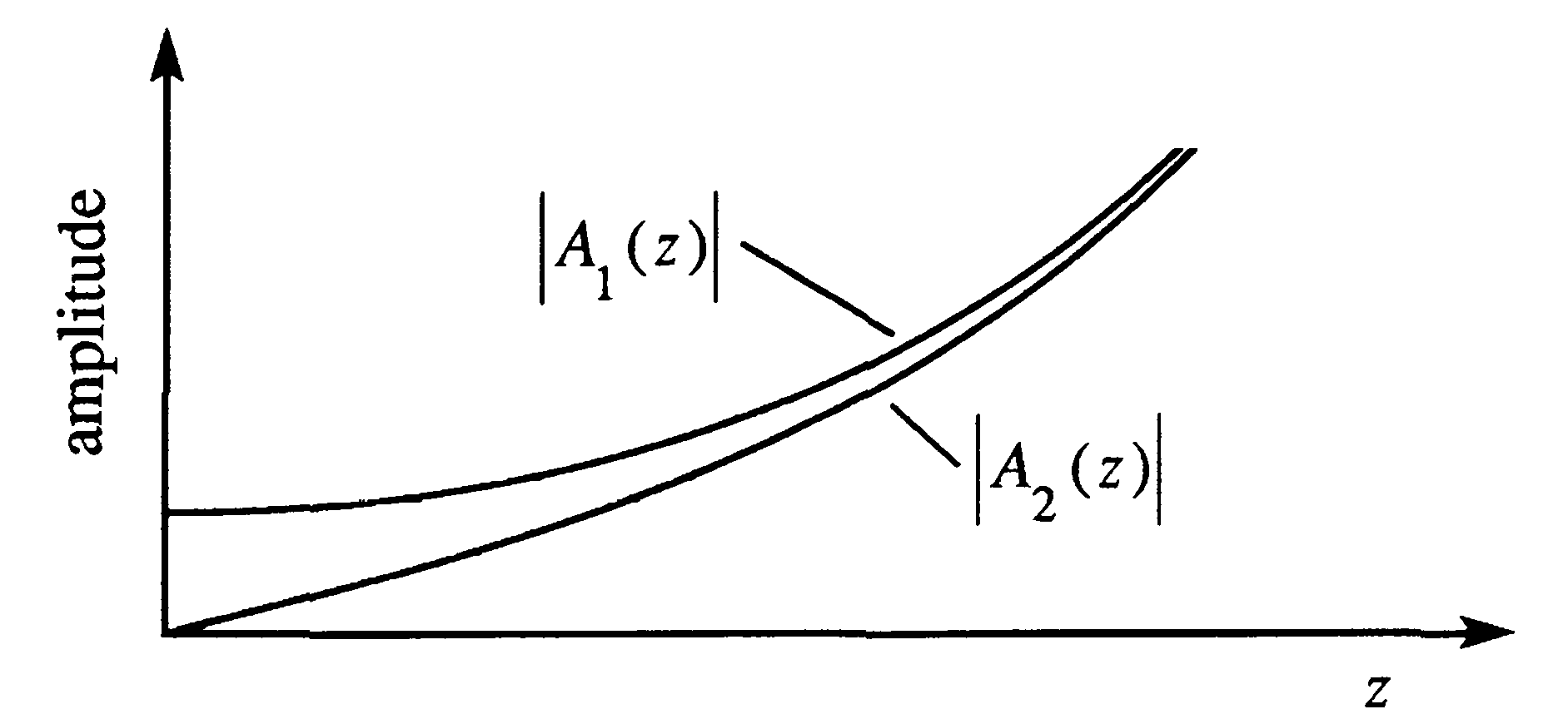
Рис.2.48. Параметрическое усиление в квазистатическом режиме параметрического взаимодействия.
При накачке спектрально ограниченным гауссовым импульсом
![]() (2.108)
(2.108)
для
амплитуды поля сигнальной волны имеем
при
![]()
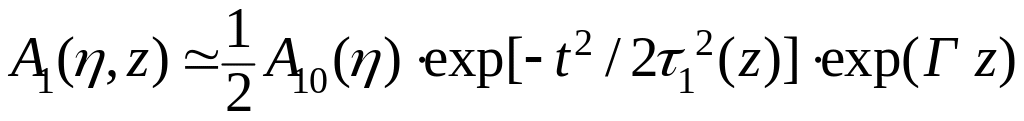 ,
(2.109)
,
(2.109)
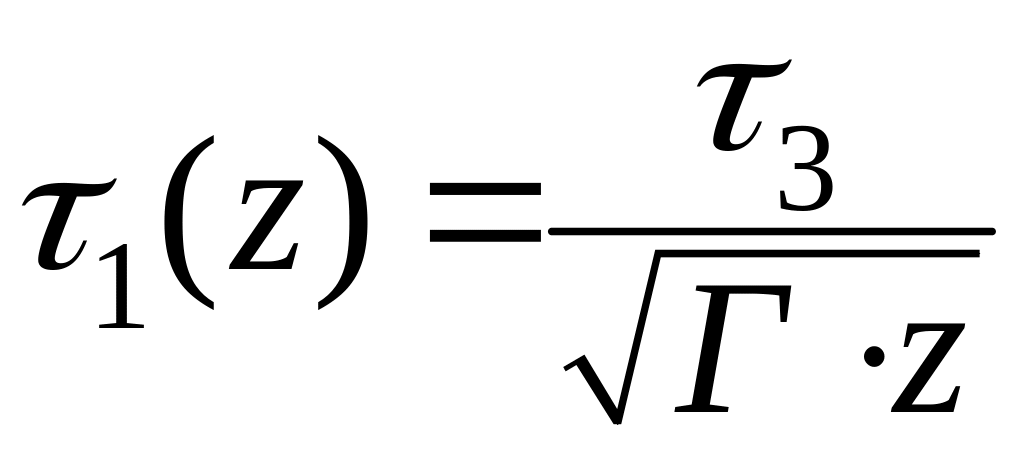 .
(2.110)
.
(2.110)
где коэффициент параметрического усиления или инкремент усиления
![]() . (2.111)
. (2.111)
Таким
образом, форма усиленного импульса
становится гауссовой при произвольной
форме импульса на сигнальной волне на
входе в нелинейную среду. При этом
длительность импульса сокращается по
закону
![]() .
.
При больших коэффициентах усиления приближение заданного поля перестает работать. С ростом коэффициента усиления амплитуда импульса на сигнальной волне достигает максимума и начинается процесс перекачки энергии в волну накачки. В результате в сигнальном импульсе возникает провал. Процесс образования провала в накачке, а затем в сигнальном импульсе показан на рис. 2.49.
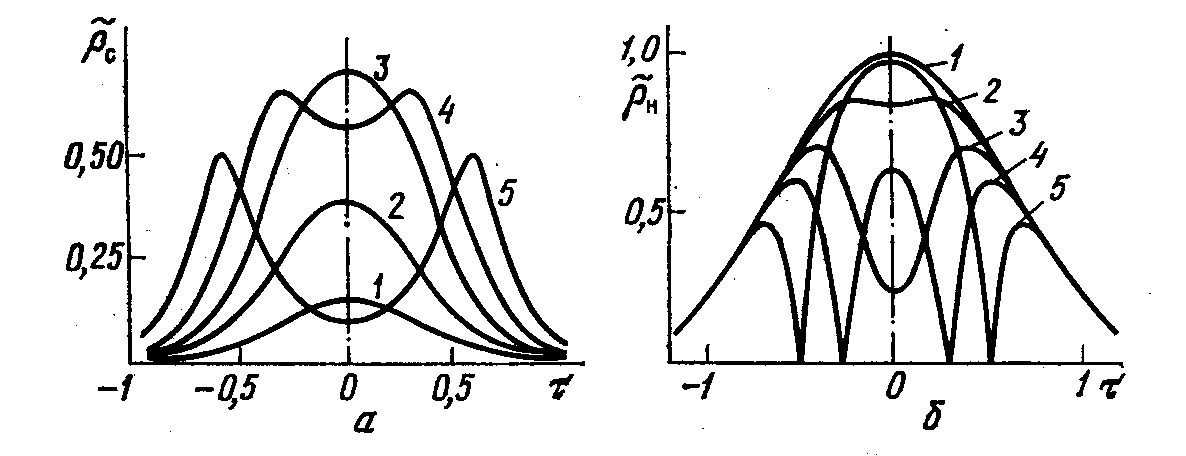
Рис. 2.49. Изменение формы сигнального импульса (а) и импульса накачки(б) при вырожденном взаимодействии в квазистатическом режиме: 1,2,3,4,5 –возрастание усиления при Гz= 5,6,7,8,10, =3 , с.н=1,3()30
Если накачка промодулирована по фазе, то фаза сигнального волны не меняется, а фазовая модуляция в накачке переносится на холостую волну
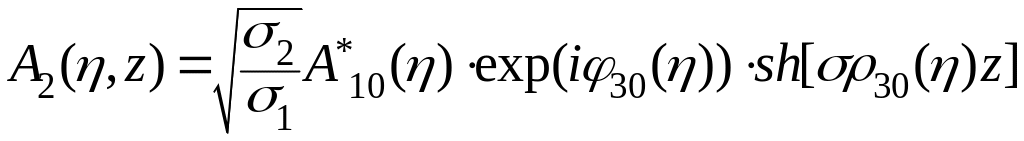 .
(2.112)
.
(2.112)
Параметр,
определяющий величину параметрического
усиления, например, на частоте сигнальной
волны,
![]() изменяется с частотой как
изменяется с частотой как
![]() .
.
Инкремент
нарастания
![]() достигает максимума при
достигает максимума при
![]() и обращается в нуль при
и обращается в нуль при
![]() и
и
![]() .
.
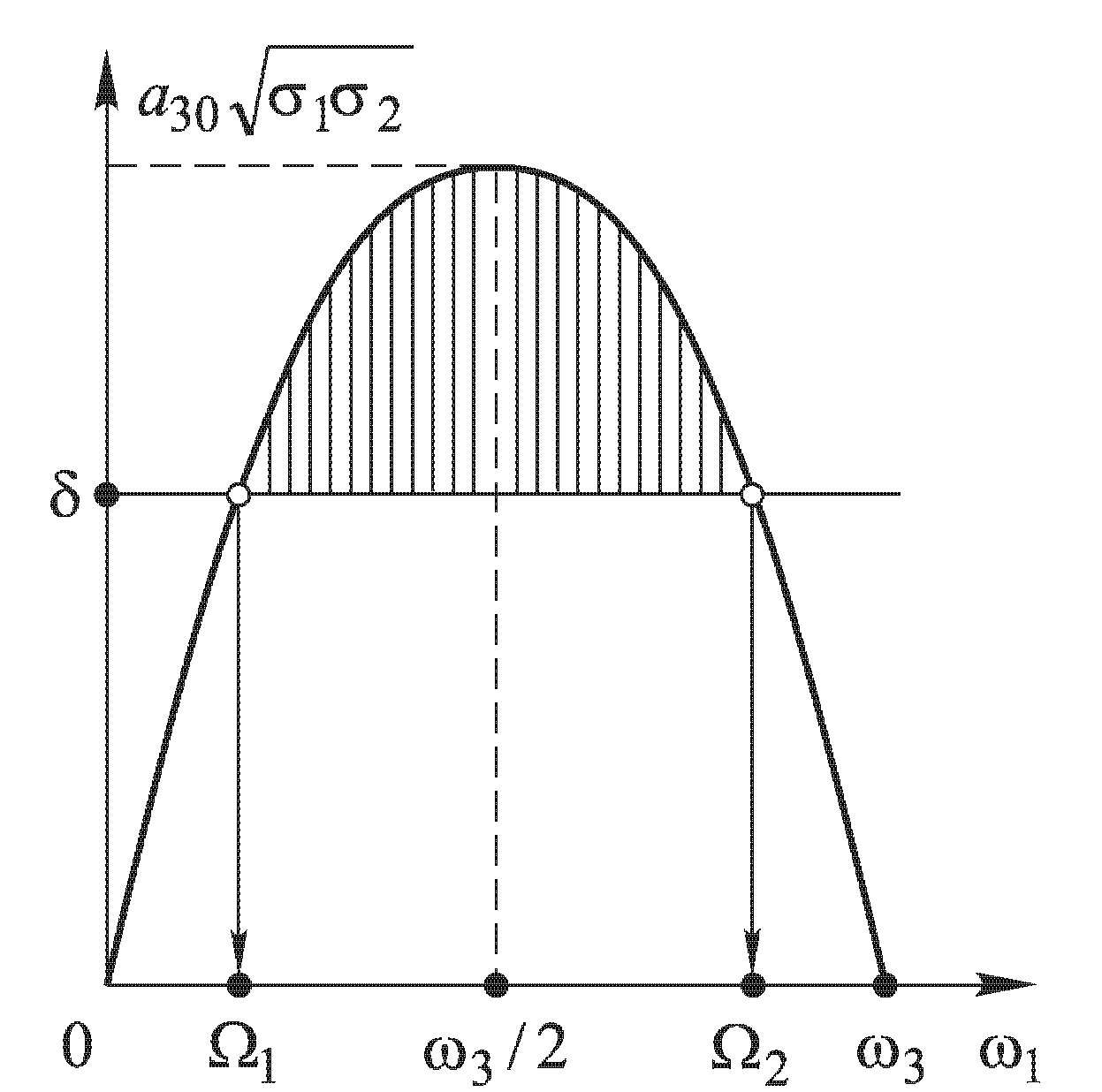
Рис.2.50. Спектральная зависимость коэффициента параметрического усиления.
Условия усиления определяются требованием превышения уровня потерь, определяемых параметром δ, для частот, удовлетворяющих неравенствам:
![]() и
и
![]() при
при
![]() ,
значение которых определяется из
,
значение которых определяется из
уравнения
![]() .
.
Нетрудно видеть, что максимальное усиление достигается в вырожденном режиме.
Как изменится инкремент нарастания, если возникнет фазовое рассогласование ∆k≠0.
В стационарном случае решение в приближении заданного поля ищется в виде
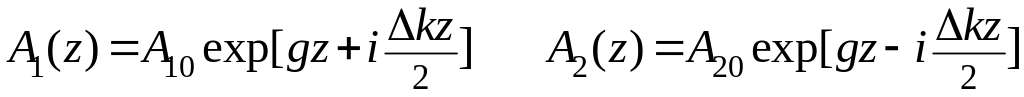 (2.113)
(2.113)
Тогда
для граничной задачи
![]() решение будет иметь вид
решение будет иметь вид
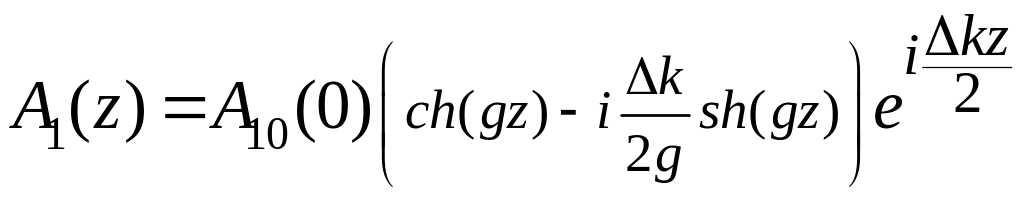 (2.114)
(2.114)
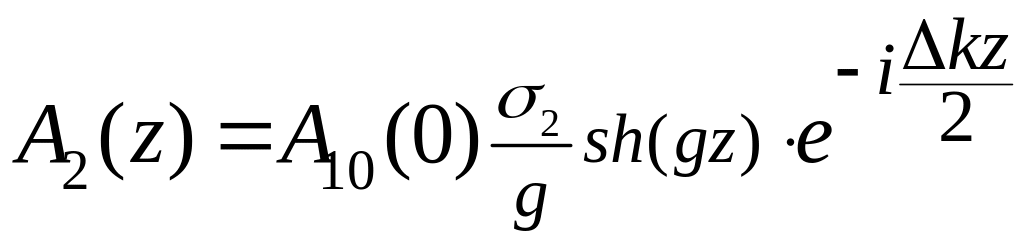 (2.115)
(2.115)
эффективный
инкремент усиления
![]() будет определяться выражением
будет определяться выражением
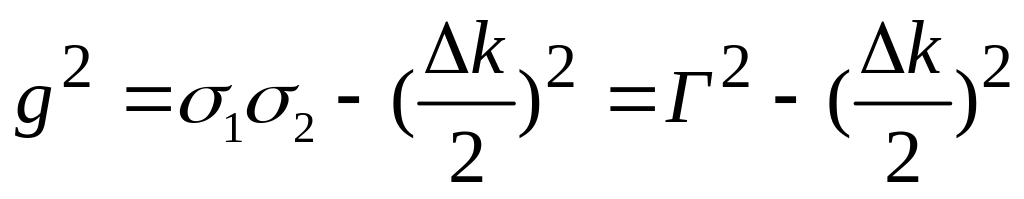 (2.116)
(2.116)
Нестационарный режим параметрического взаимодействия при k=0, но u1 ~ u2 ≠ u3
Групповая расстройка сигнальной и холостой волн с накачкой
Пусть групповые скорости сигнального и холостого импульсов равны или близки по величине, а их групповая расстройка по отношению к импульсу накачки велика, т.е.
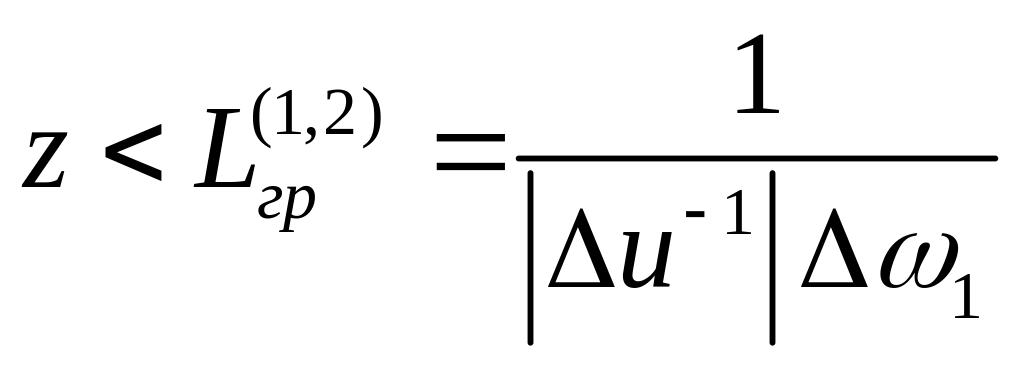 ,
но
,
но
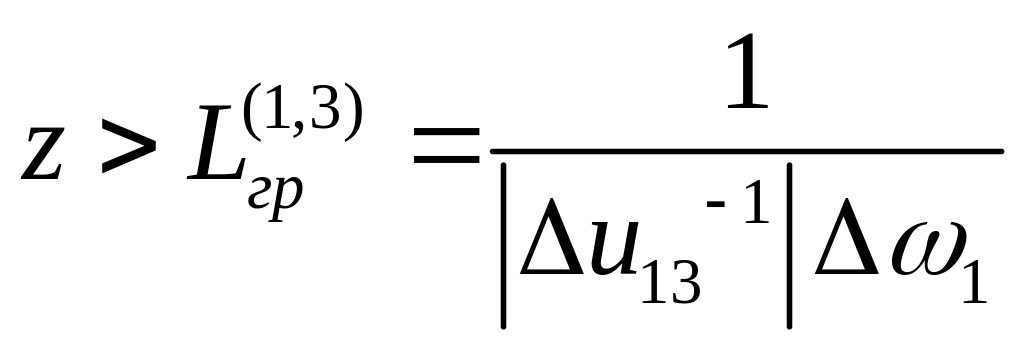 и
и
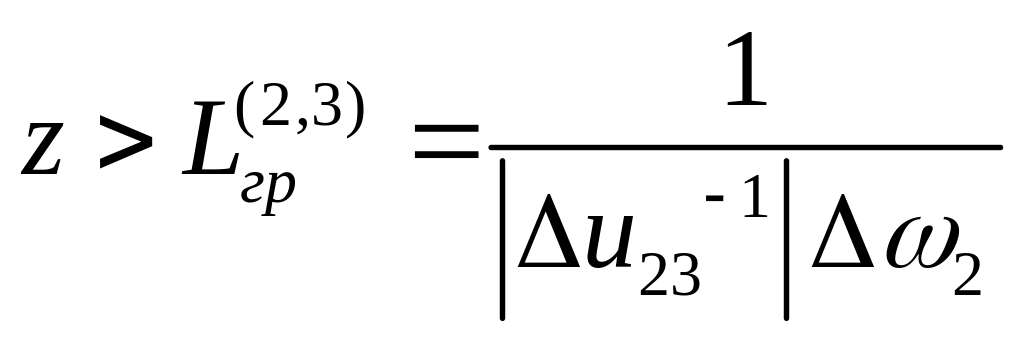 ,
(2.117)
,
(2.117)
где Lгр- длина групповой расстройки
Тогда в приближении заданного поля накачки для сигнального импульса решение имеет вид
![]() ,
(2.118)
,
(2.118)
где
![]() =t-z/u1,
=t-z/u1,
![]() =u1-1-u3-1.
=u1-1-u3-1.
Расстройка снижает усиление. В зависимости от соотношения между групповыми скоростями u1 и u3 преимущественно усиливается или фронт (u1<uн), или хвост (u1>uн) сигнального импульса, при этом происходит его уширение.

Рис. 2.51.
