Середнє квадратичне відхилення знаходимо за такою формулою:
,
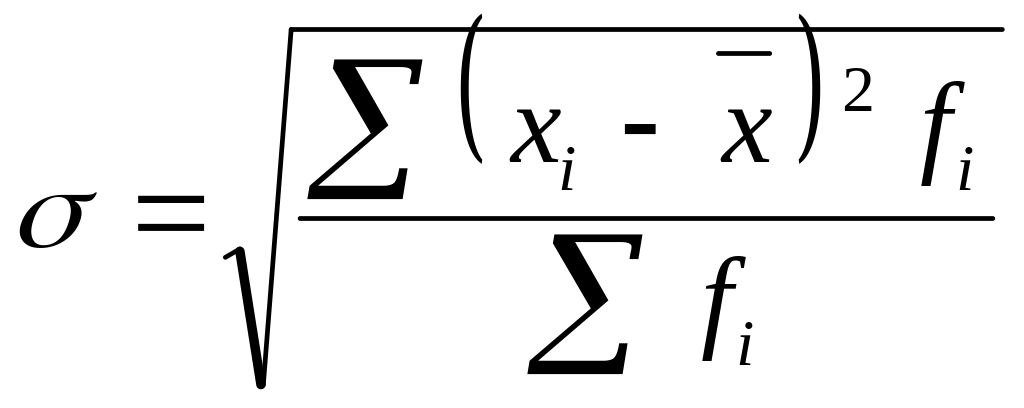де
хі – індивідуальні значення окремої ознаки, варіанти
– середня арифметична (середнє значення ознаки)
fi – частота відповідної ознаки.
Для розрахунку використовуємо дані все ж з тієї таблиці 3.1
=
√ ((2,75-5,6)2
*29329354))+((7,05-5,6)2
*12498802))+
((11,35-5,6)2 *5674404))+((15,65-5,6)2 *3458367)))/50960927=
√ (238154354,48+26247484,20+187595796,24+349295067,00)/ 50960927
=√(801292701,92/ 50960927)= √15,72=3,96 тис.грн. /ос .
Для знаходження дисперсії використовуємо таку формулу:
,
де
хі – індивідуальні значення окремої ознаки, варіанти
– середня арифметична (середнє значення ознаки)
fi – частота відповідної ознаки.
2 = ((2,75-5,6)2 *29329354))+((7,05-5,6)2 *12498802))+
((11,35-5,6)2 *5674404))+((15,65-5,6)2 *3458367)))/50960927=
(238154354,48+26247484,20+187595796,24+349295067,00)/ 50960927
=(801292701,92/ 50960927)= 15,72 тис.грн. /ос .
Лінійний коефіцієнт варіації:
·100
%
=
(3,96
/5,6)
* 100% = 70,71%
5. Квадратичний коефіцієнт варіації:
·100
%
V = (4,01/ 5,6)* 100% =71,61%
Таблиця 4.2
Обсяг дебіторської заборгованості на душу населення, тис.грн. /ос |
Кількість населення, ос. |
Дискрет ний ряд |
Середня арифметична зважена х=∑xi*fi/∑ fi |
│xi - │ тис.грн. /ос. |
│xi - │fi тис.грн. /ос.
|
(xi - )2 тис.грн. /ос. |
(xi - )2fi тис.грн. /ос. |
( fi ) |
(xi) |
||||||
Від 0,6 до 4,9 |
29329354 |
2,75 |
5,6 |
2,85 |
83588658,90 |
8,12 |
238154354,48 |
Від 4,9 до 9,2 |
12498802 |
7,05 |
1,45 |
23622735,78 |
2,10 |
26247484,20 |
|
Від 9,2 до 13,5 |
5674404 |
11,35 |
5,75 |
32627823,00 |
33,06 |
187595796,24 |
|
Від 13,5 до 17,8 |
3458367 |
15,65 |
10,05 |
34756588,35 |
101,00 |
349295067,00 |
|
Разом |
50960927 |
Х |
|
Х |
174595806,03 |
Х |
801292701,92 |
Висновки:
Критерієм
однорідності сукупності найчастіше
виступає квадратичний коефіцієнт
варіації (
),
який визначається відношенням середнього
відхилення до середньої арифметичної
величини. Чим менше середнє відхилення,
тим більш типова середня, тим більш
однорідна сукупність. Так
як
V
> 33% (V
= 71,61%)– високий рівень варіації, сукупність
неоднорідна, значення середньої (
= 5,6)
неможна вважати типовим рівнем ознаки
в даній сукупності.
Завдання 4.
Використовуючи результати розрахунків завдання 3 даної теми утворюємо робочу таблицю 4.3, в якій будуємо графи для розрахунку коефіцієнтів асиметрії (A) та ексцесу (E). Обчислюємо дані показники: