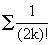4) Тестирование

Для тестирования выбираются такие уравнения, у которых корень можно найти аналитически. Значения a  и b выбираются таким образом, чтобы [a,b] содержал искомый корень и притом только один.

№ теста	f(x)	a	b	Прогнозируемый результат	Полученный результат
1	x3 - 1	0	1.5	1	0.9999
2	x2 + 2x	-2.5	-1	-2	-1.9999
3	ex - 1	-0.5	1	0	0.0001

Ручная  трассировка:

исходные данные f(x)= х³ + 0,5 x² - 2, a=0, b=2, E=0.1

c=(a+b)/2	f(a)*f(c)	a	b	b-a	b-a<e
(0+2)/2=1	f(0)*f(1)>0	1	2	1	false
(1+2)/2=1.5	f(1)*f(1.5)<0	1	1.5	0.5	false
(1+1.5)/2=1.25	f(1)*f(1.25)>0	1.25	1.5	0.25	false
(1.25+1.5)/2=1.38	f(1.25)*f(1.38)>0	1.38	1.5	0.12	false
(1.38+1.5)/2=1.44	f(1.38)*f(1.44)>0	1.44	1.5	0.06	true

x=(1.44+1.5)/2= 1.47

Пример 2.

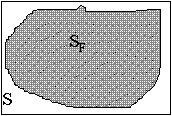
Найти площадь заштрихованной фигуры методом Монте- Карло. Вычисление площади оформить как процедуру, в основной программе вводится число точек и выводится результат.

1) постановка задачи

Дано: фигура, ограниченная y=x²  и y=2

Надо: найти площадь фигуры.

2) математическая модель

Метод Монте-Карло позволяет находить приближенно площадь произвольной фигуры.

Для этого фигура помещается внутрь прямоугольника или квадрата, площадь которого известна и равна S. Прямоугольник (квадрат) случайным образом заполняется N точками. Если внутрь фигуры F попали М точек, то отношение M/N приближенно равно отношению площадей SF/S.

= , отсюда S_F =S*M/N.

В данном примере фигура, площадь которой необходимо найти, ограничена линией y=x² и помещена в прямоугольник ABCD. AB=1, AD=2.

Для решения задачи необходимо задать: N - общее число точек, S - площадь прямоугольника, содержащего фигуру, x,y - координаты точки, выбранные случайным образом внутри прямоугольника (-1<x<1, 0<y<1).

Чтобы подсчитать количество точек (x,y), принадлежащих фигуре (переменная  M), необходимо проверить условие y>x².

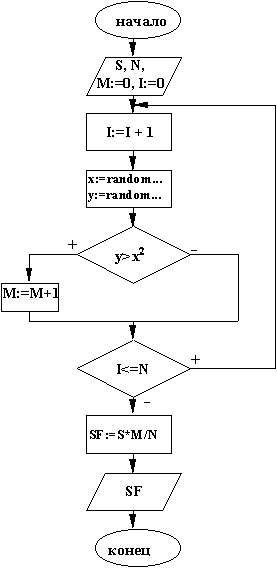
3) блок-схема

4) программа Program Pr2;   Var        S, SF: real;        M,N: integer; Procedure MonteKarlo(N: integer; S: real; Var SF:real);     Var           M, I: integer;           X,Y: real;      Begin         M:=0;         For i:=1 to n do               Begin                  X:=Random(20)/10-1;                  Y:=Random(10)/10;                  If   y<x*x   then  M:=M+1;               End;         SF:=S*M/N; End; BEGIN    {основная программа}     randomize;     Write('N='); Readln(n); S:=2;      MonteKarlo(N, S, SF);      writeln('SF=', SF:6:3); END.

Результат выполнения программы: при N=100    SF=1.226

5) тестирование

Для тестирования можно изменить исходные данные, например, общее количество точек N и размеры прямоугольника, содержащего фигуру.

№ теста	N	S	X	Y	SF
1	1000	4	[-2,2]	[0,1]	1.204
2	1000	4	[-1,1]	[-1,1]	1.212

 

Пример 3.

Найти значение суммы + + + ... с точностью E=0.00001 и определить количество слагаемых этой суммы.

1) постановка задачи

Найти сумму с заданной точностью - это значит выполнять вычисления, добавляя к сумме по одному слагаемому, до тех пор, пока разница между предыдущим и последующим значением суммы не станет меньше точности Е.

Дано:

Найти: S, n такие, что

-

< E

2) математическая модель

-

=

< E - условие прекращения суммирования

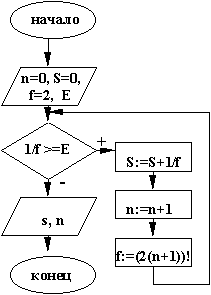
3) блок-схема n- номер очередного слагаемого,    E - точность,   f - факториал  знаменателя,   S -сумма

4) программа Program Pr3;    Procedure Fakt(k: integer; Var f: integer);        Var i: integer;         Begin               f:=1;               For i:=1 to k do f:=f*i;         End; Var    S, E:  real;          n, f: integer; BEGIN {основная программа}       S:=0;  n:=0;  f:=2;  E:=0.00001;       while 1/f>=E do           begin                S:=S+1/f;   n:=n+1;   Fakt(2*(n+1),f);           end;       writeln(‘S=‘,s:8:5,’n=‘,n) END.

Результат выполнения программы: S= 0.54308 n=4

5) тестирование

Для тестирования вычислим вручную значение суммы и количество слагаемых для различных значений Е.

№ теста	Проверяемый случай	Прогнозируемый результат		Полученный результат
		S	N	S	N
1	Е=0.1	0.5	1	0.5	1
2	Е=0.01	0.54167	2	0.54167	2

1) Е=0.1                                              

1/2! = 1/2 = 0.5 >0.1 -суммируем          n=1                

1/4!= 1/24=0.04167 < 0.1 - завершаем суммирование                           

Результат :    S = 0.5    n=1                                                 

2) E=0.01

1/2! = 1/2 = 0.5 >0.01 -    суммируем           n=1

1/4!= 1/24=0.04167 > 0.01 - суммируем       n=2

1/6!= 1/720 =0.00139< 0.001- завершаем суммирование 

Результат : S=0.54167  n=2

Пример 4.

Вычислить значение многочлена p(x)=3,4х⁵ - 2х⁴ +5,7х³ -0,4х+3 при х=15,35 по схеме Горнера.

1) математическая  модель

Преобразуем многочлен a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2... + a₁x + a_0, группируя его члены и вынося за скобки х:

a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 +... +а₂х² + a₁x + a₀ = (a_nx^n-1 + a_n-1x^n-2 + a_n-2x^n-3 +... +а₂х + a₁)x + a₀ = ((a_nx^n-2 + a_n-1x^n-3 + a_n-2x^n-4 +... +а₂)х + a₁)x + a₀ = …

Действуя таким образом, приведем многочлен к виду:

((...(a_nx + a_n-1)x + a_n-2)x +...)x +a₁)x +a_0. Тогда последовательно находятся:

p= a_n

p= a_nx + a_n-1

p=(a_nx + a_n-1)x + a_n-2

_{...................................................}

p= _(...(a_nx + a_n-1)x + a_n-2)x +...)x +a₁)x +a₀

Каждое следующее значение получается из предыдущего домножением на х и прибавлением очередного коэффициента многочлена:

p=p*x + a_k

2) программа

Program Pr4;

   Сonst

          n=5;

   Type

          mas=array[1..100] of real;

   Var

       a: mas;   p, x: real;     k: integer;

  Procedure Gorner(x: real; a: mas; Var p: real);

      Var

           i: integer;

     Begin

          p:=a[n];    For i:=n-1 downto 0 do

                                p:=p*x+a[i];

     End;

BEGIN     {основная   программа}

      Writeln('Введите коэффициенты'); For k:=0 to n do Readln(a[k]);

      Write('Введите x '); Readln(x); Gorner(x,a,p);

      Writeln('p=',p:6:3);

END.

Результат выполнения программы: 

р=2807059.189

3) тестирование

№ теста	Проверяемый случай	Прогнозируемый результат	Полученный результат
1	х=0	р(0)=3	р(0)=3
2	х=1	р(1)=9.7	р(1)=9.7
3	х=-1	р(-1)=-7.7	р(-1)=-7.7

П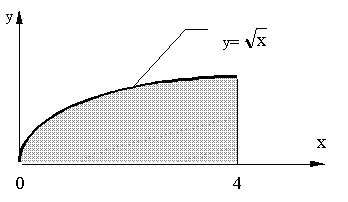 ример 5.

Найти площадь криволинейной трапеции, ограниченной линиями:

y=f(x),  x=a,  x=b, если

f(x) = , a=0,  b=4.

 

1) математическая модель

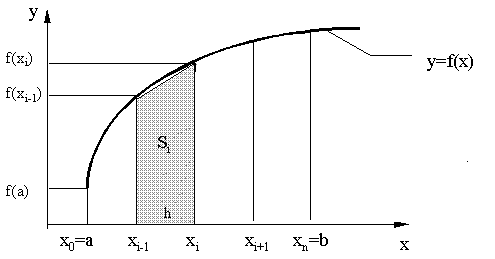
Можно найти приближенное значение площади криволинейной трапеции, ограниченной линиями y=f(x), x=a, x=b, используя метод трапеций. Для этого разобьем отрезок [a, b] на n равных частей и через точки разбиения проведем вертикальные прямые до пересечения с графиком функции y=f(x). Соединив точки пересечения отрезками, получим n прямоугольных трапеций с высотой h= .

Тогда S_ABCD = , где S_i = . Чем больше n, тем точнее результат вычисления.  =h ( + + + + +...+ + ) =

= h( +f(x₁) +f(x₂)+...+ f(x_n-1) + )

2) программа

Program Pr5;

    Function F(x: real): real;

      Begin

            F:=sqrt(x);

     End;

   Var

       a, b, h, x, s: real;    n: integer;

BEGIN  {основная  программа}

      write('a, b = '); Readln(a, b); write('n = '); Readln(n);

      h:=(b-a)/n; s:=(f(a)+f(b))/2;   x:=a+h;

      while x<b do

          begin

               s:=s+f(x); x:=x+h;

         end;

      writeln('s=', s*h:8:4);

END.

3) тестирование

Исходные данные следует подобрать таким образом, чтобы площадь криволинейной трапеции можно было вычислить аналитически (площадь криволинейной трапеции  равна значению определенного интеграла)

№ теста	Проверяемый случай			Прогнозируемый результат	Полученный результат
	f(x)	a	b
1	x2	0	1	0,33	0,3333
2	ex	-1	1	2,35	2,3504