Сопротивление материалов (Бормотов А) / Ответы на вопросы к экзамену Сопромат

Ответы на вопросы к экзамену БЖД

29. Где справедлива гипотеза плоских сечений? Принцип Сен-Венана - Принцип Сен-Венана - если совокупность некоторых сил, приложенных к небольшой части поверхности тела, заменить статически эквивалентной системой других сил, то такая замена не вызовет существенных изменений в условиях нагружения частей тела, достаточно удаленных от мест приложения исходной системы сил. Гипотеза справедлива лишь на некотором удалении от места приложения внешней нагрузки и места резкого изменения поперечного сечения бруса.

30. Вывести формулы для перемещений при центральном растяжении-сжатии. - 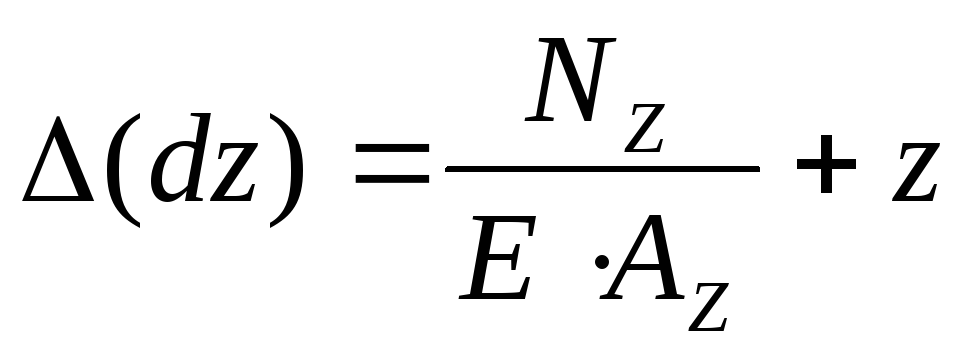- удлинение (укорочение) элемента бруса, длиной dz.

; при z₁=0 и z₂=z, то - перемещение сечения z вдоль оси бруса.

29. Вывести формулу для определения потенциальной энергии при центральном растяжении-сжатии. - 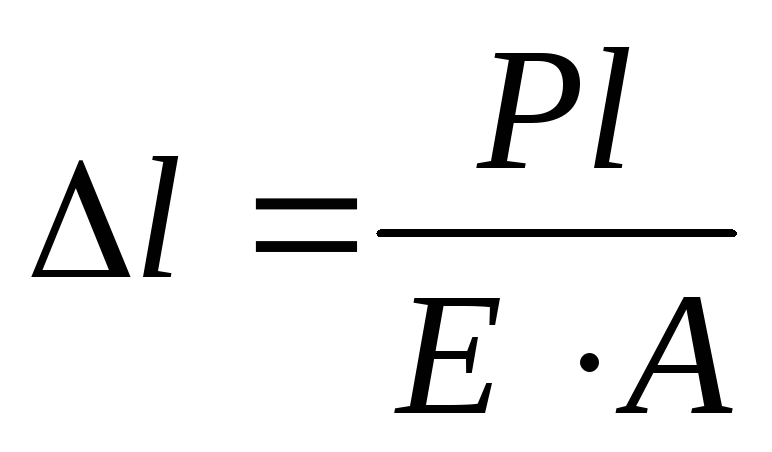- удлинение бруса. На элементарном перемещении работа тянущей силы равна: dT = Pd()=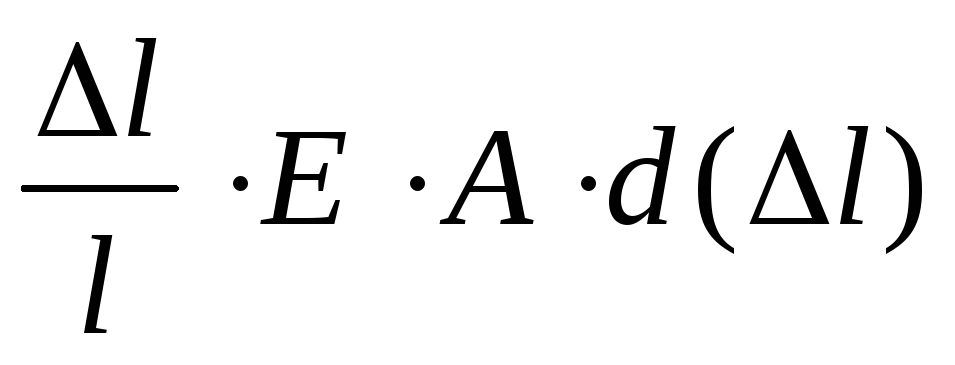. Отсюда:

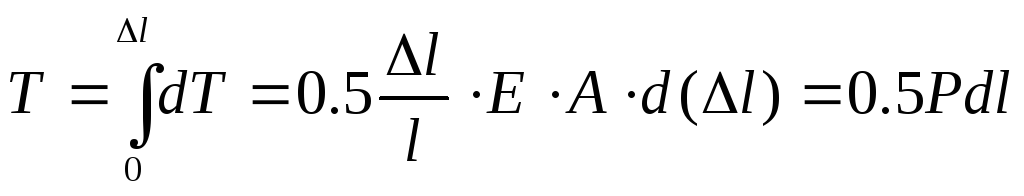
T=U, значит U=0.5Pdl. С учетом :

29. Вывести формулы для напряжений в наклонных сечениях бруса при центральном растяжении-сжатии. Где действуют наибольшие нормальные и касательные напряжения и чему они равны? –

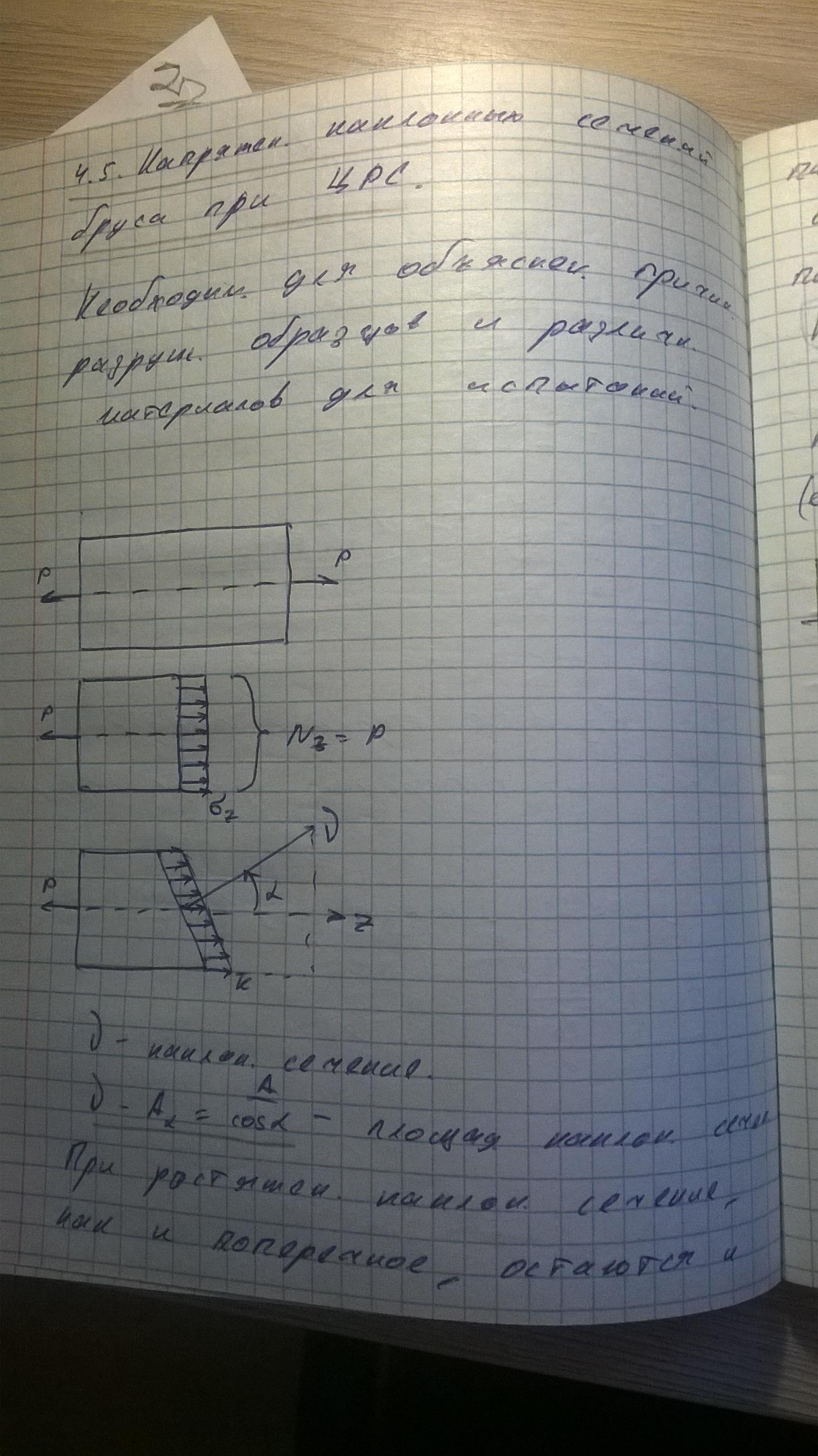
29. Вывести формулы для напряжений в наклонном сечении бруса при двухосном растяжении-сжатии. Пример получения чистого сдвига. –

29. Вывести закон Гука при двухосном и трехосном растяжении-сжатии. –

29. Вывести формулу изменения объема при трехосном растяжении-сжатии. Установить пределы изменения коэффициента Пуассона. –

29. Удельная потенциальная энергия при трехосном растяжении-сжатии. –

29. Машинная диаграмма при испытании образца на растяжение. Ее основные зоны. Объяснить происхождение линий сдвига (линии Чернова) на поверхности плоского образца. –

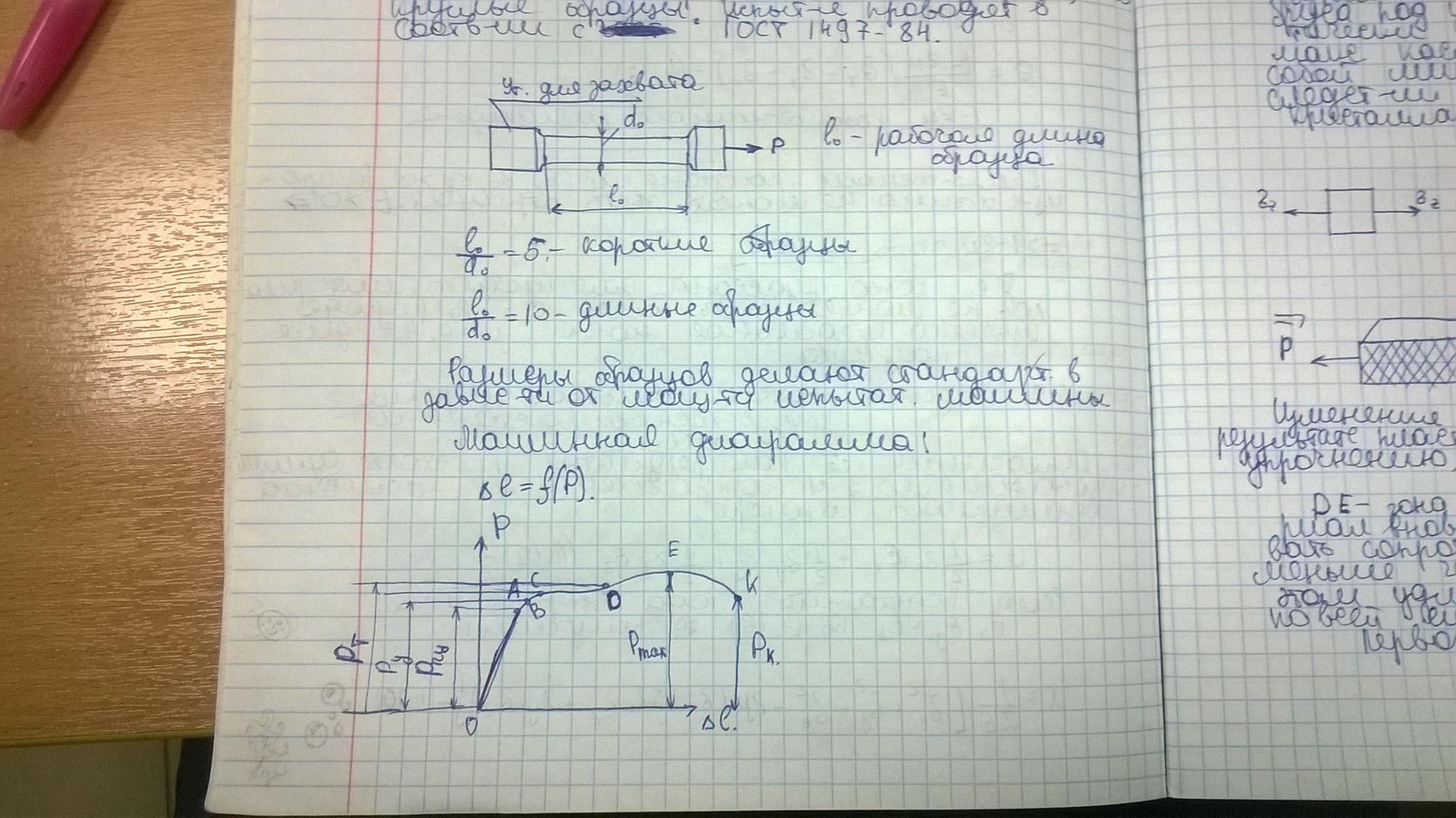
29. Диаграмма условных и истинных напряжений. Основные прочностные характеристики материала. - Предел пропорциональности, Предел упругости, Предел текучести, Предел прочности (временное сопротивление).

30. Что такое условный предел текучести материала? – напряжение, соответствующее остаточной деформации ε_Т

31. Характеристики пластичности материала. - 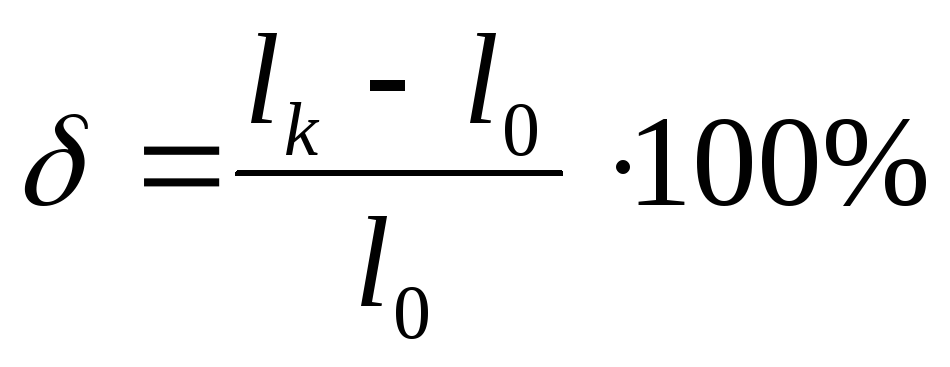- относительное удлинение образца при разрыве.

- относительное уменьшение площади сечения образца в месте разрыва. , - до нагружения; , - после разрыва образца; - площадь сечения шейки разорванного образца

29. Закон разгрузки и повторного нагружения. Наклеп. – (нагартовка) – явление повышения упругих свойств материала в результате предварительной пластичной деформации. Применяется для упрочнения поверхностного слоя деталей.

30. Какие материалы (пластичные, хрупкие) проявляют большее сопротивление отрыву частиц, чем сдвигу их друг относительно друга и как они разрушаются при кручении образца. Почему? – Пластичные материалы проявляют большее сопротивление отрыву частиц, чем сдвигу их друг относительно друга и разрушается главным образом от сдвига частиц в плоскостях действия наибольшего касательного напряжения τ_max (б).

31. Что такое предельные напряжения? – напряжения, при которых появляется пластичная деформация (если материал пластичный) или признаки хрупкого разрушения, если материал хрупкий. σ_пред=σ_Т; σ_пред=σ_пч

32. Дать определение предела текучести, предела пропорциональности, предела упругости, временного сопротивления. Показать их на диаграмме – Предел текучести – напряжение, при котором деформация растет без заметного увеличения нагрузки 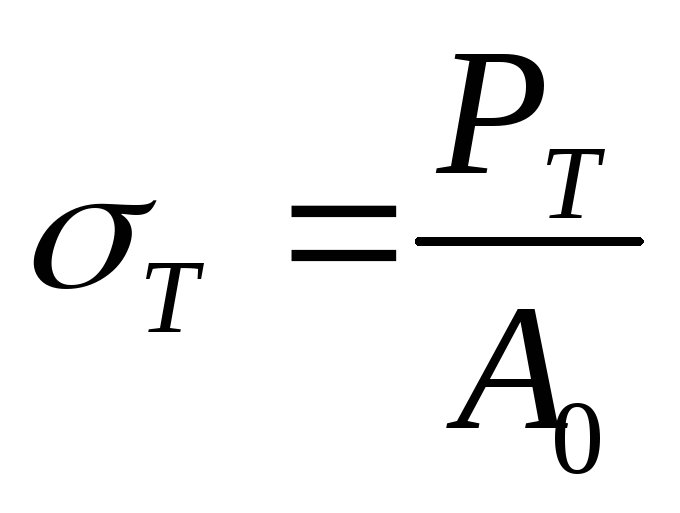; Предел пропорциональности – значение напряжения, превышение которого приводит к отклонению от закона Гука. 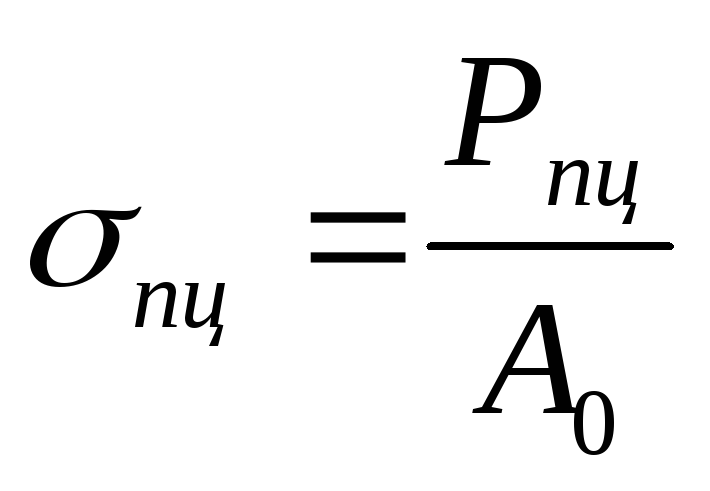[Па]; Предел упругости – наибольшее напряжение, до которого материал не получает остаточного напряжения. 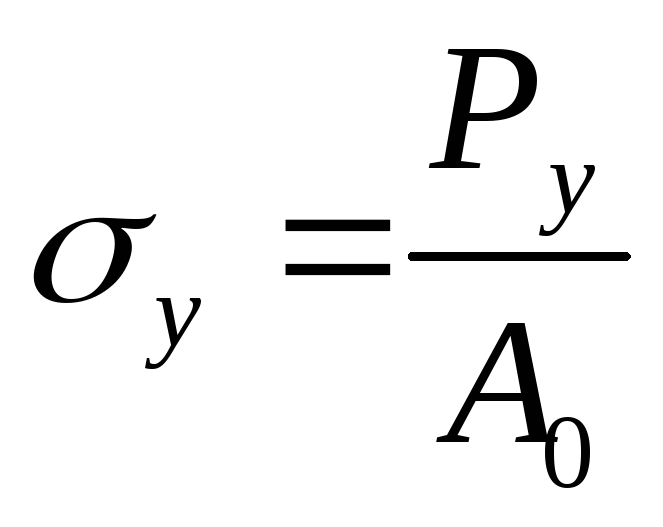; Предел прочности (временное сопротивление) – максимальное напряжение, выдерживаемое материалом при растяжении.

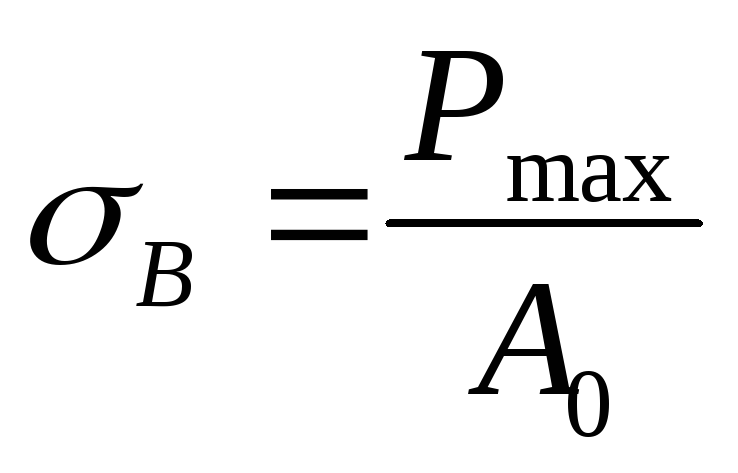
33. Что такое допускаемые напряжения? – наибольшие напряжения, при которых обеспечивается прочность и долговечность конструкции.

34. Чистый сдвиг. Примеры его получения. Установить связь между упругими постоянными материала Е, m, G для изотропного материала. – напряженно-деформируемое состояние, характеризующееся тем, что на гранях элемента действительно касательное напряжение. Пример получения: кручение трубчатых образцов. Связь между упругими постоянными, проверенное экспериментально:

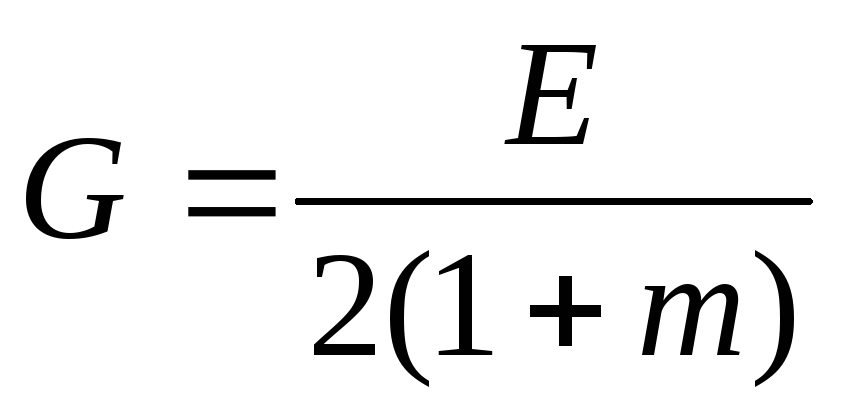
35. Выражение удельной потенциальной энергии при сдвиге. - 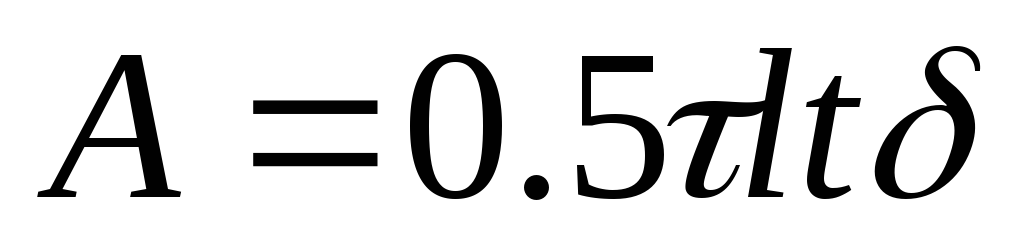- работа касательных сил;

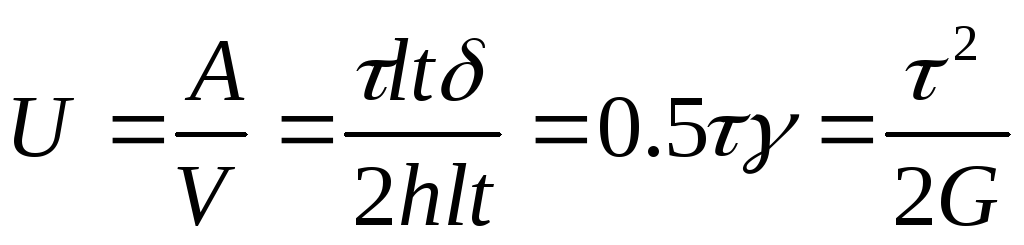
36. Вывести формулы для определения напряжений и деформаций при кручении бруса круглого сечения (геометрическое, физическое, статическое, синтезирующее уравнения). -

37. Потенциальная энергия при кручении бруса. - 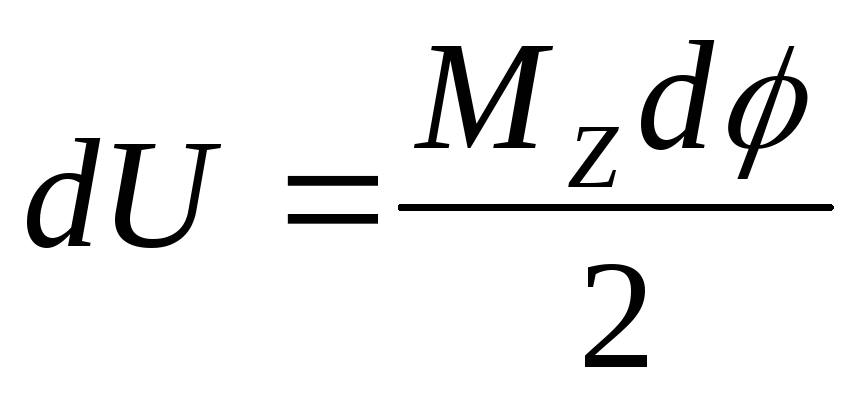- энергия, накопленная в элементе бруса, длиной dz.

- угол поворота одного сечения по отношению к др удаленному от него на р-ние z; - жесткость бруса при кручении. Тогда: - энергия, накопленная в брусе, длиной l.

29. Объяснить характер разрушения бруса круглого сечения из хрупкого и пластичного материала. –

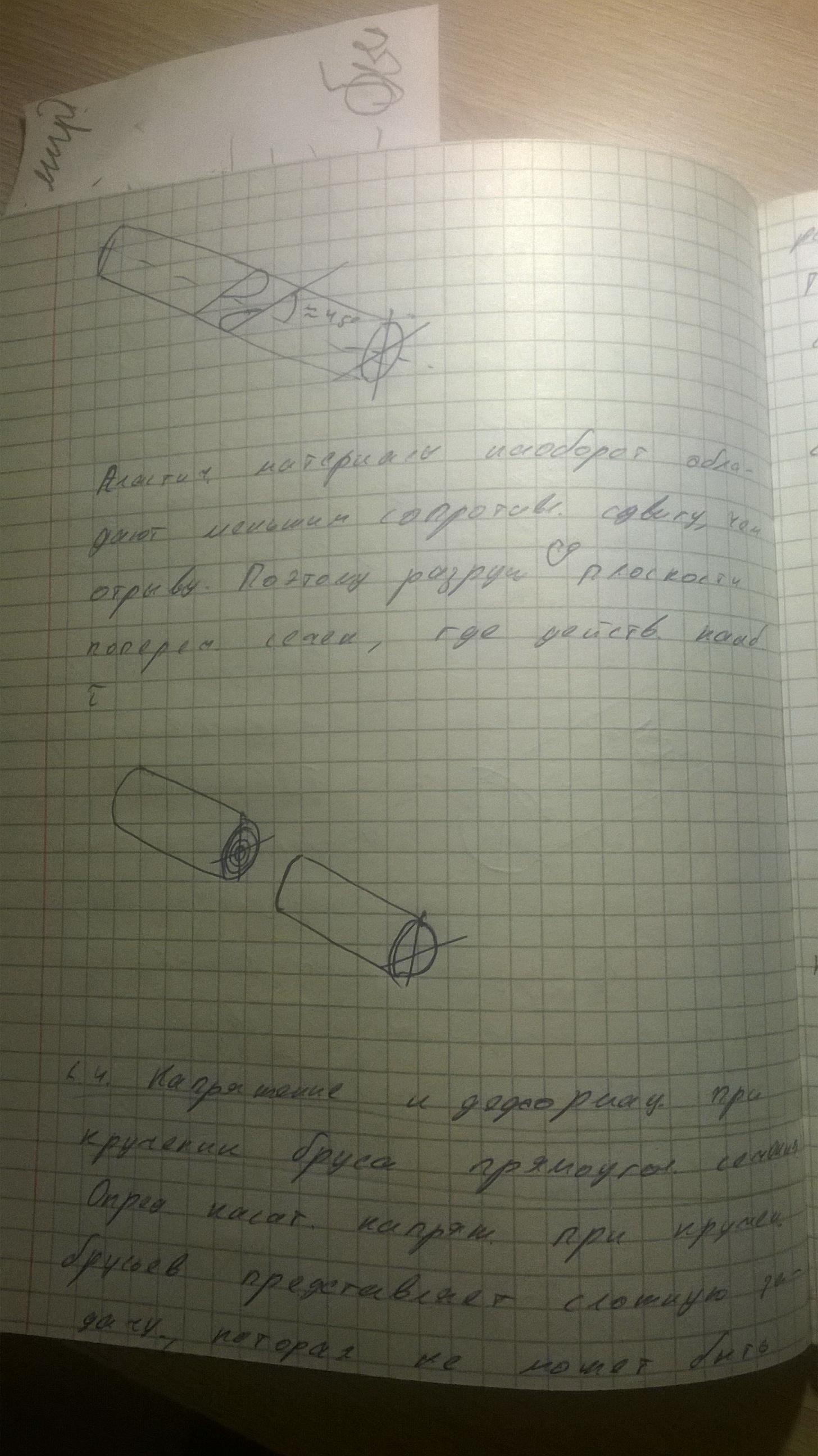
29. Вывести формулу для определения касательных напряжений при свободном (чистом) кручении тонкостенного бруса замкнутого сечения. -

30. Напряжения и деформации при кручении бруса прямоугольного сечения. -

29. Вывести формулу для определения угла закручивания j при свободном (чистом) кручении тонкостенного бруса замкнутого сечения. –

29. Вывести формулу для определения касательных напряжений при свободном кручении тонкостенного бруса открытого профиля. –

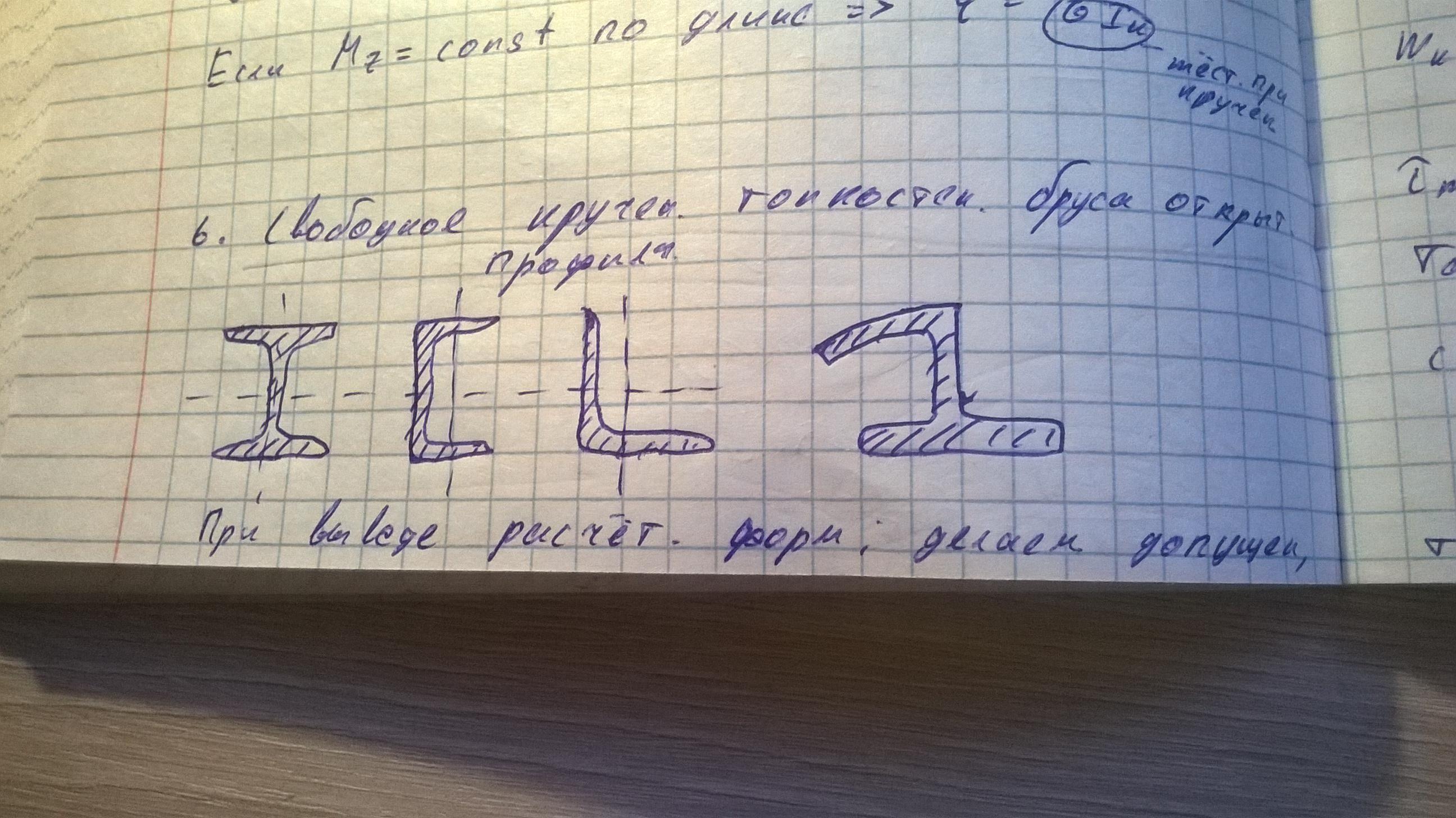
29. Вывести формулу для определения нормальных напряжений при чистом изгибе (геометрическое, физическое, статическое и синтезирующее уравнения). –

29. Вывести формулу Журавского для определения касательных напряжений при плоском поперечном изгибе. –