1.2. Метод амперметра и вольтметра

Можно измерить сопротивление и косвенно, используя закон Ома . Необходимые значения напряжения и силы тока получают с помощью вольтметра и амперметра. Однако невозможно собрать такую схему подсоединений этих приборов к измеряемому сопротивлению, в которой бы вольтметр измерял напряжение U, а амперметр в это же время ― силу тока I.

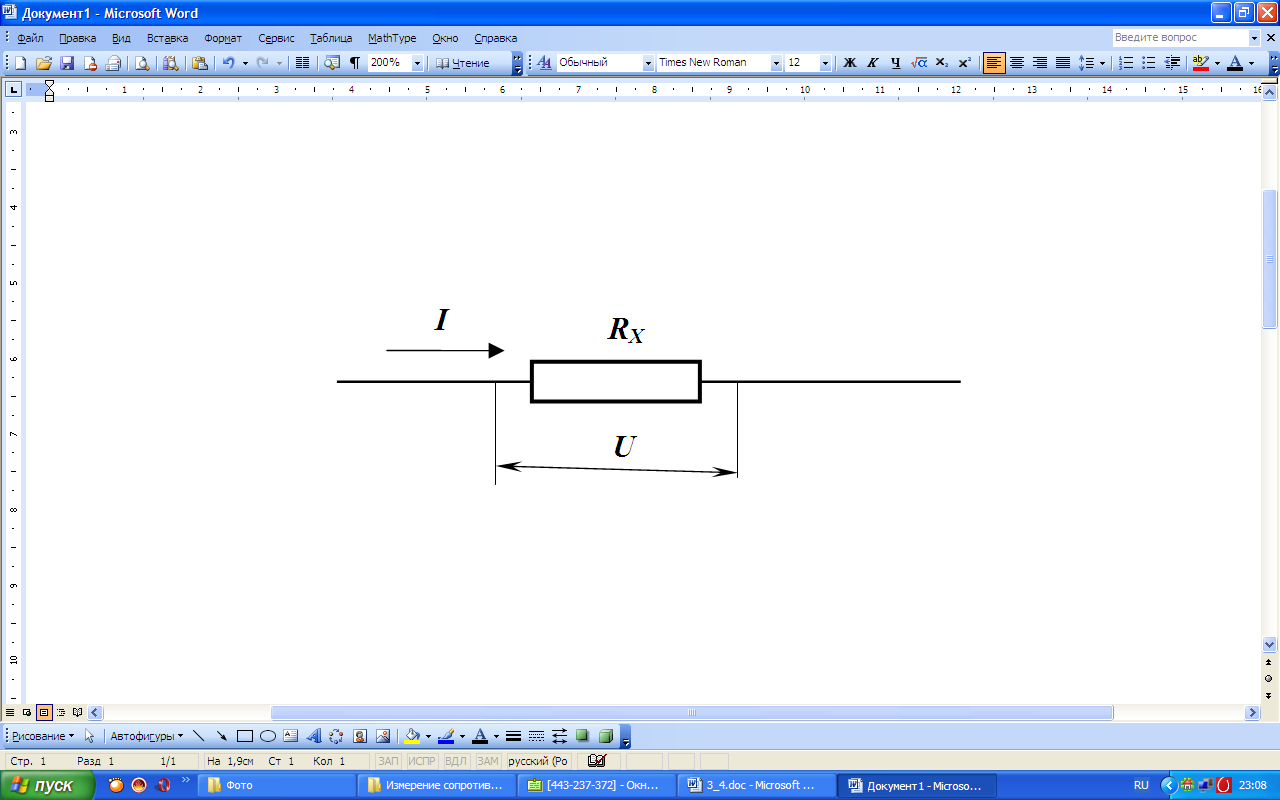
Рассмотрим схемы, применяемые в данной работе.

Существует два варианта схемы подсоединений. В первом из них амперметр измеряет силу тока I, протекающего через сопротивление, а вольтметр ― сумму напряжений на амперметре, U_A, и сопротивлении, U (рис. 2).

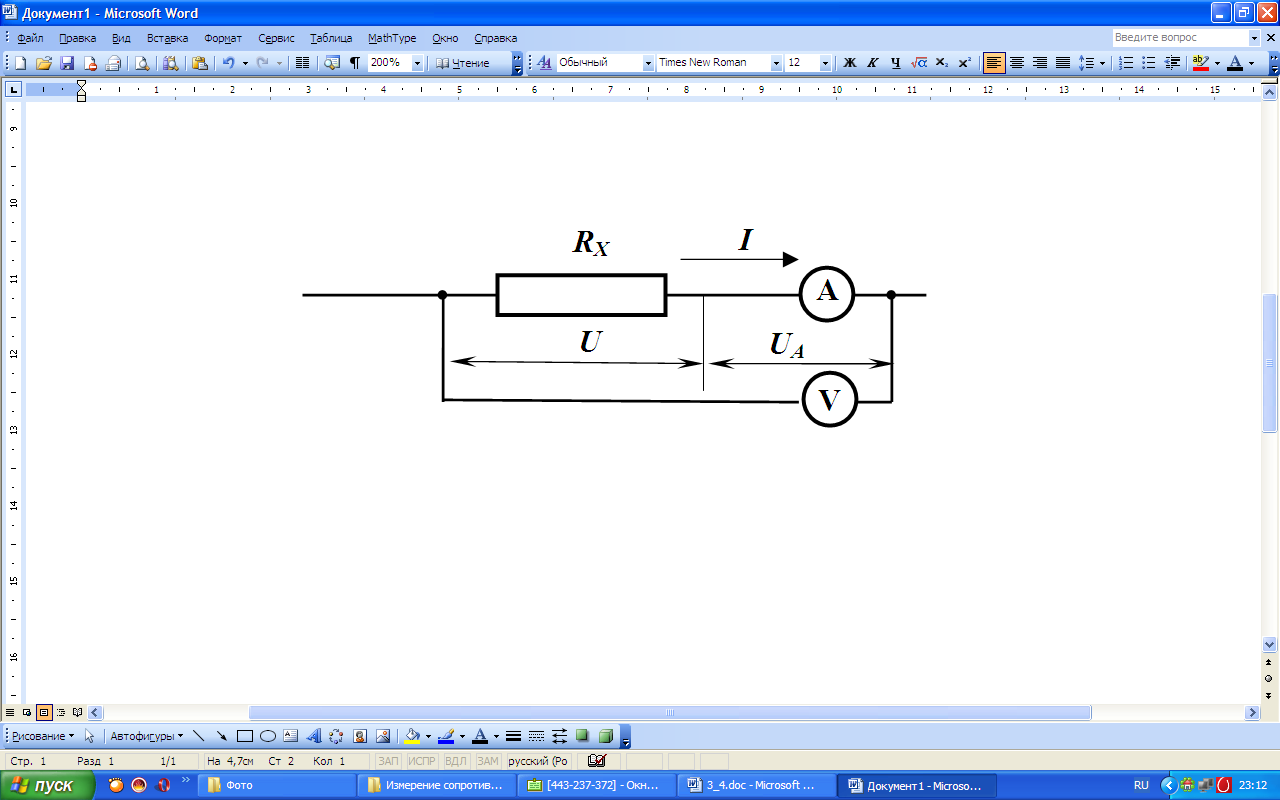
Рис. 2. Первый вариант схемы соединений

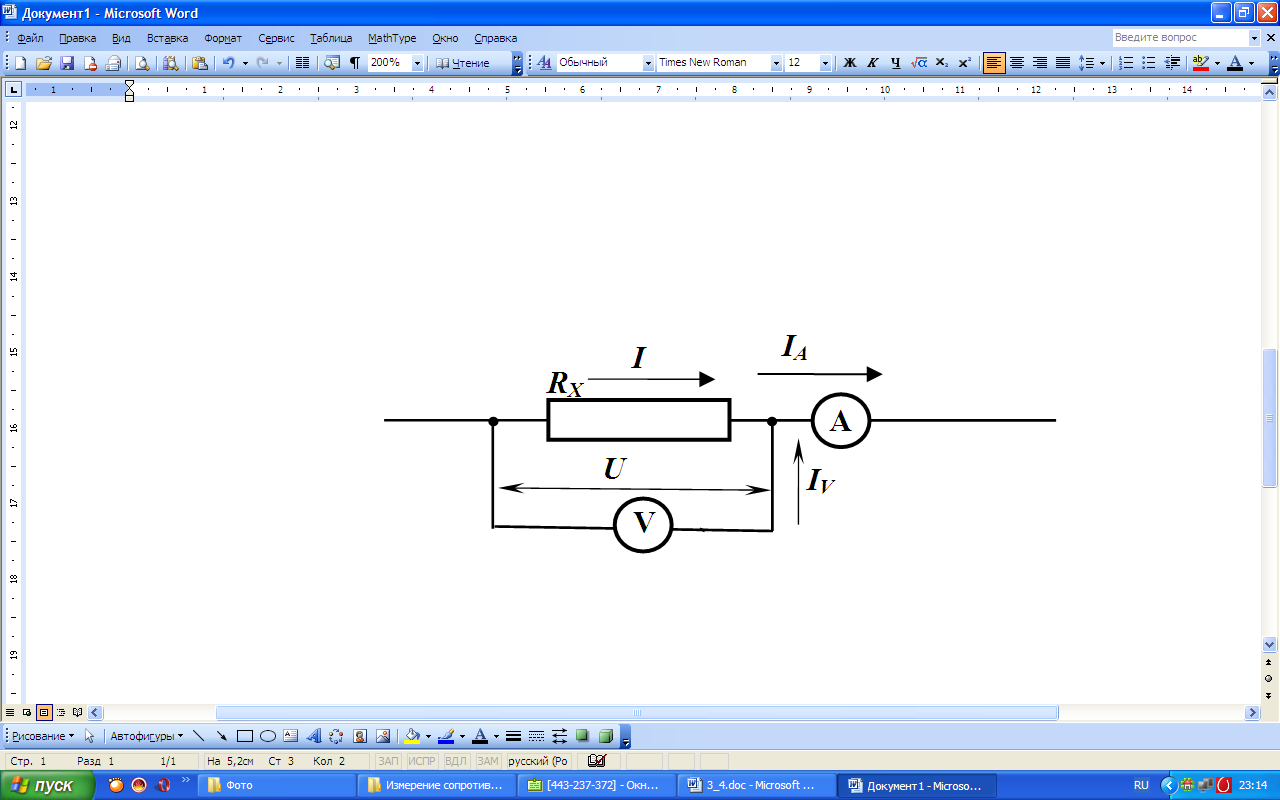
Рис. 3. Второй вариант схемы соединений

Во втором варианте схемы вольтметр измеряет напряжение на сопротивлении, U, а амперметр ― сумму сил токов, протекающих по сопротивлению, I, и по вольтметру, I_V, (рис. 3).

Если внутренние сопротивления вольтметра и амперметра известны, то с помощью законов Ома и Кирхгофа по результатам измерений можно вычислить значение искомого сопротивления.

Рассмотрим, как выполняется такой расчёт в первом варианте схемы. Обозначим отношение показания вольтметра, U_V, к показанию амперметра через R₁.

. (1)

Очевидно, что R₁.= R_А+ R_X, а искомое сопротивление

R_X = R₁ ― R_А. (1*)

Если же нам неизвестно значение сопротивления амперметра и в качестве результата измерений мы принимаем R₁, то мы завышаем истинное значение сопротивления на величину R_А, которая является систематической абсолютной погрешностью измерений, порождаемой особенностями первого варианта схемы. Относительная погрешность при этом будет

Рассмотрим расчёт значения искомого сопротивления R_X во втором варианте схемы. По закону Ома . Обозначим через R₂ отношение показания вольтметра к показанию амперметра:

. (2)

Теперь . (2*)

Если значение R_V неизвестно и в качестве результата измерения принять R₂, то будет допущена систематическая (связанная с особенностями этой схемы) погрешность, занижающая значение измеряемого сопротивления. Модуль абсолютной систематической погрешности

а модуль относительной систематической погрешности для второго варианта схемы

(выведите это самостоятельно!).

Выводы:

• Оба варианта схемы позволяют узнать величину измеряемого сопротивления, если известны значения внутреннего сопротивления амперметра (для первого варианта, формула (1*)) или вольтметра (для второго варианта, формула (2*)).

• Если значения внутренних сопротивлений приборов неизвестны, то приближённые значения измеряемого сопротивления содержат систематические погрешности, обусловленные схемами подключений приборов. Причём в первом варианте относительная погрешность уменьшается с возрастанием величины измеряемого сопротивления, а во втором ― увеличивается. Можно вывести, при каком измеряемом сопротивлении эти погрешности станут равными. Хорошим приближением к этому значению является .(Предлагаем получить это значение, учитывая то, что , самостоятельно!). Следовательно, в случае приближённых измерений сопротивлений следует использовать первую схему, а иначе ― вторую.