
Матан(ответы,)
.docx
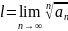
Тогда при l<1 ряд сходится, а при l>1, расходится.
При l=1 неопределено.
Даламбера:
Пусть
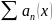 -положительный
ряд. Рассмотрим последовательность
-положительный
ряд. Рассмотрим последовательность
 .
Если начиная с некоторого номера
.
Если начиная с некоторого номера
 ,
если 0<q<1,
ряд сходится.
Раабе:
,
если 0<q<1,
ряд сходится.
Раабе:
Пусть существует
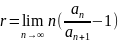 конечный или нет. Если r>1, ряд сходится,
если r<1
ряд расходится.
конечный или нет. Если r>1, ряд сходится,
если r<1
ряд расходится.
Интегральный признак Коши:
Ряд
сходится или расходится одновременно
с несобственным интегралом
 ,
где f(x)
определена для любого
,
где f(x)
определена для любого
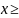 1
и
1
и
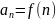
Теорема Лейбница для знакопеременных рядов.
Знакопеременный
ряд
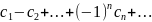 сходится, если:
сходится, если:
1)
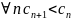
2)
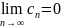
Признаки Абеля и Дирихле сходимости числового ряда.
Пусть
сходится, числа
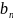 ограничены в совокупности:
ограничены в совокупности:
 )
и образует монотонную последовательность
, тогда ряд
)
и образует монотонную последовательность
, тогда ряд
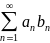 сходится
сходится
Умножение рядов. Теорема Коши.
Пусть даны 2 сходящихся ряда:
(1) и
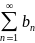 (2).
По ним составим таблицу:
(2).
По ним составим таблицу:
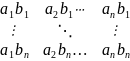
Произведением ряда (1) и ряда (2) называется ряд из всех элементов таблицы, взятых в любом заданном порядке.
Теорема Коши:
Если оба ряда (1) и (2) сходятся абсолютно, то их произведение сходится абсолютно и сумма произведения равна AB, где:
А= B=
Поточечная и равномерная сходимость (функциональных последовательностей и рядов).
Пусть дана
последовательность функций
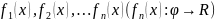
Последовательность
{ }
называется сходящейся в точке х из Х,
если сходится числовая последовательность
{
(х)}.
Множество Х таких точек называется
множеством сходимости функциональной
последовательности. На нем определена
функция:
}
называется сходящейся в точке х из Х,
если сходится числовая последовательность
{
(х)}.
Множество Х таких точек называется
множеством сходимости функциональной
последовательности. На нем определена
функция:
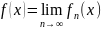 она называется
предельной.
она называется
предельной.
Сходимость
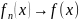 означает, что для фиксированного
х из Х
означает, что для фиксированного
х из Х
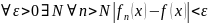
сходится к f, если:
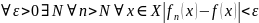
Признак Вейерштрасса равномерной сходимости
Пусть ряд
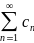 сходится и
сходится и
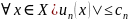 .
Тогда ряд
.
Тогда ряд
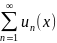 сходится равномерно на Х.
сходится равномерно на Х.
Теорема о почленном переходе к пределу.
Почленное интегрирование и дифференцирование рядов.
Теорема
1: Если
 ,
то степенной ряд
,
то степенной ряд
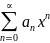 можно почленно интегрировать на [0, x]
можно почленно интегрировать на [0, x]
Теорема 2: Степенной ряд можно почленно дифференцировать на (–R, R)
Степенной ряд.
Степенным рядом наз-ся ряд вида:
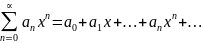 ,
,
где
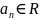 – постоянные коэф-ты и ряд вида
– постоянные коэф-ты и ряд вида
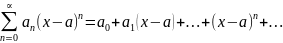
Промежуток сходимости степенного ряда.
Радиусом сходимости
степенного ряда наз-ся число R
такое, что при
ряд сходится, а при
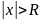 ряд расходится. Промежуток с концами
-R,R
(с включением концов или нет) наз-ся
промежутком сходимости степенного
ряда
ряд расходится. Промежуток с концами
-R,R
(с включением концов или нет) наз-ся
промежутком сходимости степенного
ряда
Теорема Коши-Адамара.
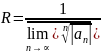 ,
R=
,
R=
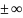 ,
если
,
если
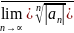 =0
R=
0, если
=0
R=
0, если
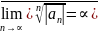
Ряд Тейлора. Ряды Тейлора элементарных функций.
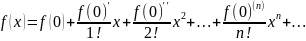 -
-
 ряд Тейлора
ряд Тейлора
