• „To nejlepší, co může člověk, který dává dárek, podle standardní mikroekonomické teorie spotřebitelské volby udělat s např. 10 $, je vybrat přesně to, co by si vybral obdarovaný."(p. 1328)

• Ve většině případů na tom bude obdarovaný hůř.

• Odhaduje náklady mrtvé váhy Vánoc na základě dotazníkového šetření mezi bakalářskými studenty na Yale.

• Dávání dárků ničí 10 % až 1/3 hodnoty dárku: ztráta min. 4 mld. $ (10 % odhadované ztráty mrtvé váhy z daně z příjmu)

• Nejhorší věcné dárky dává širší rodina - také dává nejčastěji peníze.

Shrnutí

• Optimální volba je spotřební koš náležející do rozpočtové množiny spotřebitele, který leží na nejvyšší indiferenční křivce.

• MRS se v optimu většinou rovná sklonu linie rozpočtu.

• Můžeme odhadnout užitkovou funkci ze spotřebitelských rozhodnutí a použít ji k hodnocení hospodářské politiky.

• Pokud každý čelí stejným cenám dvou statků, potom bude mít každý stejnou MRS mezi těmito statky.

Projevené preference

Ve druhé části přednášky se dozvíte,

• co to znamená, když je koš projevený jako preferovaný před jiným košem,

• jak můžeme získat preference z rozhodnutí spotřebitele,

• co je to slabý a silný axiom projevených preferencí.

Motivace projevených preferencí

5. předchozím výkladu jsme z preferencí odvozovali chování spotřebitele

   5. realitě ale nemůžeme preference přímo pozorovat.

Projevené preference pracují obráceně - z chování odvozují preference.

Pokud chceme odvodit preference z chování lidí, musíme předpokládat, že se preference v době, kdy pozorujeme toto chování, nemění.

5. této části přednášky také předpokládáme, že preference jsou striktně konvexní - tím dostaneme jediný poptávaný spotřební koš.

Myšlenka projevených preferencí

Jestliže vybereme (x1,x₂), když (y1, y₂) je dosažitelný, potom víme, že (x₁,x₂) je lepší než (y₁,y₂).

Formálněji: Jestliže vybereme (x₁, x₂) při cenách (p₁, p₂) a (y₁, y₂) je jiný koš, takový že p₁ x₁ + p₂x₂ ≥ p₁y₁ + p₂y₂, a jestliže spotřebitel vybírá nejpreferovanější spotřební koš, který si může dovolit, potom platí, že

(x₁, x₂) > (y₁, y₂).

Myšlenka projevených preferencí (pokračování)

Jestliže p₁ x₁ + p₂x₂ > p₁y₁ + p₂y₂, pak (x₁, x₂) je přímo projevený jako preferovaný před (y₁,y₂).

Pokud X je přímo projevený jako preferovaný před Y a Y je přímo projevený jako preferovaný před Z, pak vyplývá z tranzitivity, že X je nepřímo projevený jako preferovaný před Z.

Myšlenka projevených preferencí (pokračování)

Čím více pozorovaných voleb spotřebitele, tím lepší znalost preferencí.

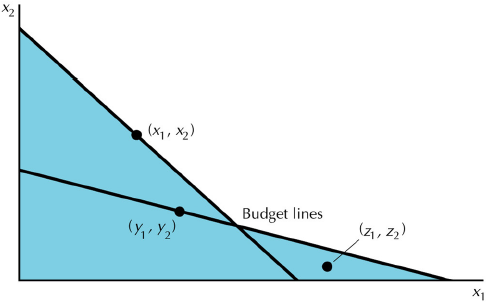
Tento graf používá poptávané koše k získání preferencí - indiferenční křivky leží mezi vystínovanými oblastmi.

Volba nekonzistentní s modelem spotřebitelské volby

Koš (x₁, x₂) v grafu je přímo projevený jako preferovaný před (y₁, y₂) a (y₁, y₂) je přímo projevený jako preferovaný před košem (x₁, x₂).

Formálněji: pro koš (x₁, x₂) nakoupený při cenách (p₁, p₂) a jiný koš (y₁, y₂) nakoupený při cenách (q₁, q₂) platí, že

p₁x₁ + p₂x₂ > p₁y₁ + p₂y₂ a q₁ y₁ + q₂y₂ > q₁x₁ + q₂x₂.

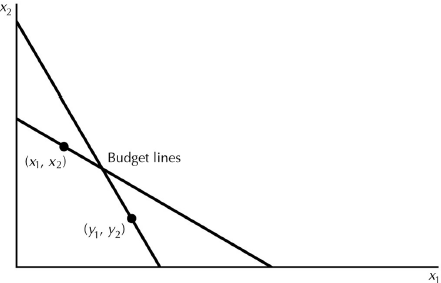
Slabý axiom projevených preferencí (WARP)

Slabý axiom projevených preferencí:

Jestliže (x1, x₂) je přímo projevený jako preferovaný před (y1, y₂), potom (y1, y₂) nemůže být přímo projevený jako preferovaný před (x₁, x₂).

Formálněji: pro každý koš (x₁, x₂) nakoupený při cenách (p₁, p₂) a jiný koš (y₁, y₂) nakoupený při cenách (q₁, q₂) platí že, jestliže

p₁ x₁ + p₂ x₂ > p₁ y₁ + p₂ y₂,

pak nesmí platit, že

q₁ y₁ + q₂ y₂ > q₁ x₁ + q₂ x₂.

Jak testovat WARP?

Jak systematicky testovat WARP? Máme následující spotřební data:

Tabulka dole ukazuje náklady košů 1, 2 a 3 při různých cenách.