Моделирование рядов распределения.
Выдвинем
гипотезу о том, что распределение в
совокупности подчиняется нормальному
закону. Воспользуемся для проверки
гипотезы критерием согласия Пирсона
(показатель
),
для чего возьмем за основу вариационный
ряд, составленный ранее. Необходимо
рассчитать и оценить отклонения
фактических значений частот появления
признака от тех значений, которые могли
бы быть в случае нормального распределения.
Значение критерия согласия Пирсона ( ) вычисляется по формуле:
=
(16)
где k – количество выделенных интервалов;
– частота
попадания признака в j-й
интервал соответственно в эмпирическом
и теоретическом рядах распределения.
Эмпирическая частота – частота
распределения признака в фактическом
вариационном ряду, а теоретическая
частота определяется по формуле:
=
∑
×
×
(t)
(17)
где l– длина интервала;
σ – среднее квадратическое отклонение признака;
(t) – плотность вероятности нормального нормированного распределения, определяющаяся по значению нормированного отклонения (t), которое рассчитывается по формуле:
t
=
(18)
где – середина интервала;
Для расчетов возьмем данные, полученные выше:
Средняя величина: = 102 больничных койки;
Среднее квадратическое отклонение: σ = 18,08 больничных коек на 10 000 тысяч человек.
Длина интервала: l = 18
Рассчитаем значения нормированного отклонения для каждого интервала с помощью таблицы:
Таблица 3.1. – Расчет значений нормированного отклонения
-
Номер пункта по порядку
Число больничных коек на 10 000 человек населения
Частота появления признака
Середина интервала
Отклонение
t =
1
40 – 58
1
49
-53
-2,93
2
58 – 76
2
67
-35
-1,93
3
76 – 94
20
85
-17
0,94
4
94 – 112
45
103
1
0,05
5
112 – 130
10
121
19
1,05
6
130 – 148
3
139
37
2,04
7
148 – 166
1
157
55
3,04
8
166 – 184
1
175
73
4,03
Значения нормированного отклонения для каждого интервала считаем по формуле (18):
=
= –2,93;
=
= –1,93 и т.д.
По рассчитанным значениям нормированного отклонения находим соответствующие значения плотности вероятности нормального распределения.
Например:
= – 2,93, следовательно, плотность вероятности (t) = 0,0055
= – 1,93, следовательно, плотность вероятности (t) = 0,0620 и так далее.
Теперь рассчитаем значения теоретической частоты:
=
83 ×
×
0,0055 = 0,4
=
83 ×
×
0,0620 = 5
Расчеты значений теоретической частоты сведены в таблицу 3.2.
Таблица 3.2 – Расчет значений теоретических частот распределения признака
Номер пункта по порядку |
Число больничных коек на 10 000 человек населения |
Середина интервала
|
Отклонение t = |
Плотность вероятности (t) |
Теоретическая частота
|
1 |
40 – 58 |
49 |
-2,93 |
0,0055 |
0,4 |
2 |
58 – 76 |
67 |
-1,93 |
0,0620 |
5 |
3 |
76 – 94 |
85 |
0,94 |
0,2565 |
21 |
4 |
94 – 112 |
103 |
0,05 |
0,3988 |
33 |
5 |
112 – 130 |
121 |
1,05 |
0,2299 |
19 |
6 |
130 – 148 |
139 |
2,04 |
0,0498 |
4 |
7 |
148 – 166 |
157 |
3,04 |
0,0039 |
0,3 |
8 |
166 – 184 |
175 |
4,03 |
0,0001 |
0 |
Для проверки гипотезы о нормальном распределении по критерию Пирсона интервалы со значением теоретической частоты менее 5 необходимо объединить с соседними.
После объединения получится таблица 3.3
Таблица 3.3 - Расчет значений теоретических частот распределения признака после объединения интервалов.
Число больничных коек на 10 000 человек населения |
Середина интервала
|
Количество субъектов
|
Отклонение t = |
Плотность вероятности (t) |
Теоретическая частота
|
40-76 |
58 |
3 |
-2,07 |
0,0468 |
6 |
76-94 |
85 |
20 |
-0,88 |
0,2709 |
18 |
94-112 |
103 |
45 |
-0,08 |
0,3977 |
26 |
112-184 |
148 |
15 |
1,90 |
0,0656 |
17 |
Так же необходимо снова рассчитать среднюю величину и среднее квадратическое отклонение.
Новая средняя:
=
= 105
=
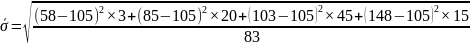22,6
Рассчитываем фактическое значение . Расчеты наглядно представлены в таблице 3.3.
Таблица 3.4 – Расчет фактического значения критерия согласия Пирсона
Номер пункта по порядку |
Число больничных коек на 10 000 человек населения |
|
|
|
|
|
1 |
40 – 76 |
3 |
6 |
-3 |
9 |
1,5 |
2 |
76 - 94 |
20 |
18 |
2 |
4 |
0,2 |
3 |
94-112 |
45 |
26 |
19 |
361 |
13,9 |
4 |
112-184 |
15 |
17 |
-2 |
4 |
0,2 |
Итого: |
83 |
67 |
Х |
Х |
15,8 |
|
Таким образом, по расчетам = 15,8
Сравниваем рассчитанное и табличное значения . Табличное значение определяется по «Распределению Пирсона» по двум входным параметрам: число степеней свободы (d.f.) и степени значимости (α). Число степеней свободы при проверке гипотезы о нормальном характере распределения равно:
d.f. = к – 3
где к – число интервалов в вариационном ряду.
По значениям α = 0,05 и d.f. = 4 – 3 = 1 находим χ2табл = 3,841
Фактическое значение больше табличного (15,8 > 3,841), следовательно, мы отклоняем гипотезу о нормальном распределении.