Дискретная математика, ВМСиС, Заочка, Контрольная, 2011, Вариант № 32
.docxВариант №32
1. В графе, представленном следующей матрицей смежности, найти все максимальные независимые множества.
-
2 3 4 5 6 7 8 9 10
0 0 1 0 1 1 0 1 0 1 1
0 0 0 1 1 0 0 0 0 0 2
1 0 0 1 0 1 1 0 0 0 3
0 1 1 0 1 1 0 1 1 1 4
1 1 0 1 0 0 1 1 1 0 5
1 0 1 1 0 0 0 0 1 1 6
0 0 1 0 1 0 0 0 1 1 7
1 0 0 1 1 0 0 0 0 0 8
0 0 0 1 1 1 1 0 0 1 9
1 0 0 1 0 1 1 0 1 0 10
Решение:
Построим последовательность
(описана в методичке), где
 представляет совокупность независимых
множеств:
представляет совокупность независимых
множеств:


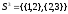
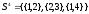

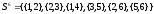

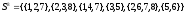
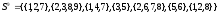

Таким образом, максимальными независимыми множествами являются
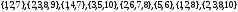
2. Получить минимальную систему ДНФ для следующей системы полностью определенных булевых функций:
x1 x2 x3 x4 f1 f2 f3
0 1 0 1 0 0 1
1 0 1 0 1 0 1
1 1 1 0 0 1 0
0 0 0 0 0 1 0
1 0 0 0 , 1 1 0 .
1 1 0 0 1 1 0
0 1 0 0 0 1 0
0 0 1 0 0 0 1
Решение.
Минимизируем данную систему ДНФ методом Квайна-МакКласки. Получаем следующую последовательность пар матриц.
|
Х1 |
Х2 |
Х3 |
Х4 |
|
f1 |
f2 |
f3 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
2 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
3* |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
4* |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
5* |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
6* |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
7* |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
8* |
0 |
0 |
1 |
|
Х1 |
Х2 |
Х3 |
Х4 |
|
f1 |
f2 |
f3 |
|
1 |
0 |
- |
0 |
1 |
1 |
0 |
0 |
|
- |
0 |
1 |
0 |
2 |
0 |
0 |
1 |
|
1 |
1 |
- |
0 |
3 |
0 |
1 |
0 |
|
- |
0 |
0 |
0 |
4* |
0 |
1 |
0 |
|
0 |
- |
0 |
0 |
5* |
0 |
1 |
0 |
|
1 |
- |
0 |
0 |
6 |
1 |
1 |
0 |
|
- |
1 |
0 |
0 |
7* |
0 |
1 |
0 |
|
Х1 |
Х2 |
Х3 |
Х4 |
|
f1 |
f2 |
f3 |
|
- |
- |
0 |
0 |
1 |
0 |
1 |
0 |
Получили сокращенную систему ДНФ, которая содержит строки, не отмеченные знаком «*»
|
Х1 |
Х2 |
Х3 |
Х4 |
|
f1 |
f2 |
f3 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
2 |
1 |
0 |
1 |
|
1 |
0 |
- |
0 |
3 |
1 |
0 |
0 |
|
- |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
|
1 |
1 |
- |
0 |
5 |
0 |
1 |
0 |
|
1 |
- |
0 |
0 |
6 |
1 |
1 |
0 |
|
- |
- |
0 |
0 |
7 |
0 |
1 |
0 |
Теперь проведем второй этап минимизации, который сводится к задаче покрытия.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
5 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
7 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
Кратчайшее строчное покрытие приведенной матрицы соответствует двум кратчайшим системам ДНФ, представляемыми следующими матрицами:
|
Х1 |
Х2 |
Х3 |
Х4 |
|
f1 |
f2 |
f3 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
2 |
1 |
0 |
1 |
|
- |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
|
1 |
1 |
- |
0 |
5 |
0 |
1 |
0 |
|
1 |
- |
0 |
0 |
6 |
1 |
1 |
0 |
|
- |
- |
0 |
0 |
7 |
0 |
1 |
0 |
|
Х1 |
Х2 |
Х3 |
Х4 |
|
f1 |
f2 |
f3 |
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
- |
0 |
3 |
1 |
0 |
0 |
|
- |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
|
1 |
1 |
- |
0 |
5 |
0 |
1 |
0 |
|
1 |
- |
0 |
0 |
6 |
1 |
1 |
0 |
|
- |
- |
0 |
0 |
7 |
0 |
1 |
0 |
3. Закодировать состояния методом «желательных соседств» для автомата, заданного следующей таблицей, и получить соответствующую минимальную систему ДНФ
|
|
00 |
01 |
10 |
|
1 |
1,0 |
2,- |
- |
|
2 |
4,1 |
- |
3,0 |
|
3 |
2,1 |
3,1 |
1,- |
|
4 |
- |
- |
1,0 |
Решение.
Построим автомат с минимальным числом состояний.
Явно
несовместимыми являются пары
 и
и
 .
Пары
.
Пары
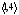 и
и
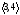 являются явно совместимыми. Цепь,
порождаемая парой
являются явно совместимыми. Цепь,
порождаемая парой
 ,
содержит несовместимую пару
,
содержит несовместимую пару
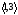 ,
поэтому она тоже несовместима. Таким
же образом несовместимы пары
,
поэтому она тоже несовместима. Таким
же образом несовместимы пары
 .
В итоге получаем следующую матрицу
совместимости:
.
В итоге получаем следующую матрицу
совместимости:
|
2 |
3 |
4 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
0 |
2 |
|
|
|
1 |
3 |
Итак,
получаются совместимые пары
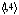 и
и
 .
.
В
результате правильную минимальную
группировку
 ,
,
 и
и
 .
.
В результате минимизации заданного автомата получаем автомат с тремя состояниями, таблицей переходов и выходов которого является:
|
|
00 |
01 |
10 |
|
1 |
1,0 |
2,- |
1,0 |
|
2 |
1,1 |
- |
3,0 |
|
3 |
2,1 |
3,1 |
1,- |
Вычислим
значения
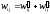 ,
где
,
где
 - число столбцов таблицы переходов, в
которых строки
- число столбцов таблицы переходов, в
которых строки
 и
и
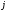 имеют одинаковые элементы, т.е. число
значений переменной
имеют одинаковые элементы, т.е. число
значений переменной
 ,
при которых
,
при которых
 .
.
Таблица переходов:
|
|
00 |
01 |
10 |
|
1 |
1 |
2 |
1 |
|
2 |
1 |
- |
3 |
|
3 |
2 |
3 |
1 |
А
 ,
где
,
где
 - число состояний автомата,
- число состояний автомата,
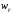 - число пар вида
- число пар вида
 ,
причем
,
причем
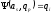 и
и
 ,
а входные символы
,
а входные символы
 и
и
 имеют соседние коды, удобно задать в
виде таблицы:
имеют соседние коды, удобно задать в
виде таблицы:
|
|
|
|
|
|
4 |
3 |
0 |
|
|
|
1 |
0 |
|
|
|
|
0 |
|
где
строки и столбцы соответствуют состояниям
автомата, а
 - фиктивное состояние.
- фиктивное состояние.
На
первом шаге получаем два одномерных
гиперкуба с максимальными значениями
весов
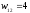 и
и
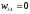 .
.

А теперь выберем один двумерный гиперкуб, для которого выбираются два ребра с максимальной суммой весов.
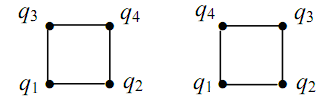

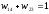
Получаем один двумерный гиперкуб с максимальным весом добавленных ребер.
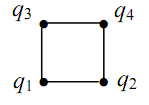
Теперь можем составить таблицу кодирования состояний:
|
|
|
|
|
|
0 |
0 |
|
|
1 |
0 |
|
|
0 |
1 |
Минимизированная система булевых функций, описывающая заданное поведение, представляется следующими матрицами:
|
Х1 |
Х2 |
Z1 |
Z2 |
|
|
|
Y |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
- |
|
0 |
1 |
1 |
0 |
|
- |
- |
- |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
|
0 |
0 |
- |