
2. Явище самоіндукції. Індуктивність. Енергія магнітного поля
Якщо по замкненому контуру проходить змінний струм, то магнітний потік, що пронизує контур, змінюється. Тому згідно із законом електромагнітної індукції Фарадея в цьому ж провіднику виникає ЕРС індукції. Це явище називають самоіндукцією. Під час самоіндукції провідний контур відіграє подвійну роль: по ньому проходить струм, що викликає індукцію, і в ньому ж з'являється ЕРС індукції ei.
Згідно з правилом Ленца в момент збільшення сили струму напруженість електричного вихрового поля напрямлена проти струму. Отже, в цей момент самоіндукція перешкоджає наростанню струму. Навпаки, в момент зменшення струму самоіндукція його підтримує.
Це приводить до того, що під час замикання кола зі сталою ЕРС певне значення струму встановлюється не одразу, а поступово, з часом (рис.4.4.17). Під час вимикання джерела струм в замкненому контурі не зникає миттєво. При цьому ЕРС самоіндукції може перевищувати ЕРС джерела, оскільки зміна струму і, отже, його магнітного поля під час вимкнення джерела відбувається дуже швидко. Цим міркуванням можна знайти експериментальне підтвердження. Нехай дві однакові лампочки Л1 і Л2 з'єднані паралельно через резистор R і котушку індуктивності L в колі з джерелом постійного струму Б і перемикачем К (рис.4.4.18). Під час замикання кола ключем К лампочка Л1 загорається миттєво. Лампочка Л2 загоряється із запізненням. Це пояснюється тим, що сила струму на ділянці кола з котушкою через явище самоіндукції встановлюється не одразу, а поступово (рис.4.4.17).
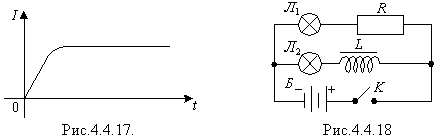
Під час розмикання кола ключем К спалахнуть обидві лампочки. У цьому випадку струм у колі підтримується ЕРС самоіндукції, що виникає під час зменшення магнітного потоку в котушці.
Явище самоіндукції подібне до явища інерції в механіці. Унаслідок самоіндукції під час замикання кола сила струму не одразу набуває максимального значення. І, навпаки, під час вимикання джерела струм не зникає одразу, а самоіндукція підтримує його деякий час, не зважаючи на опір кола. Мірою "інертності" контуру відносно змін сили струму в ньому (аналогічно масі тіла в механіці) в електродинаміці відіграє індуктивність або коефіцієнт самоіндукції контуру L. Це коефіцієнт пропорційності між струмом у провідному контурі і створеним ним магнітним потоком, що пронизує цей контур:
Ф = LI. (4.4.8)
Використовуючи закон електромагнітної індукції (4.4.4) і вираз (4.4.8) за умови, що форма контуру залишається незмінною, дістаємо рівність
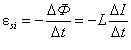 .
(4.4.9)
.
(4.4.9)
Індуктивність, як і електроємність, залежить від геометричних чинників: від розмірів провідника і його форми, але не залежить безпосередньо від сили струму в провіднику. Крім того, індуктивність залежить від магнітних властивостей середовища, в якому знаходиться провідник. Наприклад, індуктивність соленоїда (довгої котушки, обкрученої провідником): L = mm0n2V,
де
m0 - магнітна стала; n - кількість
витків на одиницю довжини (![]() );
V = Sl - об'єм соленоїда.
);
V = Sl - об'єм соленоїда.
З формули (4.4.9) випливає, що індуктивність - це скалярна фізична величина, яка чисельно дорівнює ЕРС самоіндукції, що виникає в контурі внаслідок зміни струму на 1 А за 1 с.
Одиниця індуктивності в СІ - генрі (Гн). Індуктивність провідника дорівнює 1 Гн, якщо в ньому із зміною сили струму на 1 А за 1 с виникає ЕРС самоіндукції 1 В:
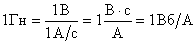 .
.
Явище самоіндукції відіграє дуже важливу роль в електротехніці й радіотехніці. Індуктивність кола істотно впливає на проходження в ньому змінного електричного струму.
Повернемося до досліду (рис.4.4.18). Під час розмикання кола лампа розжарення Л1, ввімкнена паралельно котушці, дає короткотривалий спалах. Струм у колі виникає під дією ЕРС самоіндукції. Джерелом енергії, що виділяється при цьому в електричному колі, є магнітне поле котушки.
Енергію магнітного поля котушки індуктивності знайдемо, виходячи з таких міркувань. Нехай після розмикання кола струм зменшується з часом за лінійним законом. У цьому разі ЕРС самоіндукції має постійне значення, що дорівнює
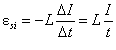 ,
,
де t - час, за який сила струму в колі лінійно зменшується від початкового значення І до 0.
За цей час в колі проходить електричний заряд
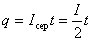 .
.
Робота електричного струму при цьому
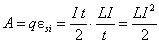 .
.
Ця робота виконується за рахунок енергії магнітного поля котушки індуктивності.
Енергія Wм магнітного поля котушки індуктивності дорівнює половині добутку її індуктивності на квадрат сили струму в ній:
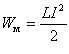 .
.
Як і у випадку з конденсатором, ця енергія міститься безпосередньо в об'ємі магнітного поля, а густина енергії wм = Wм за розрахунками
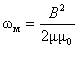 ,
,
де m0 - магнітна стала, значення якої в СІ дорівнює 4p·10-7 = H/A2. Цей вираз справедливий не тільки для однорідного поля, але і для довільних змінних магнітних полів.
3. Провідник, c протікає по ньому електричним струм, завжди оточений магнітним полем, причому магнітне поле зникає і з'являється разом із зникненням і появою струму. Магнітне поле, подібно до електричного, є носієм енергії. Логічно припустити, що енергія магнітного поля збігається з роботою, що витрачається струмом на створення цього поля. Розглянемо контур індуктивністю L, по якому протікає струм I. З цим контуром зчеплений магнітний потік Ф = LI, оскільки індуктивність контуру незмінна, то при зміні струму на dI магнітний потік змінюється на dФ = LdI. Але для зміни магнітного потоку на величину dФ слід зробити роботу dА = IdФ = LIdI. Тоді робота зі створення магнітного потоку Ф дорівнює робота зі створення магнітного потоку Значить, енергія магнітного поля, яке пов'язане з контуром, енергія магнітного поля (1) Енергію магнітного поля можна розглядати як функцію величин, які характеризують це поле в навколишньому просторі. Для цього розглянемо окремий випадок - однорідне магнітне поле всередині довгого соленоїда. Підставивши у формулу (1) формулу індуктивності соленоїда, знайдемо енергія магнітного поля Так як I = Bl / (μ0μN) і В = μ0μH, то енергія магнітного поля (2) де Sl = V - об'єм соленоїда. Магнітне поле всередині соленоїда однорідне і зосереджено всередині нього, тому енергія (2) укладена в обсязі соленоїда і має з нього однорідний розподіл з постійною об'ємною щільністю об'ємна щільність енергії магнітного поля (3) Формула (3) для об'ємної густини енергії магнітного поля має вигляд, аналогічний висловом для об'ємної густини енергії електростатичного поля, з тією відмінністю, що електричні величини замінені в ньому магнітними. Формула (3) виводилася для однорідного поля, але вона вірна і для неоднорідних полів. Формула (3) справедлива тільки для середовищ, для яких лінійна залежність У від Н, тобто воно стосується лише пара-і діамагнетиках.
4. Причина возникновения электрического тока в неподвижном проводнике - электрическое поле. Всякое изменение магнитного поля порождает индукционное электрическое поле независимо от наличия или отсутствия замкнутого контура, при этом если проводник разомкнут, то на его концах возникает разность потенциалов; если проводник замкнут, то в нем наблюдается индукционный ток.
Индукционное электрическое поле является вихревым. Направление силовых линий вихревого эл. поля совпадает с направлением индукционного тока Индукционное электрическое поле имеет совершенно другие свойства в отличии от электростатического поля.
Перше рівняння Максвелла.
Перше рівняння
Максвелла випливає із закону Фарадея
і зв'язує напруженість поля електромагнітної
індукції з індукцією змінного магнітного
поля
![]() .
Дійсно, якщо
.
Дійсно, якщо
![]() напруженість
індукованого електричного поля, що діє
в контурі LS,
то електрорушійна сила індукції у
контурі дорівнює
напруженість
індукованого електричного поля, що діє
в контурі LS,
то електрорушійна сила індукції у
контурі дорівнює
![]()
а магнітний потік і швидкість його зміни можна записати у вигляді
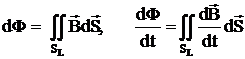
Тепер, зважаючи на закон Фарадея
![]()
![]() ,
,
можна записати рівність
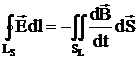 ,
(10)
,
(10)
яка представляє собою перше рівняння Максвелла в інтегральній формі.
Застосовуючи теорему Стокса (3), ліву частину (10) можна записати у вигляді
![]() .
(11)
.
(11)
Підставляючи цей вираз в інтегральне рівняння, одержимо з нього перше диференціальне рівняння Максвелла
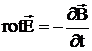 .
(12)
.
(12)
У цьому рівнянні ми вжили позначення частинної похідної по часу від індукції магнітного поля , яка є функцією багатьох змінних – часу й координат.
