Федеральное агентство по образованию

ГОУ ВПО ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Кафедра МиАС

Методические указания

к лабораторной работе № 4

« Исследование неразветвленной электрической цепи однофазного

Синусоидального тока»

для студентов инженерных специальностей

очной и заочной формы обучения

Составили:

Шулаева Л.В., Кириллова Р.Д.

Тюмень 2009 г.

Наименование учебно-методического материала: Шулаева Л.В., Кириллова Р.Д.

Методические указания к лабораторной работе № 4 « Исследование неразветвленной электрической цепи однофазного синусоидального тока» для студентов инженерных специальностей очной и заочной формы обучения.

Тюмень ТюмГАСУ, 2009 г. стр. 16

Рецензент___________зав. кафедры информатики к.т.н. Третьяков П.Ю.

(степень, звание, фамилия, имя, отчество)

Учебно-методический материал утвержден на заседании кафедры:

Протокол №___________________от _________2009 г.

Учебно-методический материал утвержден на УМС университета:

Протокол №___________________от___________2009 г.

Тираж____________________________________________экземпляров.

СОДЕРЖАНИЕ

1. Цель работы___________________________________________________4_

2.Основные теоретические положения_______________________________4

3. Резонанс напряжений___________________________________________9

4.Порядок выполнения работы_____________________________________13

5.Содержание отчета_____________________________________________14

6.Контрольные вопросы___________________________________________15

7. Библиографический список______________________________________15

1. Цель работы.

1. Проверка применимости законов Кирхгофа для цепей однофазного переменного тока.

- Убедиться, что при последовательном соединении электроприёмников полное напряжение в цепи равно геометрической сумме падений напряжения на участках цепи (второй закон Кирхгофа).

2. Исследовать влияние изменения одного из параметров цепи – реактивного емкостного сопротивления x_c - на величину тока, потребляемого цепью (резонанс напряжений).

2. Основные теоретические положения.

В настоящей работе исследуется неразветвленная (последовательное соединение приемников) электрическая цепь однофазного переменного синусоидального тока, содержащая активное, реактивное индуктивное, реактивное емкостное сопротивления (Рис.1).

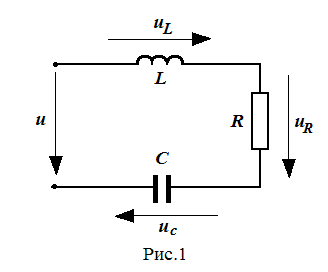
Под действием переменного синусоидального напряжения, приложенного к цепи, в ней возникает ток, изменяющийся во времени по синусоидальному закону. Аналитически его можно описать выражением:

i =I_m sinωt (1)

Проходя по элементам цепи, ток создает на них падения напряжения, мгновенные значения которых равны:

(2)

Из полученных выражений (2) для мгновенных значений падений напряжения можно сделать выводы:

1. – падение напряжения на катушке индуктивности u_L в своих изменениях опережает по фазе изменения тока на (90º), т.е. угол сдвига фаз φ_L = + ;

2. – падение напряжения на конденсаторе u_С отстает по фазе от тока на (90º), т.е. угол сдвига фаз φ_С = (- );

3. – падение напряжения на резисторе u_R совпадает по фазе с током, т.е.угол сдвига фаз φ_R = 0º;

4. Амплитудные значения напряжений равны:

U_Lm = I_LmX_L; U_Сm = I_СmX_С; U_Rm = I_RmR; (3)

Для последовательного соединения элементов (Рис.1)

II закон Кирхгофа можно записать в трех видах:

u = u_L + u_С + u_R - для мгновенных значений; (4)

Ů = Ů _Lm + Ů_mL + Ů_mR - для амплитудных значений (в векторной форме); (5)

Ů = Ů_L + Ů_C + Ů_R - для действующих значений(в векторной

форме); (6)

На основании II закона Кирхгофа строится векторная диаграмма для амплитудных значений.

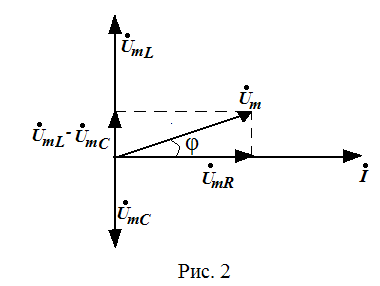
На практике чаще строится векторная диаграмма для действующих значений. Для этого уравнение (5) надо разделить на .

Для удобства суммирования можно строить векторы, пользуясь правилом многоугольника: каждый последующий вектор строится от конца предыдущего. Такая диаграмма называется топографической (Рис. 3).

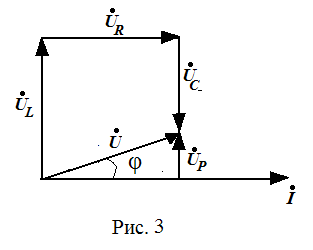
Вектор Ů_Р = Ů_L + Ů_C – вектор полного реактивного напряжения.

Следует учесть, что в данном случае активная составляющая Ů_а вектора полного напряжения совпадает с вектором Ů_R (Ů_а = Ů_R).

Из векторной диаграммы (Рис. 3) видно, что:

, (7)

т.к. U_R =I·R; U_L =I·X_L; U_C =I·X_С, (из формулы (3), поделив величины на ),

получаем:

U = I· (8)

Из формулы (8) выразим силу тока

- закон Ома (9)

где - (10)

полное сопротивление цепи переменного тока с последовательным соединением приемников.

Если в цепи несколько активных и реактивных элементов, то параметры R, X_L, X_C в выражении (10) следует рассматривать как соответствующие суммы:

(11)

Из диаграммы (Рис. 3) следует, что

(12)

Кроме того, видно, что в зависимости от величины U_L и U_С , напряжение U может отставать, опережать или совпадать по фазе с током I.

Если U_L > U_С , а это будет тогда, когда X_L > X_С, т.е. полное сопротивление Z – активно – индуктивное, а напряжение опережает по фазе ток (φ > 0).

Если U_С > U_L, (т.е. X_С > X_L), полное сопротивление Z – активно – емкостное, а напряжение отстает по фазе от тока (φ < 0).

Если U_L = U_С, (т.е. X_L = X_С), полное сопротивление Z = R – активное, а напряжение совпадает по фазе с током (φ = 0).

В цепях переменного тока протекают более сложные энергетические процессы, обусловленные наличием разнородных элементов: активного – R, реактивных X_L и X_С. На активном элементе – резисторе – происходит необратимое преобразование энергии электрического тока в другие формы энергии (в основном, в тепловую). Скорость такого преобразования – активная мощность – выражается следующим соотношением:

P = I²R =IU_R= IUcos φ (Вт, кВТ) (13)

На реактивных элементах L (катушка индуктивности) и C (конденсатор) происходит обратимый процесс преобразования энергии электрического тока в энергию магнитного поля (на катушке) и электрического поля (на конденсаторе). Энергия как бы совершает колебания между источником и реактивной нагрузкой.

Интенсивность таких колебаний количественно оценивается

реактивной мощностью:

Q_L = I² X_L = IU_L = IUsin φ (ВАР, кВАР) (14)

– реактивная индуктивная мощность;

Q_С = I² X_С = IU_C = IUsin φ (ВАР, кВАР) (15)

- реактивная емкостная мощность.

Полная мощность: (ВА, кВА) (16)

где Q = Q_L – Q_C – реактивная мощность цепи.

В данной работе рассматривается электрическая цепь, состоящая из резистора - R, конденсатора - C и катушки индуктивности (r_к, X_L) – (Рис. 4). Катушка обладает не только реактивным сопротивление, но и активным:

r_к = Z_К сos φ_к (17);

X_L = Z_К sin φ_к (18)

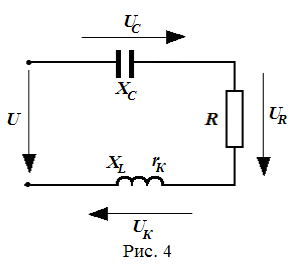
Полное сопротивление катушки Z_К можно найти из закона Ома:

Z_К = (19)

Полное сопротивление цепи Z можно определить:

Z = (20)

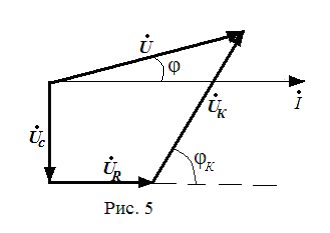
Значение угла сдвига фаз φ_К между падением напряжения на катушке и током взять из предыдущей работы.