Вариант 25 Вариант 26
ξ \ η |
-5 |
10 |
|
||||||
-4 |
|
|
|
||||||
5 |
|
|
|
||||||
8 |
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
ξ \ η |
-12 |
18 |
20 |
5 |
|
|
|
15 |
|
|
|
Вариант 27 Вариант 28
ξ \ η |
1 |
2 |
4 |
|
||||||
-1 |
0,24 |
0,36 |
0,15 |
|
||||||
3 |
0,08 |
0,12 |
0,05 |
|
||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
ξ \ η |
4 |
7 |
9 |
-3 |
0,09 |
0,18 |
0,09 |
2 |
0,16 |
0,32 |
0,16 |
Вариант 29 Вариант 30
ξ \ η |
-4 |
8 |
10 |
||||||
-2 |
|
|
|
||||||
3 |
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
ξ \ η |
1 |
6 |
-3 |
|
|
3 |
|
|
4 |
0,21 |
0,04 |
Задача 3.1.2.
Вычислить математическое ожидание Мθ и дисперсию Dθ случайной величины θ двумя способами: на основании свойств математического ожидания и дисперсии и непосредственно – по ряду распределения θ.
Θ = αξ + β η,
Где ξ, η – дискретные случайные величины из п. 3.1.1. N – номер варианта, α = N – 30, β = N.
Задача 3.3.
Случайный вектор (ξ,η) распределен равномерно в области G, изображенной на рис.3.3.
Найти плотность распределения вероятностей компонент случайного вектора и решить вопрос об их зависимости или независимости.
Выяснить, коррелированы ли компоненты случайного вектора (ξ,η).
Найти Р{(ξ,η) € D}, где D = {(x,y)│ x2 + y2 ≤ 1}.
вар. 1, 16 вар. 2, 17
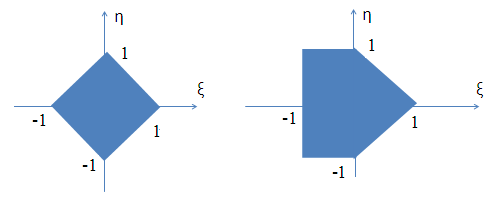
вар. 3, 18 вар. 4, 19
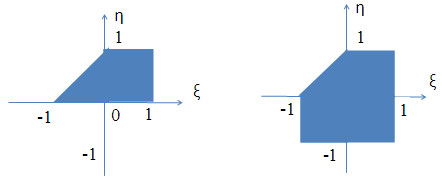
вар. 5, 20 вар. 6, 21
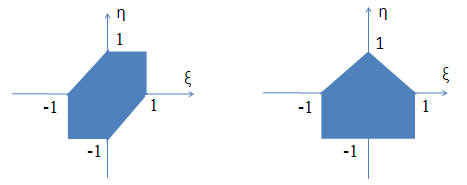
вар. 7, 22 вар. 8, 23
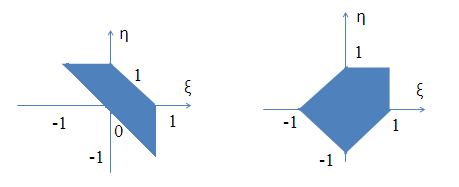
вар. 9, 24 вар. 10, 25
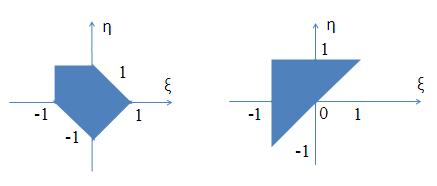
вар 11, 26 вар. 12, 27
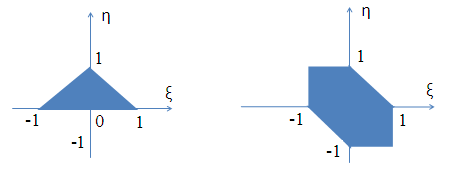
вар. 13, 28 вар. 14, 29 № 15, 30