2.5 Мостовые схемы переменного тока для измерения емкости и угла потерь. Вывод условий равновесия. Особенности.

2.5.1 Измерение емкости и угла потерь конденсатора с малыми потерями.

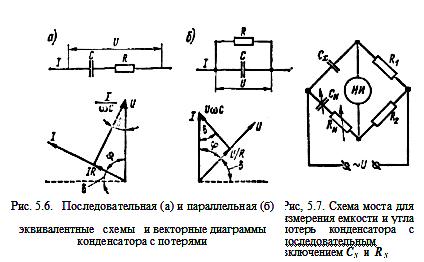
При измерении емкости конденсатора следует учесть, что он обычно обладает потерями, т. е. в нем поглощается активная мощность. Реальный конденсатор представляется эквивалентной схемой в виде идеальной емкости, последовательно или параллельно соединенной с активным сопротивлением, обусловливающим возникновение эквивалентных потерь. Ток в цепи такого конденсатора опережает напряжение на угол, меньший 90°.

; ;

;

Подставив эти выражения в формулу равновесия моста получим

П олучаем уравнение равновесия моста

угол потерь δ , дополняющий до 90° угол сдвига тока относи­тельно напряжения U, определяется из выражения :

Работа на этом мосте производится следующим образом. Уста­новив R_N = 0, изменяют отношение плеч R2/R1 до тех пор, пока нуль-индикатор не укажет наименьший ток. После этого переходят к регулировке магазина R_N, добиваясь дальнейшего уменьшения тока в нуль-индикаторе. Затем снова изменяют отношение R2/R1, пока не будет найдено положение равновесия.

2.5.2 Измерение емкости и угла потерь конденсатора с большими потерями

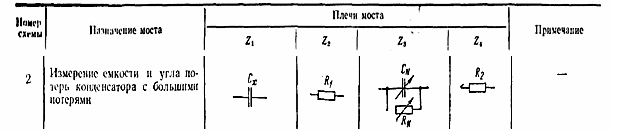
Для измерения емкости конденсаторов

с большими потерями применяется мост с параллельным включением сопротивления R_N и емкости

С_N так как введение последовательно в плечо большого сопротивления уменьшает чувствительность схемы. Комплексные сопротивления плеч моста Z2=R1; Z4=R2 При равновесии имеет место следующее соотношение

Последнее уравнение приводит к двум условиям:

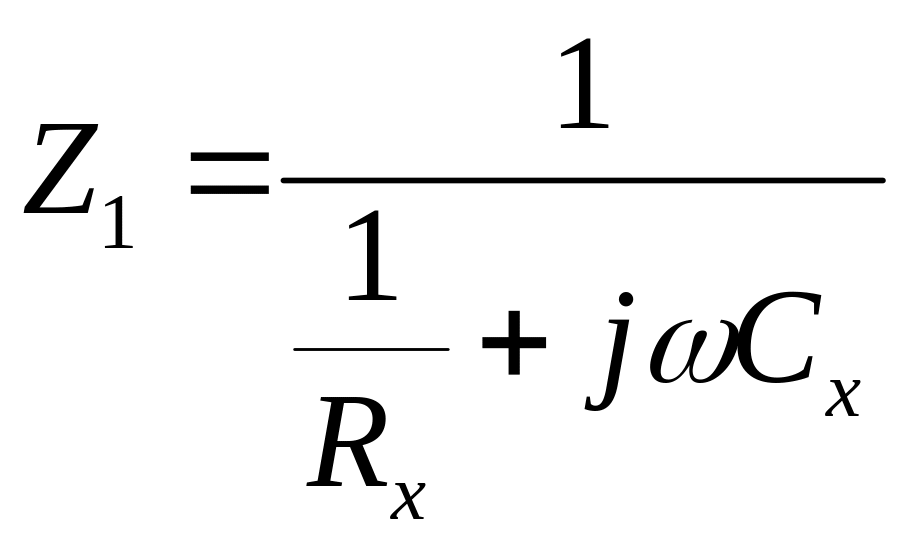
Угол потерь δ для конденсатора С_х, выраженный через tg δ, при параллельном соединении конденсатора и резистора равен:

2.6 Нониусный метод измерения времени и сдвига фаз.

Это метод прямого измерения с однократным сравнением выходных величин двух многозначных нерегулируемых мер с различными ступенями, нулевые отметки которых сдвинуты на измеряемую величину.

Пример. Суть метода на примере штангенциркуля.

1-ая шкала – неподвижная часть штангенциркуля.

2-ая шкала подвижная шкала.

– ступень 1-ой шкалы =1 мм.

– ступень 2-ой шкалы.

– число целых значений, мм.

– число ступеней до совпадения отметок на 1-щй и 2-ой шкалах.

выбирается меньше, чем .

(1) , где – система счисления, для штангенциркуля .

С одной стороны .

С другой стороны .

Приравниваем эти два уравнения: .

Из уравнения (1) получаем: .

.

При подстановке: .

Для .

Для ОНМ используем две меры, степени которых отличаются друг от друга.

Преимущество метода:

1. Повышение точности измерений достигается не за счет десятикратного значения , а за счет применения двух нерегулируемых мер.

2. Метод Нониуса применяется для измерения электрических величин, перемещений узлов поворота, напряжений, угла сдвига фаз, и др.

Одна из разновидностей метода Нониуса – метод Растра (две прозрачные линейки):

Используются две меры с близкими степенями (уравнение (1)). Метки наносятся на прозрачные диски (линейки); при взаимном перемещении нулевых отметок наблюдается перемещение тени. Если фотоприемник поместить на неподвижную шкалу, то число пересечений теней площади фотоприемника равно.

, где – измеряемая длина.