
Задание – 1
Произвести расчет провода определенной марки, известной площади поперечного сечения, подвешенной на воздушной трехфазной линии электропередач.
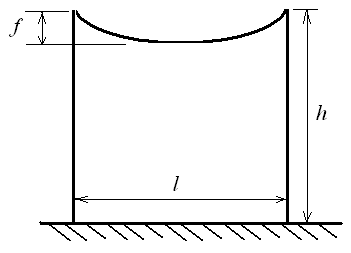
Рисунок. Схема участка ЛЭП
Исходные данные к задаче:
II ветровой район,
q = 400 Па – скоростной напор ветра,
Марка провода – АС,
А
= 24![]() м2
– площадь поперечного сечения провода,
м2
– площадь поперечного сечения провода,
d
= 21,6![]() м – расчетный диаметр провода,
м – расчетный диаметр провода,
qп = 9,97 Н/м – расчетный вес провода,
l = 240 м – пролет между опорами.
tcp.= 10 0C – среднегодовая температура,
tmin = -20 0C – минимальная годовая температура,
tmax = 30 0C – максимальная годовая температура,
Е
= 8,45
![]() Па
– модуль упругости провода,
Па
– модуль упругости провода,
![]() 12,2
12,2![]() Па – допускаемое напряжение,
Па – допускаемое напряжение,
![]() 18,9
18,9![]() – коэффициент линейного расширения
провода.
– коэффициент линейного расширения
провода.
I снеговой район,
![]() 5
м
– толщина стенки гололеда,
5
м
– толщина стенки гололеда,
Решение:
1. Определение удельных приведенных нагрузок при различных режимах работы
1.1. I расчетный режим: провода и тросы покрыты гололедом, t=-5 0C, скоростной напор ветра 0,25q.
Определим вес 1 п.м. гололеда по формуле:
![]()
где
![]() - объемный вес льда, тогда
- объемный вес льда, тогда
![]() 5
5
![]() (21,6+5)
= 3,759 Н/м,
(21,6+5)
= 3,759 Н/м,
Давление ветра на 1 м провода, покрытого гололедом, определим по формуле:
![]() ,
,
где
![]() - коэффициент, учитывающий неравномерность
ветра,
- коэффициент, учитывающий неравномерность
ветра,
К = 1,2 – коэффициент лобового сопротивления, тогда
![]() 400
(21,6
+ 2 .
5)
= 3,192 Н/м.
400
(21,6
+ 2 .
5)
= 3,192 Н/м.
Суммарную интенсивность нагрузки на гибкую нить определим по формуле:
![]()
![]() 14,095 Н/м.
14,095 Н/м.
Удельную нагрузку
определим по формуле:
![]() ,
тогда
,
тогда
![]() .
.
1.2. II расчетный режим: провода и тросы покрыты гололедом, t=-5 0C, ветра нет.
Проводя вычисления, аналогичные п. 1.1. и учитывая, что ветровая нагрузка отсутствует (qв2 = 0), получим:
![]() 3,759
Н/м,
3,759
Н/м,
![]() 13,729
Н/м,
13,729
Н/м,
![]() .
.
1.3. III расчетный режим: скоростной напор ветра q, t=-5 0C.
Гололеда нет (qл = 0). Ветровую нагрузку тогда определим по формуле:
![]()
где
![]() ,
тогда
,
тогда
![]() 400
21,6
= 8,813 Н/м.
400
21,6
= 8,813 Н/м.
![]() Н/м,
Н/м,
![]() .
.
1.4. IV-VII расчетные режимы имеют одинаковую интенсивность нагрузки, ветра и гололеда нет.
![]() 9,97
Н/м, тогда
9,97
Н/м, тогда
![]() .
.
2. Расчет напряжений в проводах
Определим критическую длину пролета по формуле:
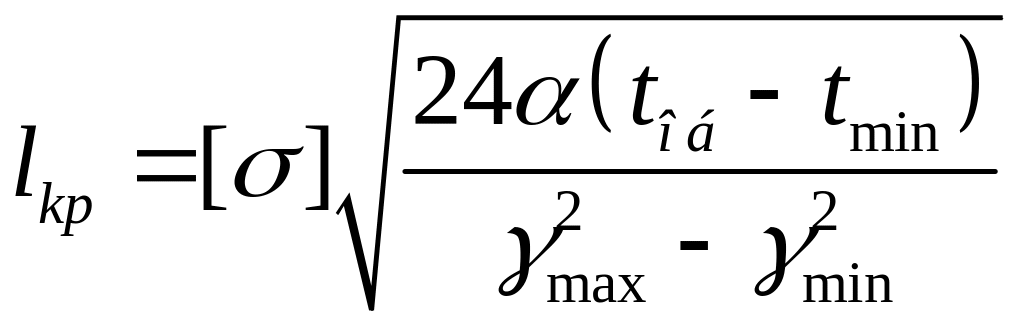 ,
,
где
![]() - температура обледенения,
- температура обледенения,
![]() -
максимальная удельная нагрузка,
соответствующая температуре обледенения
(I
режим),
-
максимальная удельная нагрузка,
соответствующая температуре обледенения
(I
режим),
![]() -
минимальная удельная нагрузка,
соответствующая максимальной годовой
температуре (VI
режим).
-
минимальная удельная нагрузка,
соответствующая максимальной годовой
температуре (VI
режим).
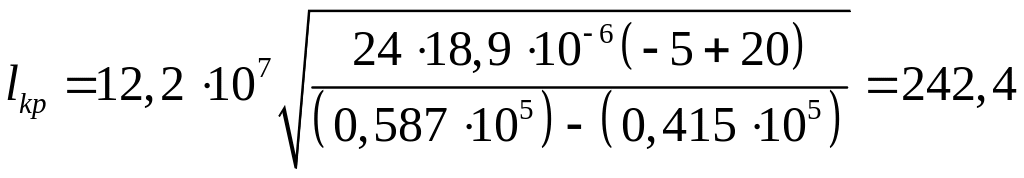 м.
м.
l
= 240 м <
![]() 242,2 м, следовательно, за базовый режим
выбираем VI
с минимальной годовой температурой.
Принимаем
242,2 м, следовательно, за базовый режим
выбираем VI
с минимальной годовой температурой.
Принимаем
![]() = 12,2
Па= = 1,22
= 12,2
Па= = 1,22![]() Па.
Для определения напряжений в других
режимах применим уравнение состояния
нити [2, стр. 30]:
Па.
Для определения напряжений в других
режимах применим уравнение состояния
нити [2, стр. 30]:
Для 7 режима:
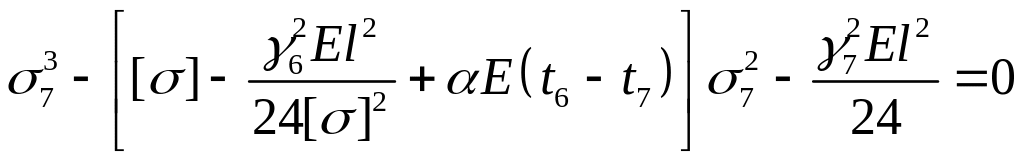 или
или
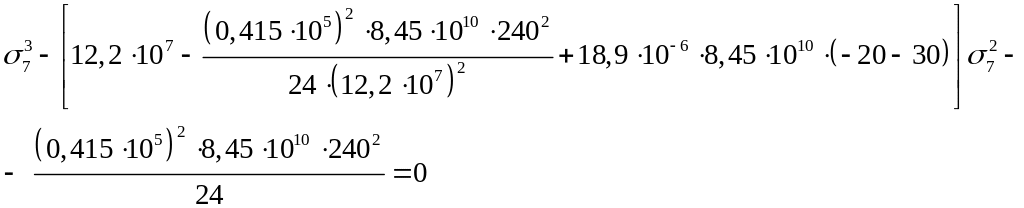
Или после
преобразований:
![]() –0,186
–0,186![]() –3,5
–3,5![]() .
.
Для решения данного
кубического уравнения воспользуемся
известными математическими программами,
основанными на методе Ньютона или
формуле Кардано [3]. Т.к. кубическое
уравнение - это уравнение третьей
степени, то оно имеет три решения:
![]() .
.
Для данного уравнения получаем следующие решения:
![]() 1,583
Па,
остальные 2 корня имеют мнимую
составляющую (i),
поэтому их не рассматриваем. Окончательно
принимаем
1,583
Па,
остальные 2 корня имеют мнимую
составляющую (i),
поэтому их не рассматриваем. Окончательно
принимаем
![]() 1,583
Па.
1,583
Па.
Аналогично для остальных режимов, составляя и решая уравнения состояния нити, получим следующие значения напряжений:
Для 1 режима:
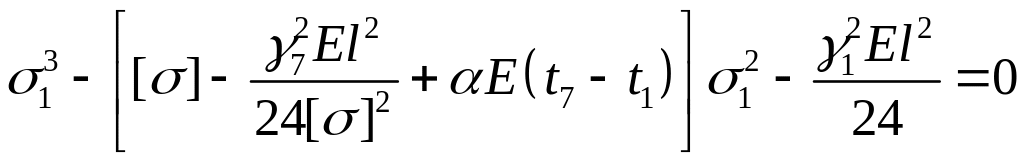 или
или
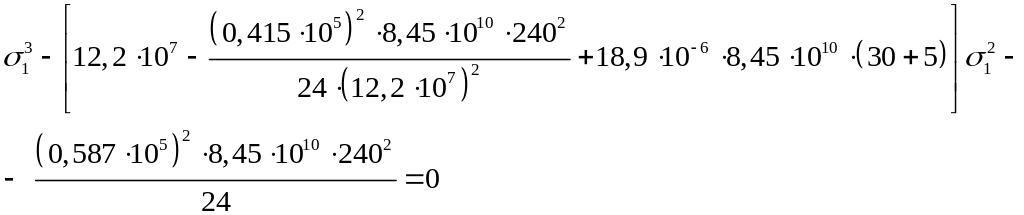
Или после
преобразований:
![]() –1,544
–1,544![]() –6,995
,
–6,995
,
откуда
![]() 1,965
Па.
1,965
Па.
Для 2 режима:
после преобразований:
![]() –0,75
–0,75![]() –6,636
,
–6,636
,
откуда
![]() 2,165
Па.
2,165
Па.
Для 3 режима:
![]() –0,744
–0,744![]() –6,234
,
откуда
–6,234
,
откуда
![]() 2,125
Па.
2,125
Па.
Для 4 режима:
![]() –0,562
–0,562![]() –3,5
,
откуда
–3,5
,
откуда
![]() 1,73
Па.
1,73
Па.
Для 5 режима:
![]() –0,905
–0,905![]() –3,5
,
откуда
–3,5
,
откуда
![]() 1,887
Па.
1,887
Па.
3. Расчет стрелы провисания
Произведем по
формуле:
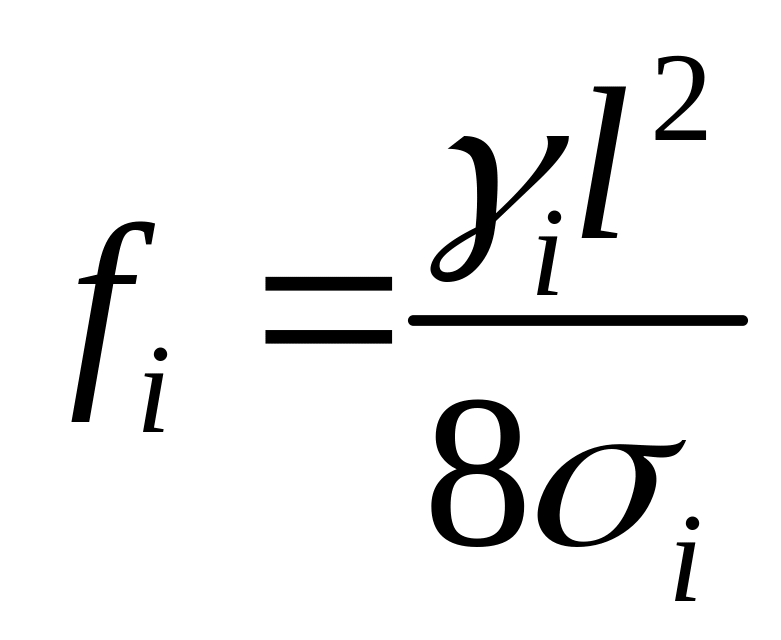 ,
где i
= 1,2,3…7 –
номер режима.
,
где i
= 1,2,3…7 –
номер режима.
Тогда для 1 режима:
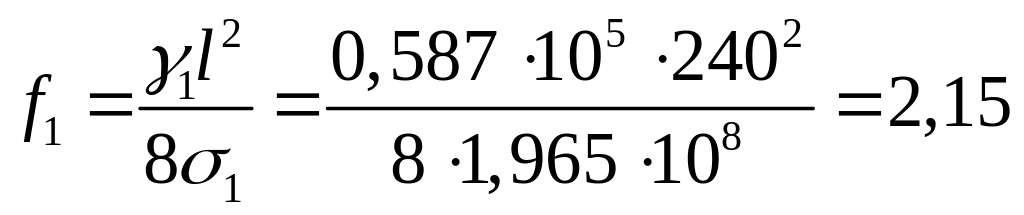 м. Аналогично для остальных режимов:
м. Аналогично для остальных режимов:
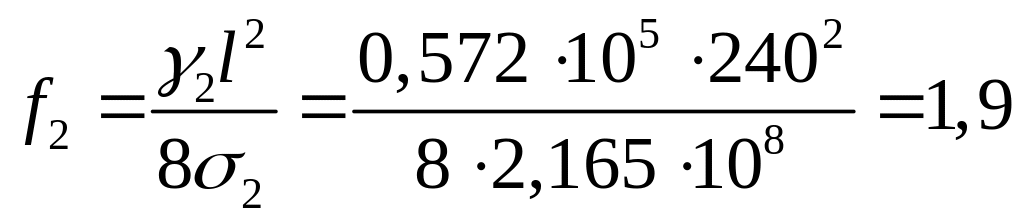 м,
м,
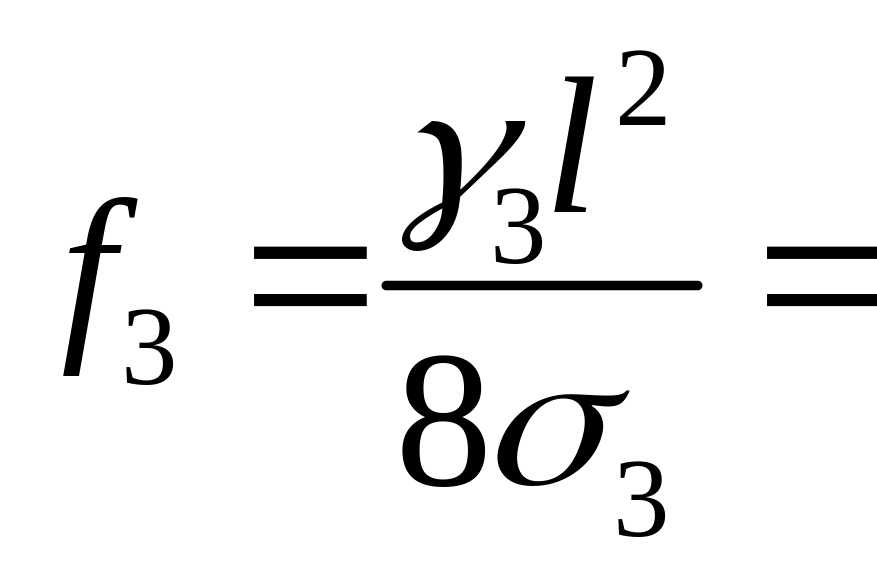 1,88
м,
1,88
м,
![]() 1,73
м,
1,73
м,
![]() 1,59
м,
1,59
м,
![]() 2,45
м,
2,45
м,
![]() 1,89
м.
1,89
м.
В данном варианте
![]() f6
= 2,45 м.
f6
= 2,45 м.
4. Подбор высоты опоры
Высота опоры над землей определяется из условия:
![]()
Тогда в нашем
случае:
![]() 2,45+5,5
= 7,95 м. Принимаем h
= 8 м.
2,45+5,5
= 7,95 м. Принимаем h
= 8 м.
Задание-2
Для заданной схемы балки определить опорные реакции, написать выражения Q и М для каждого участка в общем виде, построить эпюры Q и М, найти Мmаx и подобрать: стальную балку двутаврового поперечного сечения и сечения, составленного из двух швеллеров при [σ] = 160 МПа.
Дано: Схема № 20; а = 1 м, М = 20 кНм, М1 = 15 кНм,
Р = 10 кН, Р1 = 20 кН, q = 20 kH/м, q1 = 15 kH/м.
Решение:
1. Для построения эпюр Q и М необходимо определить опорные реакции из уравнений статики:
![]() 10
. 0,25
– 15 . 4
. 2
– 20 +5 .
4,33
+ RB.4
= 0, RВ
= 28,96 kH,
10
. 0,25
– 15 . 4
. 2
– 20 +5 .
4,33
+ RB.4
= 0, RВ
= 28,96 kH,
![]() 5
.
0,33 + 15 .
8 – 20 + 10 .
4,25 - RA
.
4 =
0, RА
= 36,04 kH,
5
.
0,33 + 15 .
8 – 20 + 10 .
4,25 - RA
.
4 =
0, RА
= 36,04 kH,
Проверка:
![]() -10 + 36,04 – 60 + 28,96 + 5 = 0.
-10 + 36,04 – 60 + 28,96 + 5 = 0.
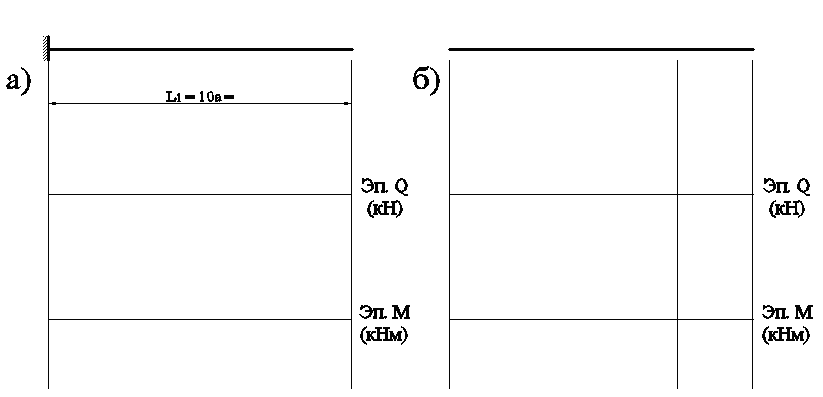
Разбивая балку на грузовые участки, проводя сечение и отбрасывая более сложную часть, составим уравнения равновесия поперечных сил Q и изгибающих моментов М для участков.
Участок I
![]() 0,25
м
0,25
м
![]()
![]() -10
= 0
-10
= 0
![]() -10
кН = const.
-10
кН = const.
![]() ;
;
![]() +10х1
= 0
+10х1
= 0
= -10 х1
![]()
![]()
Участок
II
0,25![]() 2,25 м
2,25 м
![]() -10+36,04-15(х2-0,25)
= 0
-10+36,04-15(х2-0,25)
= 0
![]() 26,04-15(х2-0,25)
26,04-15(х2-0,25)
;
![]() +15(х2-0,25)2/2+10х2-36,04(х2-0,25)
= 0
+15(х2-0,25)2/2+10х2-36,04(х2-0,25)
= 0
= 36,04(х2-0,25)- 10х2-7,5(х2-0,25)2
![]()
![]()
Участок III
0
![]() 0,33 м
0,33 м
![]() +5
= 0
+5
= 0
![]() -5
= const.
-5
= const.
;
![]() -5х3
= 0
-5х3
= 0
= 5х3
![]()
![]()
По полученным значениям строим эпюры внутренних силовых факторов Q и М (см. рисунок).
2. Подбор размеров
поперечного сечения двутавровой балки.
Условие прочности при изгибе запишем:
![]() ,
где
,
где
![]() – максимальный
изгибающий момент, возникающий в балке,
– максимальный
изгибающий момент, возникающий в балке,
Wх – момент сопротивления поперечного сечения балки.
Тогда
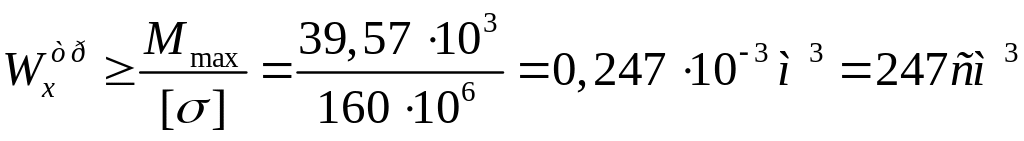 .
.
– сечение,
составленное из 2-х швеллеров:
![]() 123,5 см3.
По сортаменту швеллеров (ГОСТ 8240-89)
принимаем швеллер № 18а с
123,5 см3.
По сортаменту швеллеров (ГОСТ 8240-89)
принимаем швеллер № 18а с
![]() =
132 см3
и А[
= 22,2 см2.
Тогда общая площадь А = 2А[
= 44,4 см2.
=
132 см3
и А[
= 22,2 см2.
Тогда общая площадь А = 2А[
= 44,4 см2.
– двутавровое
сечение:
![]() .
По сортаменту двутавров (ГОСТ 8239-89)
принимаем двутавр № 22а с
= 254 см3;
А = 32,8 см2;
.
По сортаменту двутавров (ГОСТ 8239-89)
принимаем двутавр № 22а с
= 254 см3;
А = 32,8 см2;
Сравнивая площади подобранных сечений, приходим к выводу, что наиболее выгодным по расходу материала является двутавровое сечение с минимальной площадью.
Задание 3
Определить диаметры
валов сплошного и полого с отношением
внутреннего диаметра к наружного
![]() .
Установить разницу в расходе материала,
проверить жесткость валов. Построить
эпюру углов закручивания
.
Установить разницу в расходе материала,
проверить жесткость валов. Построить
эпюру углов закручивания
![]() для рационального сечения, эпюру
касательных напряжений
для рационального сечения, эпюру
касательных напряжений
![]() для сечений, удовлетворяющих условиям
прочности и жесткости.
для сечений, удовлетворяющих условиям
прочности и жесткости.
Дано: n = 500 об/мин, Р1 = 90 кВт, Р2 = 80 кВт, Р3 = 60 кВт, Р4 = 50 кВт,
а =
0,1 м, с =
0,3 м,
![]() ,
,
![]() ,
,
![]() .
.
=
0,75,
![]() 2.
2.
Решение
1. Определим величины внешних вращающих моментов по формуле:
М =
![]()
![]() кНм,
кНм,
![]() кНм, аналогично
кНм, аналогично
М3 = 1,15 кНм, М4 = 0,96 кНм.
При равномерном вращении вала алгебраическая сумма внешних моментов равна нулю: М2 + М3 – М1 – М5 – М4 = 0, тогда М5 = 0.
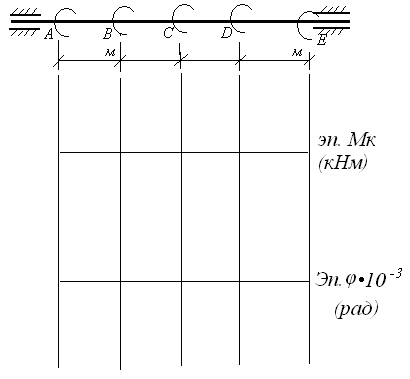
По этим значениям строим эпюру крутящих моментов Мкр. (см. чертеж).
2. Определим диаметр круглого вала из условий прочности при кручении:
![]() 90
МПа, где
90
МПа, где
![]() - полярный момент
сопротивления поперечного сечения вала
(круга). Тогда
- полярный момент
сопротивления поперечного сечения вала
(круга). Тогда
![]() .
Отсюда найдем диаметр вала:
.
Отсюда найдем диаметр вала:
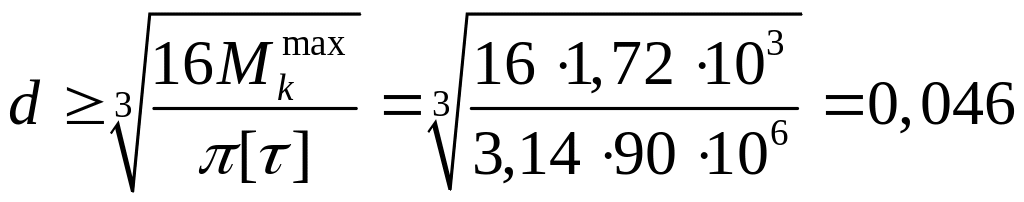 м = 46 мм.
м = 46 мм.
Принимаем по ГОСТ 2590-71 d = 46 мм.
Кольцевого
поперечного сечения:
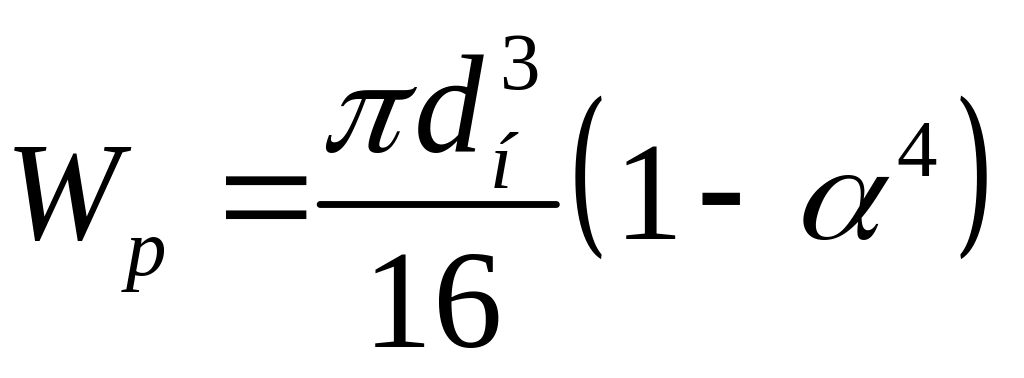 ,
где
,
где
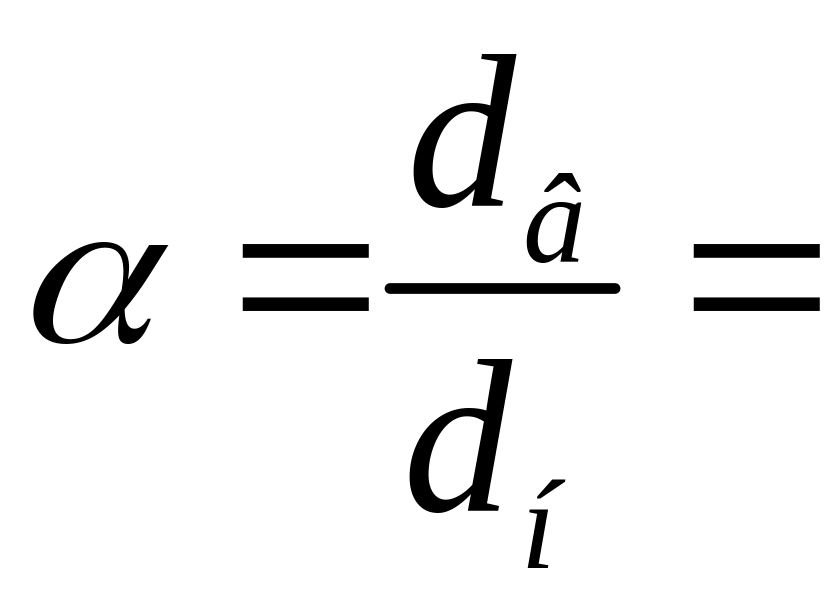 0,75,
тогда
0,75,
тогда
 м = 52 мм.
м = 52 мм.
Принимаем по ГОСТ
2590-71 dн
= 53 мм, тогда dв
=
![]() 40
мм.
40
мм.
3. Определим диаметр круглого вала из условий жесткости при кручении.
Условие жесткости при кручении имеет вид:
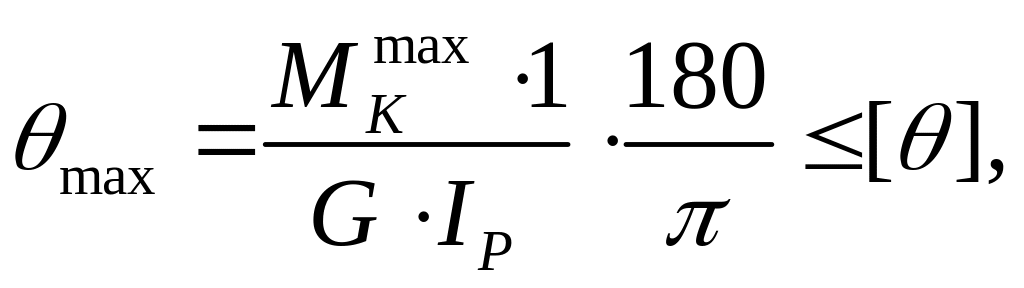 где
где
![]() - угол закручивания
на один погонный метр,
- угол закручивания
на один погонный метр,
![]() - максимальный
крутящий момент,
- максимальный
крутящий момент,
![]() - жёсткость при
кручении (
),
- жёсткость при
кручении (
),
![]() - допускаемый угол
закручивания на 1 п.м.,
.
- допускаемый угол
закручивания на 1 п.м.,
.
Для сплошного
вала:
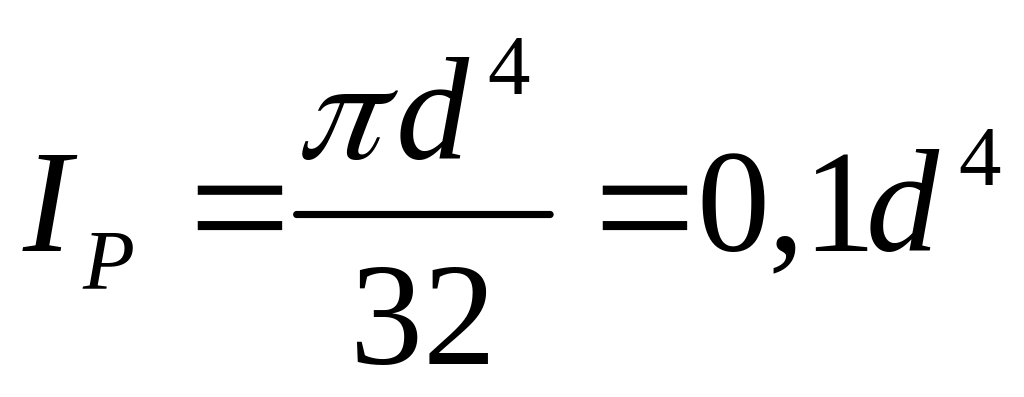 ,
,
Тогда найдем
диаметр вала из условия жёсткости:
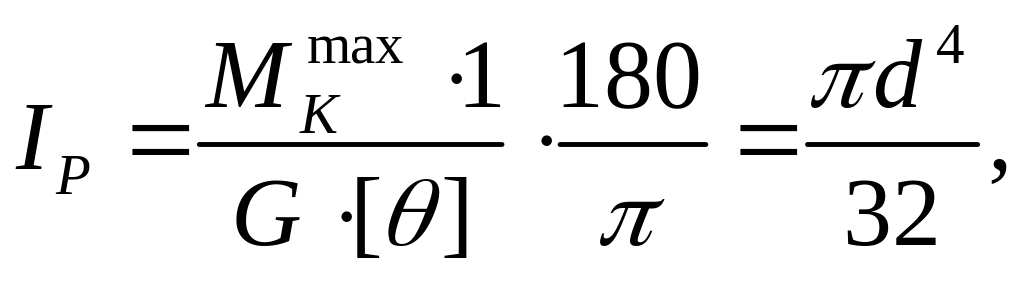
отсюда
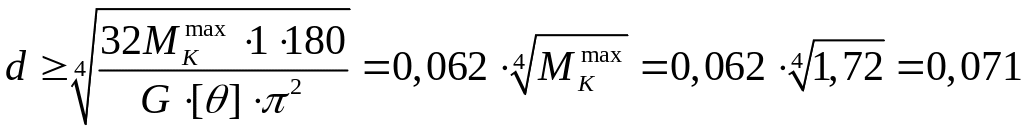 м = 71 мм.
м = 71 мм.
Принимаем по ГОСТ 2590-71 d = 75 мм.
Для пустотелого
вала:
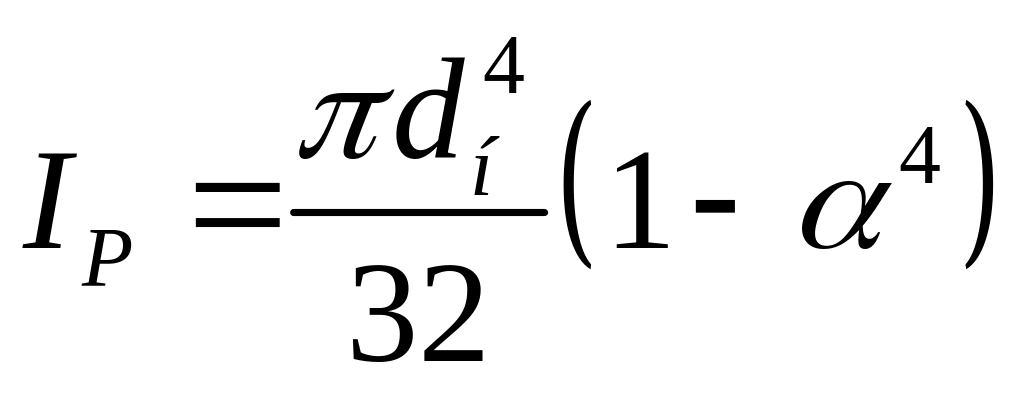 .
Найдем диаметр вала из условия жёсткости:
.
Найдем диаметр вала из условия жёсткости:
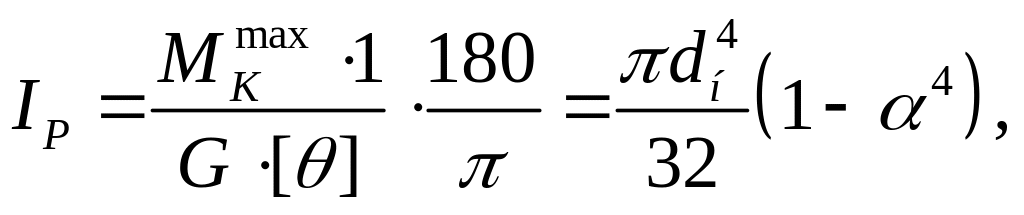 отсюда
отсюда
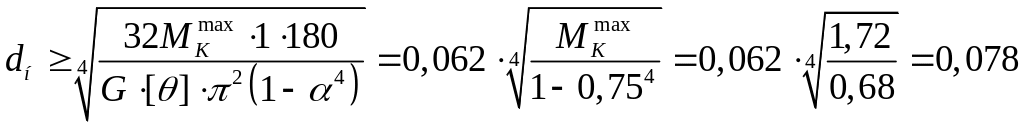 м = 78 мм.
м = 78 мм.
Принимаем по ГОСТ 2590-71 dн = 80 мм, тогда dв = 60 мм.
Для обеспечения прочности и жесткости вала принимаем сечения большего диаметра: d = 75 мм. Для пустотелого вала: dн = 80 мм, dв = 60 мм. Площади поперечного сечения данных валов будут равны соответственно:
![]() мм2,
мм2,
![]() мм2.
мм2.
Окончательно принимаем вал кольцевого поперечного сечения с минимальной площадью, что выгоднее с точки зрения расхода материала при одинаковой нагрузке.
4. Построим эпюру углов закручивания. Для этого определим углы поворота сечений относительно начало отсчета, за которое примем крайнюю левую точку вала – А.
Жесткость вала:
=
![]() Нм2
Нм2
Угол поворота сечения В относительно сечения А равен
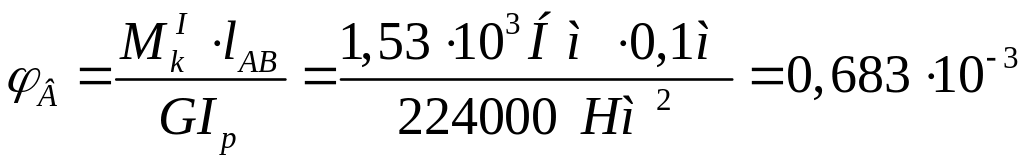 рад;
рад;
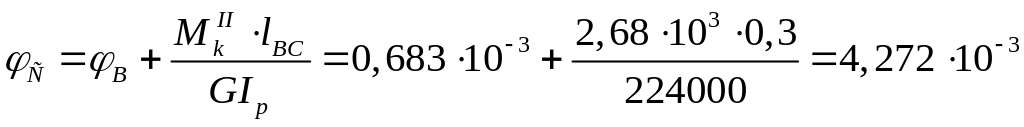 рад;
рад;
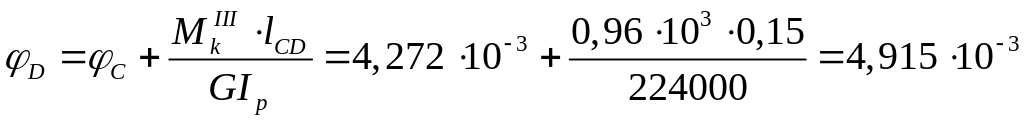 рад,
рад,
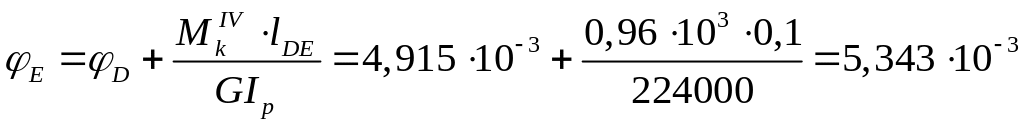 рад.
рад.
По полученным данным строим эпюру углов закручивания φ (см. чертеж).
5. Построим эпюры распределения касательных напряжений для сечений, удовлетворяющим условиям прочности и жесткости.
Круглое поперечное сечение: d = 75 мм.
=
![]() (75
м)3
= 0,084
м3
(75
м)3
= 0,084
м3
 МПа.
МПа.
Кольцевое поперечное сечение: dн = 80 мм, 0,75
![]()
![]() (80
м)3
(80
м)3![]() =
0,070
м3
=
0,070
м3
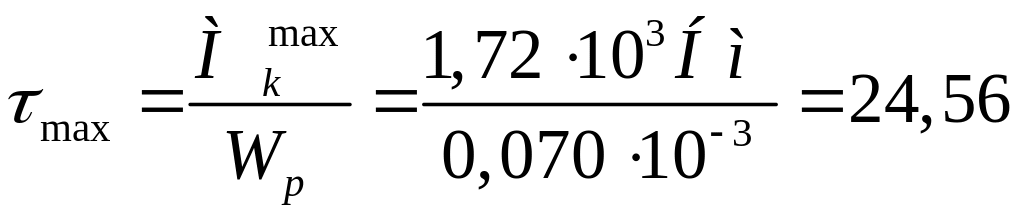 МПа.
МПа.
![]() (80
м)4
=
2,8
(80
м)4
=
2,8![]() м3
м3
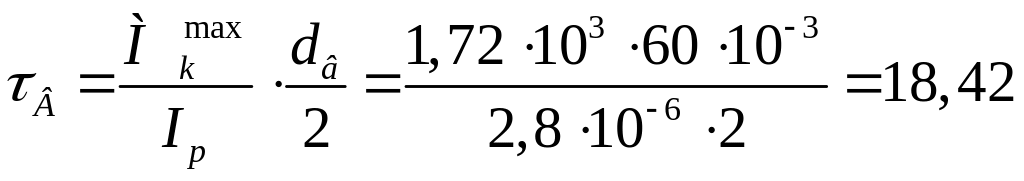 МПа.
МПа.

Рисунок. Эпюры распределения касательных напряжений
Задание 4.
Стержень указанного материала длиной l сжимается силой F. Требуется: 1) найти размеры поперечного сечения при допускаемом напряжении на простое сжатие, 2) найти значение критической силы и коэффициент запаса устойчивости.
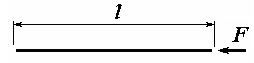
ДАНО: Стержень длиной
![]() 3 м,
3 м,
![]() 100 кН,
100 кН,
μ = 0,7
Материал стойки сталь марки Ст3.
Расчетное сопротивление
стали
![]() МПа,
МПа,
Предельное значение гибкости
![]() .
.
Решение:
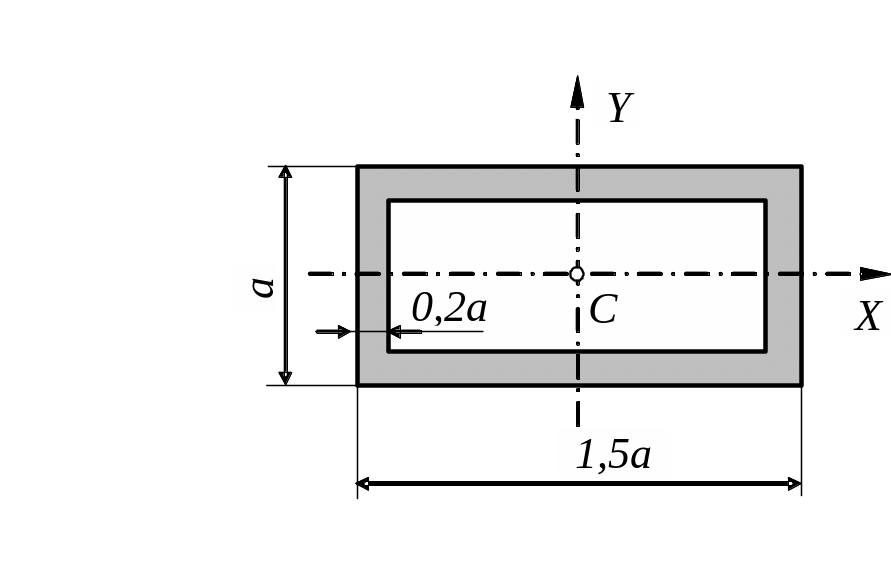
1. Определение геометрических характеристик сечения стержня.
Сечение
разбиваем на два элемента: первый элемент
– прямоугольник с размерами
![]() ;
второй элемент – вырезанный прямоугольник
с размерами
;
второй элемент – вырезанный прямоугольник
с размерами
![]() .
.
Суммарная площадь составного сечения равна:
![]() .
.
Находим
минимальный осевой момент инерции
заданного поперечного сечения стержня:
![]() .
.
Определяем величину минимального радиуса инерции сечения:
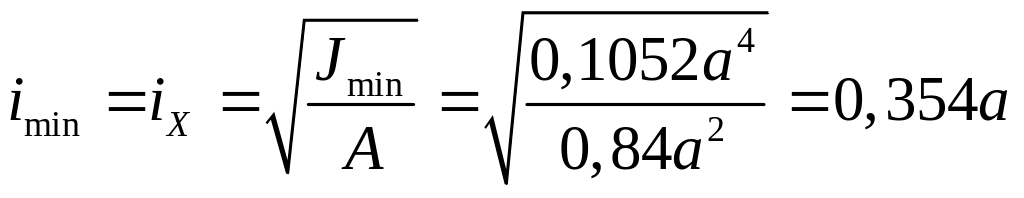 .
.
2. Определение размеров поперечного сечения стержня методом последовательных приближений.
Условие устойчивости сжатого стержня:
![]()
Задаемся начальным приближением
коэффициента продольного изгиба
![]() .
Тогда из условия устойчивости определяем
требуемую площадь поперечного сечения
стержня:
.
Тогда из условия устойчивости определяем
требуемую площадь поперечного сечения
стержня:
![]() см2.
см2.
Учитывая ранее полученные выражения
для величин
![]() и
и
![]() ,
имеем:
,
имеем:
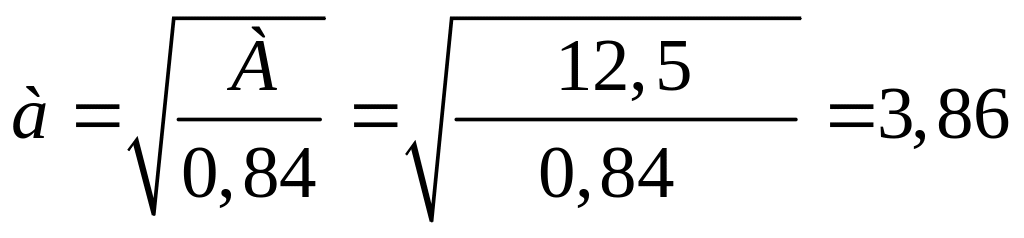 см;
см;
![]() см.
см.
Вычисляем гибкость стержня по формуле:
![]()
где
![]()
коэффициент приведенной длины, выбираемый
в зависимости от условий закрепления
концов стержня.
коэффициент приведенной длины, выбираемый
в зависимости от условий закрепления
концов стержня.
По
таблице
![]()
![]() с помощью линейной интерполяции находим
значение коэффициента продольного
изгиба соответствующее вычисленному
значению гибкости :
с помощью линейной интерполяции находим
значение коэффициента продольного
изгиба соответствующее вычисленному
значению гибкости :
![]()
Полученное значение коэффициента отличается от ранее принятого, следовательно, необходимо выполнить следующее приближение.
Второе приближение. Задаемся новым
значением коэффициента продольного
изгиба:
![]() .
.
![]() см2.
см2.
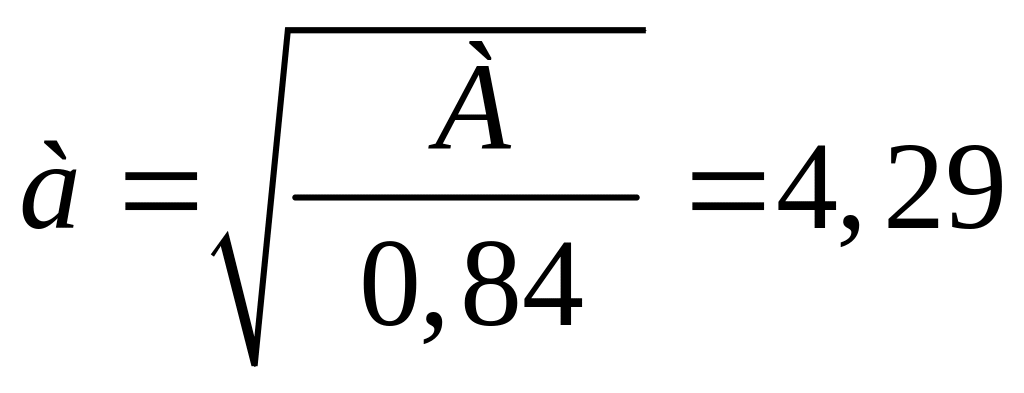 см;
см;
![]() см,
см,
![]()
![]()
Третье приближение.
![]() .
.
![]() см2,
см2,
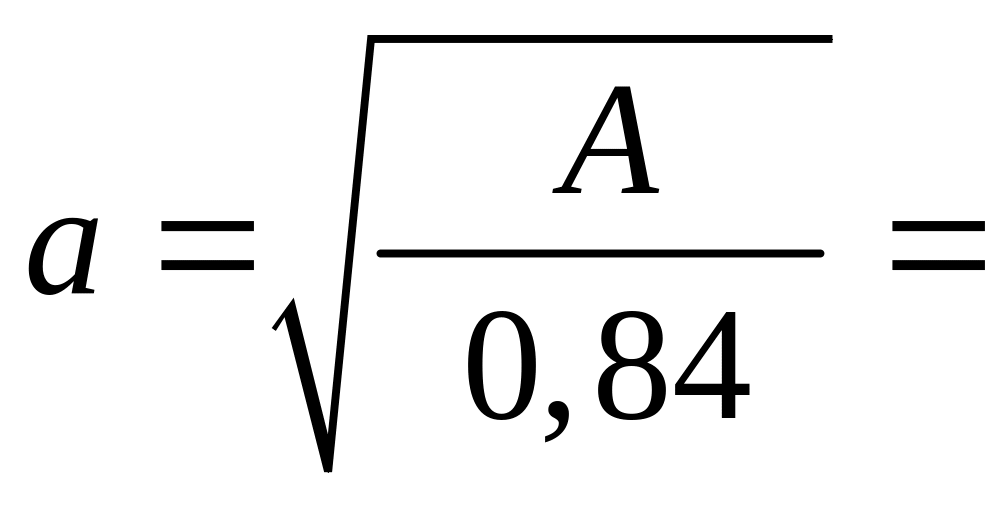 4,39 см;
4,39 см;
![]() см,
см,
![]()
![]()
Находим значение расчетных напряжений в сечении сжатого стержня:
![]() МПа >
МПа >
![]() МПа.
МПа.
![]() ,
что допустимо.
,
что допустимо.
3. Определение величины критической силы:
Расчетная гибкость стойки
![]() (предельное значение гибкости),
следовательно, при определении критических
напряжений необходимо использовать
формулу
(предельное значение гибкости),
следовательно, при определении критических
напряжений необходимо использовать
формулу
Эйлера :
![]()
![]() МПа
МПа
![]() 108,01
108,01![]() 16,19
16,19
![]() =
174 КН.
=
174 КН.
Коэффициент запаса устойчивости:
![]() .
.
Литература:
1. Методические указания по сопротивлению материалов для студентов спец. 310900 - «Землеустройство», 311000 - «Земельный кадастр», 311400 – «Электрификация и автоматизация с/х процессов», КубГАУ, Краснодар, 2005.
2. Бредихин Б.А. Сопротивление материалов. Краснодар, КГАУ, 2006 г.
3. http://cubic-solver.info/calc.php - программа для решения кубических уравнений.
4. Александров А.В. Сопротивление материалов.
5. Писаренко. Справочник по сопротивлению материалов.
