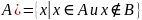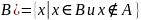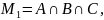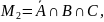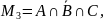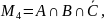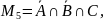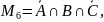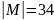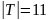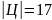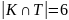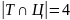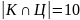- •Федеральное агентство по образованию новосибирский государственный университет экономики и управления – «нинх»
- •Тексты лекций учебной дисциплины «Математика и информатика (математика)»
- •Математика
- •Введение в математику
- •Введение в теорию множеств
- •Начальные сведения о множествах
- •Способы задания множеств
- •Операции над множествами
- •Свойства операций над множествами
- •Разбиение множества на классы
- •Основы линейной алгебры
- •Определение матрицы
- •Определители второго и третьего порядков, их основные свойства
- •Миноры и их алгебраические дополнения, разложение определителя по строке (столбцу)
- •Свойства определителей
- •Операции над матрицами, их свойства
- •Свойства операций над матрицами
- •Обратная матрица и ее вычисление
- •Системы линейных уравнений
- •Матричный метод решения систем линейных уравнений
- •Правило Крамера
- •Метод Гаусса
- •Решение слу с использованием табличного процессора ms Excel
- •Функции рабочего листа для работы с матрицами
- •Решение систем линейных уравнений матричным методом
- •Решение систем линейных уравнений методом Крамера
- •Пошаговое решение системы линейных уравнений методом Гаусса
- •Математические модели
- •Основные понятия
- •Построение математических моделей простейших задач оптимизации
- •Графический метод решения задач линейного программирования
- •Технология решения задач линейного программирования с помощью Поиска решений в среде excel
- •1. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
- •2. Ввести исходные данные.
- •3. Ввести зависимость для целевой функции
- •4. Ввести зависимости для ограничений.
- •5. Назначить целевую функцию (установить целевую ячейку), указать адреса изменяемых ячеек.
- •6. Ввести ограничения
- •7. Ввести параметры для решения злп
- •Теория вероятностей
- •Элементы комбинаторики
- •Случайные события и их вероятности
- •Случайные события
- •Операции над событиями
- •Определение вероятности события
- •Теоремы сложения и умножения вероятностей
- •Формула полной вероятности. Формула Байеса
- •Повторные независимые испытания
- •Случайная величина
- •Основные понятия
- •Распределение частоты пульса в группе из 47 человек
- •Функция распределения
- •Числовые характеристики случайных величин
- •Законы распределения дискретных случайных величин
- •Непрерывные случайные величины
- •Основные законы распределения непрерывных случайных величин
- •Контрольные вопросы
- •Основы математической статистики
- •Задачи математической статистики
- •Генеральная совокупность и выборка
- •Статистическое распределение (вариационный ряд). Гистограмма. Полигон
- •Характеристики положения и рассеяния статистического распределения
Операции над множествами
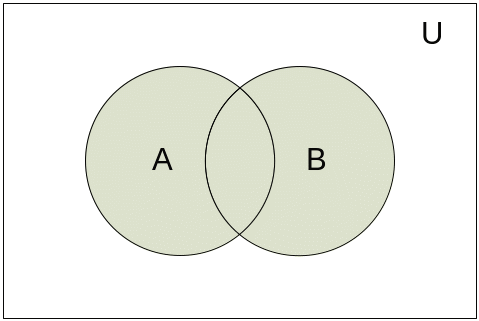
Рассмотрим такие операции над множествами, как объединение, пересечение, разность и дополнение.
Объединением
множеств A
и B
(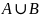 )
называется множество, состоящее из всех
тех элементов, которые принадлежат хотя
бы одному из множеств А или В (рис.
2.2.3.).
)
называется множество, состоящее из всех
тех элементов, которые принадлежат хотя
бы одному из множеств А или В (рис.
2.2.3.).
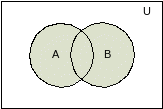
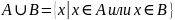
Рис. 2.2.3. Диаграмма Эйлера-Венна для объединения множеств А и В
Пример 2.2.2.
Даны два множества: A
= {1, 2, 4, 6} и В = {0, 3, 4, 6}. Найти множество
 .
С = {0, 1, 2, 3, 4, 6}.
.
С = {0, 1, 2, 3, 4, 6}.
Пересечением
множеств А и В (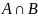 )
называется множество, состоящее из
элементов, входящих как в множество А,
так и в множество В (рис. 2.2.4.).
)
называется множество, состоящее из
элементов, входящих как в множество А,
так и в множество В (рис. 2.2.4.).

Рис. 2.2.4. Диаграмма Эйлера-Венна для пересечения множеств А и В
Пример 2.2.3.
Даны два множества: A
= {1, 2, 4, 6} и В = {0, 3, 4, 6}. Найти множество
 .
С = {4, 6}.
.
С = {4, 6}.
Разностью
множеств А и В (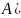 )
называется множество всех элементов
множества А, которые не содержатся в В
(рис. 2.2.5.).
)
называется множество всех элементов
множества А, которые не содержатся в В
(рис. 2.2.5.).
|
|
Рис. 2.2.5. Диаграмма Эйлера-Венна для разности двух множеств
Пример 2.2.4.
Даны два множества: A
= {1, 2, 4, 6} и В = {0, 3, 4, 6}. Найти множество
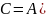 и
и
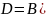 .
С = {1, 2}, D
= {0, 3}.
.
С = {1, 2}, D
= {0, 3}.
Дополнением
(до универсального множества U)
множества A
(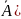 называется множество всех элементов,
не принадлежащих A,
но принадлежащих универсальному
множеству U
(рис. 2.2.6.).
называется множество всех элементов,
не принадлежащих A,
но принадлежащих универсальному
множеству U
(рис. 2.2.6.).
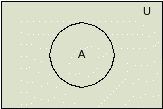
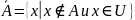
Рис. 2.2.6. Диаграмма Эйлера-Венна для разности двух множеств
Пример 2.2.5.
Пусть универсальное множество U
состоит из букв русского алфавита, A
– множество гласных букв, тогда
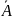 - множество согласных букв и букв ь и ъ.
- множество согласных букв и букв ь и ъ.
Приоритет выполнения операций: сначала выполняются операции дополнения, затем пересечения и только потом объединения и разности. Последовательность выполнения операций может быть изменена скобками.
Пример 2.2.6.
Пусть U
= {1, 2, 3,
4}, А = {1, 3, 4}, В
= {2, 3}, С = {1, 4}.
Найти: а)
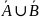 ;
б)
;
б)
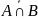 ;
в)
;
в)
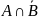 ;
г)
;
г)
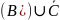 .
.
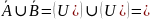 ;
; ;
;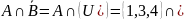 ;
;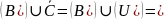 .
.
Свойства операций над множествами
Закон идемпотентности для объединения и пересечения множеств:
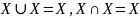 .
.
Закон коммутативности:
 .
.
Закон ассоциативности:
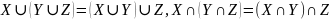 .
.
Законы дистрибутивности:
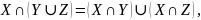
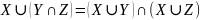 .
.
Законы поглощения:
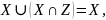
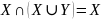 .
.
Законы, описывающие свойства пустого и универсального множеств по отношению к объединению и пересечению:
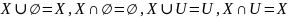 .
.
Законы дополнения:
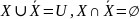 .
.Закон инволютивности дополнения:
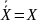 .
.Закон Де Моргана:
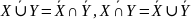 .
.
Разбиение множества на классы
Разбиением множества A на классы Ai называется представление данного множества в виде суммы попарно непересекающихся его подмножеств Ai, i = 1, 2, ..., n, таких, что каждый элемент множества A является в то же время и элементом одного из подмножеств Ai, то есть:
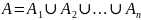 .
.
Пусть
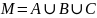 ,
где A, B, C
– пересекающиеся множества. Тогда
разбиение множества M
на классы можно представить в следующем
виде (рис. 2.2.7.):
,
где A, B, C
– пересекающиеся множества. Тогда
разбиение множества M
на классы можно представить в следующем
виде (рис. 2.2.7.):
|
|
Рис. 2.2.7. Диаграмма Эйлера-Венна для разбиения множеств на классы
В общем случае при разбиении на классы множества, состоящего из 3 пересекающихся множеств, получается 7 классов, то есть 7 попарно непересекающихся подмножеств.
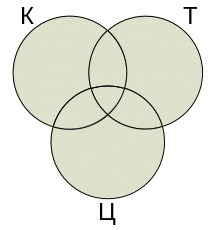
Пример 2.2.7. После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников класса двое не были ни в кино, ни в театре, ни в цирке. В кино побывало 25 человек, в театре – 11, в цирке – 17; и в кино, и в театре – 6; и в кино, и в цирке – 10; и в театре, и в цирке – 4. Сколько человек побывало и в кино, и в театре, и в цирке? Сколько человек посетили только одно мероприятие?
Пусть множество К
– это ученики, посетившие кино, Т –
ученики, посетившие театр, Ц – ученики,
посетившие цирк во время зимних каникул.
Тогда
 .
Мощность множества
.
Мощность множества
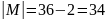 (общее количество учеников за вычетом
тех, кто не был ни в театре, ни в кино, ни
в цирке). Построим диаграмму Эйлера-Венна
и нанесем на неё мощности классов, исходя
из условия. Для наглядности будет
использовано несколько диаграмм (рис.
2.2.8.):
(общее количество учеников за вычетом
тех, кто не был ни в театре, ни в кино, ни
в цирке). Построим диаграмму Эйлера-Венна
и нанесем на неё мощности классов, исходя
из условия. Для наглядности будет
использовано несколько диаграмм (рис.
2.2.8.):
|
||
а) |
б) |
в) |
г) |
д) |
е) |
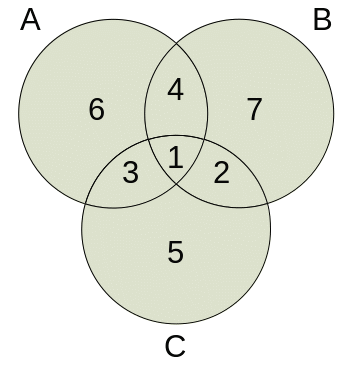
Рис. 2.2.8.
Пусть х – это
количество учеников, которые посетили
все три мероприятия, то есть
 .
.
Тогда количество учеников, посетивших только театр и цирк, без кино, равно:
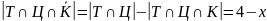 .
.
Аналогично находим количество учеников, посетивших только цирк и кино, за исключением театра:
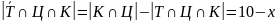 .
.
И, наконец, количество учеников, посетивших только театр и кино, за исключением цирка, равно:
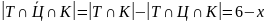 .
.
Рассчитаем мощности оставшихся 3 классов:
количество учеников, посетивших только театр:
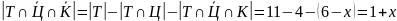 ;
;
количество учеников, посетивших только цирк:
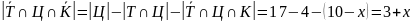 ;
;
количество учеников, посетивших только кино:
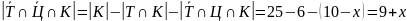 .
.
Нанесем расчетные данные по каждому классу на диаграмму для дальнейших вычислений (рис. 2.2.9.):
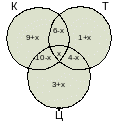
Рис. 2.2.9.
Для ответа на первый
вопрос задачи необходимо найти мощность
класса
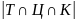 ,
то есть х. Для вычисления x будем
использовать мощность множества
,
то есть х. Для вычисления x будем
использовать мощность множества
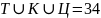 и составим уравнение, просуммировав
мощности всех 7 классов:
и составим уравнение, просуммировав
мощности всех 7 классов:
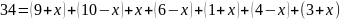 .
.
Следовательно,
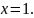 То есть 1 ученик побывал
и в кино, и в театре, и в цирке.
То есть 1 ученик побывал
и в кино, и в театре, и в цирке.
Для ответа на второй вопрос задачи необходимо просуммировать мощности трех внешних классов:
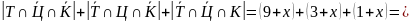
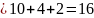 .
.
То есть 16 учеников посетили только одно мероприятие.