ТАУ , 12 вариант , ИИТ заочка

КОНТРОЛЬНАЯ РАБОТА

Исходные данные к контрольной работе

Структурная схема линейной САУ представлена на рис. 1, где соответствующие передаточные функции имеют вид апериодических звеньев:

Рис. 1

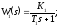
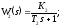
Параметры

Т₁ = 0,05;

Т₂ = 0,6;

Т₃ = 0,1;

К₁ = 14,5;

К₃ = 1,4.

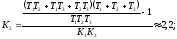
Величина коэффициента К₂ выбирается далее из условия устойчивости.

Решение.

1. Передаточные функции находятся с использованием правил структурных преобразований |1, с. 27 - 34].

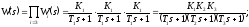
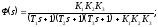
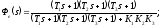
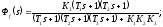
2. Если найдена главная передаточная функция замкнутой системы в ви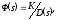де где 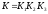- общий коэффициент передачи прямой цепи, D(s) - полином относительно s, то характеристическое уравнение замкнутой системы имеет вид:

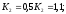
3. Определение частотных характеристик и их построение.

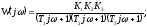
Рис. 2 График АФЧХ

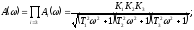
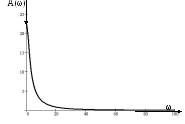
Рис. 3. График АЧХ.

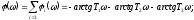
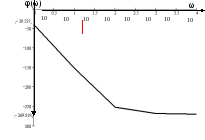
Рис. 4. График АФЧХ

ω

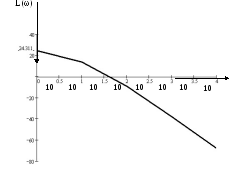
Рис. 5 График ЛАЧХ

4. Статическая ошибка:

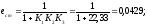
Частота среза системы ω_с определяется но графику ЛАЧХ. Это значение частоты, при котором 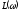пересекает ось абсцисс и где

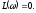
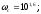
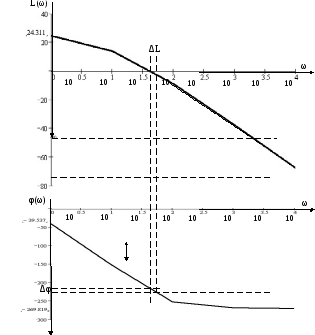
Запасы устойчивости ΔL и Δφ также находятся из логарифмических характеристик.

Рис 6. Запасы устойчивости.

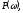
Время регулирования t_р и перерегулирование σ ориентировочно можно оценить, используя максимальное значение Р_max вещественной частотной характеристики 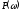и частоту среза системы ω_с.

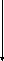
P(ω)

ω

P_max

Рис. 7 График вещественной частотной характеристики

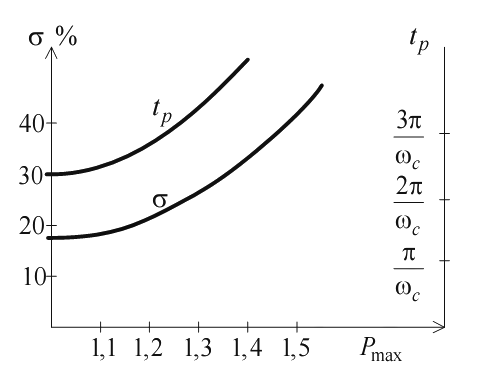
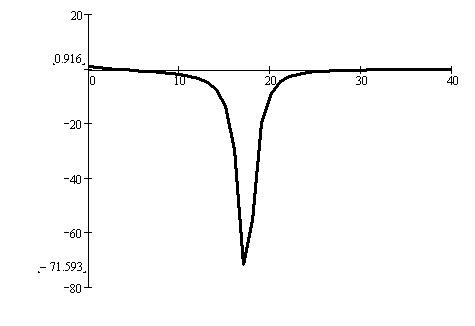
Показатель колебательности определяют из графика амплитудно-частотной характеристики замкнутой системы как .

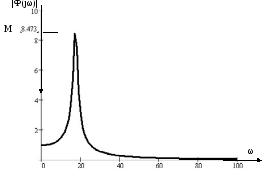
Рис.8 График амплитудно-частотной характеристики замкнутой системы

5. Зная передаточную функцию, связывающую изображения входа и выхода системы, нетрудно получить дифференциальное уравнение, связывающее входную и выходную координаты системы (f = 0):

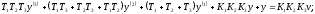
6. По дифференциальному уравнению, полученному в предыдущем пункте, легко найти уравнения состояния в нормальной форме. Коэффициенты:

.

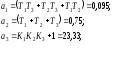
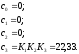
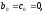
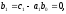
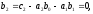
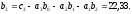
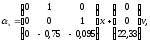
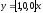7. При принятии решения о замене дискретной системы эквивалентной непрерывной системой необходимо сравнить значение периода дискретизации Т с рядом величин, влияющих на процессы в системе. Эквивалентирование возможно при выполнении ряда условий:

1. 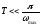, где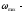 наибольшая частота возмущающих и задающих сигналов. Обычно принимают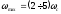

2. 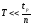., где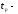- время регулирования, а n - порядок системы.

3. В следящих системах с учетом динамической точности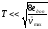, где - заданная ошибка слежения, 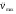- максимальное ускорение входного сигнала.

4. С учетом ухудшения запаса устойчивости 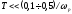, где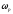 - рабочая частота сигналов в системе.

5. С учетом показателя колебательности

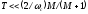
Из всех ограничений выбирают наиболее жёсткое.