Министерство образования Республики Беларусь

Учреждение образования

«Белорусский государственный университет

информатики и радиоэлектроники»

Контрольная работа

по предмету «Телемеханика»

Выполнил: студент 3 курса группы 982421

2011

Контрольная работа № 1

Рассчитать и построить амплитулно-частотные спектры сигналов, указанные в таблице 2.1.

Вариант 8: периодическая последовательность прямоугольного импульса, ЧМ_п , АМ-АМ.

1. Периодическая последовательность прямоугольного импульса.

Порядок выполнения:

1. Исходные данные:

1. Частота повторения прямоугольных импульсов – 80 Гц.

2. Скважность импульсов – 5.

3. Амплитуда прямоугольных импульсов – 8 В.

2. Выражение для сигнала:

т. Е.илии

Следовательно, напряжение можно представить рядом Фурье:

3. Выражение для расчета составляющих спектра:

4. Определим фактическую ширину полосы частот:

Число подлежащих учету гармоник k, если требуется учесть все гармонические составляющие сигнала, амплитуды которых более 0,2 от амплитуды первой, может быть получено из выражения гармоники:

Таким образом, практическая ширина спектра равной 5Ω и составляет 400 Гц, в ней размещаются четыре гармоники и постоянная составляющая.

5. Рассчитаем амплитуды составляющих спектра:

Таблица 1

Составляющие на частотах	Амплитуда, В	Частота, Гц
0	1,6	0
Ω	3	80
2Ω	2,4	160
3Ω	1,6	240
4Ω	0,74	320
5Ω	0	400
6Ω	0,5	480
7Ω	0,7	560
8Ω	0,6	640
9 Ω	0,33	720
10 Ω	0	800

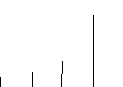
6. Построим амплитудно-частотный спектр сигнала:

Спектр сигнала в соответствии с приведенной выше таблицей имеет вид:

3

2,4

1,6

1,6

0,74 0,7

0,5 0,6 0,33

0 0

0 Ω 2Ω 3Ω 4Ω 5Ω 6Ω 7Ω 8Ω 9Ω 10Ω

7. Определим мощность сигнала на сопротивлении 1 Ом:

Вывод: Спектр периодической последовательности прямоугольного импульса содержит составляющие, приведенных в таблице 1, занимает полосу частот равную 400 Гц, суммарная мощность равна 11,5 Вт.

2. Частотная монипуляция (чМп)

Порядок выполнения:

1. Исходные данные:

1. Частота модулирующего сообщения F_c = 80 Гц.

2. Частота непрерывной или импульсной поднесущей F_п = 1600 Гц.

3. Индексы m_ЧМП=5.

4. Скважность дискретного модулирующего сообщения - 5.

5. Амплитуда поднесущей – 16 В.

2. Выражение для сигнала ЧМ_п:

ЧМП-сигнал можно записать в виде:

где U – амплитуда носителя; ω = 2πf – девиация частоты, т. е. величина максимального отклонения мгновенной частоты от несущей. После тригонометрического преобразования получим:

где – изменение фазы в результате частотной манипуляции.

Частота изменяется через равные промежутки времени от нижней рабочей частоты F_min = F₁-F к верхней F_min = F₁+F и обратно. Легко найти, что переходная фаза будет меняться по пилообразному закону, так как:

или _max= m/ 2 , где m = ω/ – индекс частотной манипуляции.

В выражении cos и sin – периодические функции, так как изменение фазы происходит периодически. Периодические функции f₁ = cosи f ₂ = sin можно разложить в ряды Фурье:

и тем самым найти спектр сигнала.

При вычислении коэффициентов a₀ , a_k и b_k следует учесть, что в интервале времени от 0 до Т/2 (или π) фаза изменяется по закону = m(t – π/2), в интервале времени от Т/2 (или π) до Т (или 2π) – по закону = m(3 π / 2 -t) .

Тогда для функции f₁(t) = cos получим:

при чётном k; при нечётном

,

при всех k.

Аналогично для функции получим:

; ;

при нечётном k и при чётном k.

В результате напряжение после частотной манипуляции записывается в виде:

3. Заменив произведение косинусов и произведение синуса на косинус, окончательно получим выражение для расчета составляющих спектра:

4. Определим фактическую ширину полосы частот, занимаемой сигналом ЧМ_п:

5. Рассчитаем амплитуды составляющих спектра:

Таблица 2

Составляющие на частотах	Амплитуда, В	Частота, Гц
ω	2,03	1600
ω - Ω	0	1520
ω + Ω	0	1680
ω - 2Ω	2,42	1440
ω + 2Ω	2,42	1760
ω - 3Ω	0	1360
ω +3Ω	0	1840
ω - 4Ω	5,64	1280
ω +4Ω	5,64	1920
ω - 5Ω	0	1200
ω +5Ω	0	2000
ω - 6Ω	4,61	1120
ω +6Ω	4,61	2080
ω - 7Ω	0	1040
ω +7Ω	0	2160
ω +8Ω	1,3	2240
ω - 8Ω	1,3	960
ω +9Ω	0	2320
ω - 9Ω	0	880
ω - 10Ω	0,68	800
ω +10Ω	0,68	240
ω - 11Ω	0	720
ω +11Ω	0	2480
ω +12Ω	0,42	2560
ω - 12Ω	0,42	640

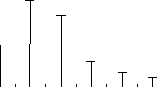
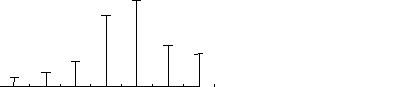
6. Построим спектр сигнала:

Спектр сигнала в соответствии с приведенной выше таблицей имеет вид:

5,65 5,65

4,61 4,61

2,42 2,03 2,42

1,3 1,3

0,42 0,68 0,68 0,42

0 0 0 0 0 0 0 0 0 0 0 0

ω-12Ω ω-10Ω ω-8Ω ω-6Ω ω-4Ω ω-2Ω ω ω+2Ω ω+4Ω ω+6Ω ω+8Ω ω+10Ω ω+12Ω

7. Определим мощность сигнала на сопротивлении 1 Ом:

Мощность ЧМ сигнала на единичном сопротивлении определяется выражением:

Вывод: Спектр ЧМП сигнала состоит из бесконечного числа боковых частот, отличающихся от несущей частоты на , практически ширина полосы частот равна 960 Гц, средняя за период мощность 62,67 Вт.

3. Амплитудно-частотный спектр сигнала АМ-АМ

Порядок выполнения:

1. Исходные данные:

1. Частота модулирующего сообщения F_c = 80 Гц

2. Амплитуда модулирующего сообщения U_c = 8 В

3. Частота непрерывной или импульсной поднесущей F_п = 1600 Гц

4. Частота несущего колебания F_н = 160 000 Гц

5. Амплитуда поднесущей U_п = 16 В

6. Коэффициенты глубины амплитудной модуляции m_АМ = 0,8; M = 1.

2. Выражение для сигнала АМ-АМ:

Согласно условию задачи модулирующее сообщение описывается выражением:

поднесущая:

несущая:

согласно определению сигнал АМ может быть представлен в виде:

Подставив и в получим:

где

Тогда АМ-АМ сигнал принимает вид:

,

где - коэффициент амплитудной модуляции на второй ступени.

Отсюда найдем ,приняв коэффициент .

3. Выражение для расчета составляющих спектра:

Преобразуем U_АМ-АМ(t) и окончательно получим:

4. Опр. фактическую ширину полосы частот, занимаемой сигналом АМ:

5. Рассчитаем амплитуды составляющих спектра:

Таблица 4

Сост-щие на частотах	Амплитуда, В	Частота, Гц
Fн	16	160 000
Fн - Fп	8	158 400
Fн + Fп	8	161 600
Fн + Fп + Fc	3,2	161680
Fн + Fп - Fc	3,2	161520
Fн - Fп + Fc	3,2	158480
Fн - Fп - Fc	3,2	158320

6. Построим амплитудно-частотный спектр сигнала:

Спектр сигнала в соответствии с приведенной выше таблицей имеет вид:

16

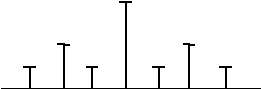
8 8

3,2 3,2 3,2 3,2

15,832 15,84 15,848 16 16,152 16,16 16,168

7. Определим мощность сигнала на сопротивлении 1 Ом:

Мощность АМ-АМ сигнала на единичном сопротивлении определяется выражением:

.

Вывод: Спектр АМ-АМ сигнала содержит семь составляющих на частотах, приведенных в таблице 4, занимает полосу частот равную 3,36 кГц, суммарная мощность всех составляющих равна 212,48 Вт.