I Исследование линейной непрерывной сау

Исходные данные

Структура исследуемой замкнутой линейной непрерывной САУ представлена на рис.1.1, где – управляющее воздействие, – возмущающее воздействие,- сигнал ошибки,- выходной сигнал. Значения параметров , , заданы в табл. 1. Размерность , , в секундах, общий коэффициент передачиимеет размерность 1/с, в табл. 1 заданы также желаемые показатели качества системы: максимальная ошибка по скоростипри скачке по скоростии, время переходного процессав секундах, и перерегулированиев процентах.

Исходные данные приведены в табл.1

Таблица 1

Номер варианта	1	eck	tnn	σ
15	2,8	0,06	3,8	10	0,23	1	4,8

Рис.1.1

1. Требуемые передаточные функции находят с использованием правил структурных преобразований. Коротко сформулируем основные правила.

• Передаточные функции последовательно соединенных звеньев перемножаются.

• Передаточные функции параллельно соединенных звеньев складываются.

• Передаточная функция системы с обратной связью – это передаточная функция замкнутой системы, которая определяется по формуле:

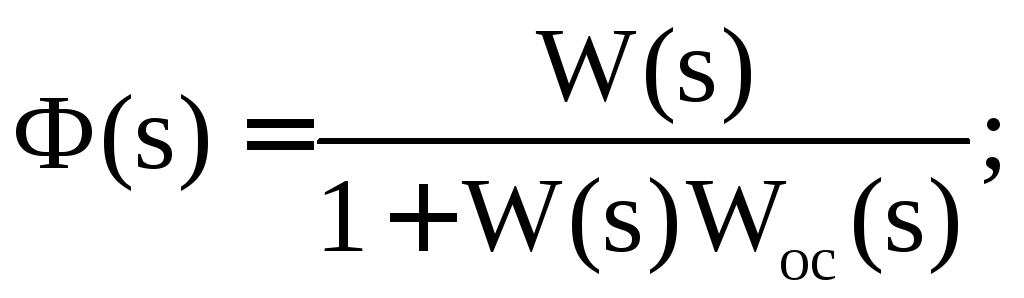
Например, для системы, представленной на рис. 1.2 можно записать следующие передаточные функции:

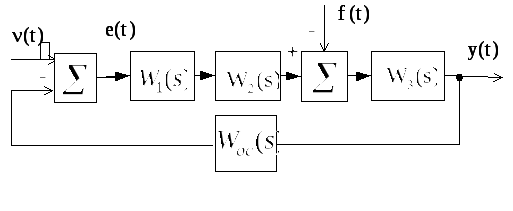
Рис.1.2

Передаточная функция разомкнутой системы при,(т.е. разомкнута главная обратная связь) определится выражением

где обозначено ,

,

.

Главная передаточная функция или передаточная функция замкнутой системы при :

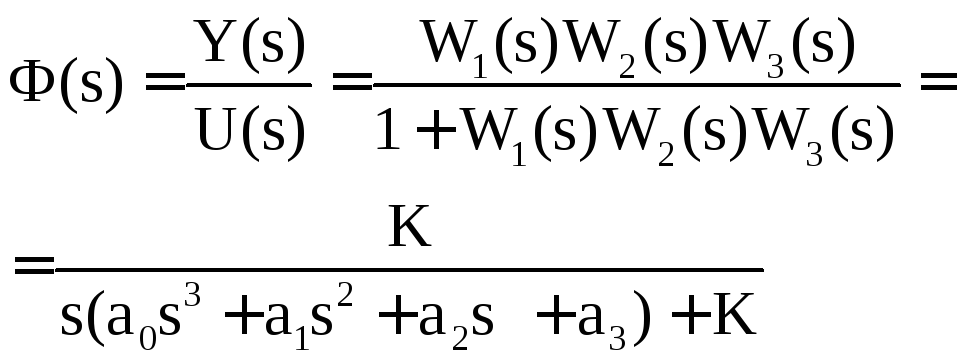
Передаточная функция по ошибке при , которая позволяет выразить ошибку e(t) в системе при известном входном воздействии:

Передаточная функция по возмущению при позволяет выразить влияние возмущения на выходной сигнал:

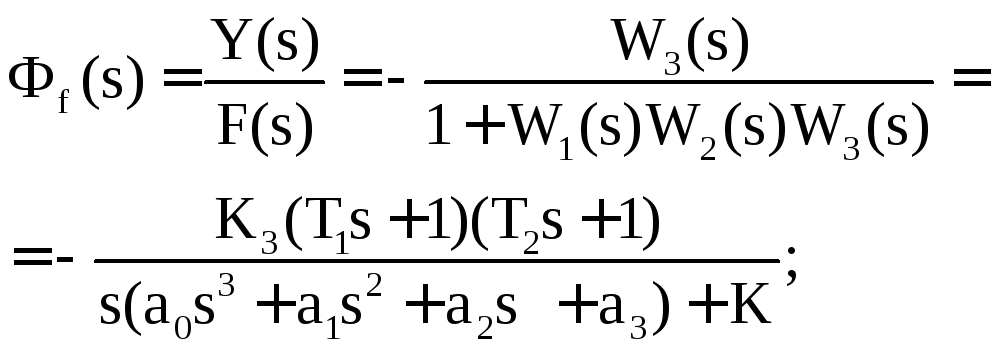
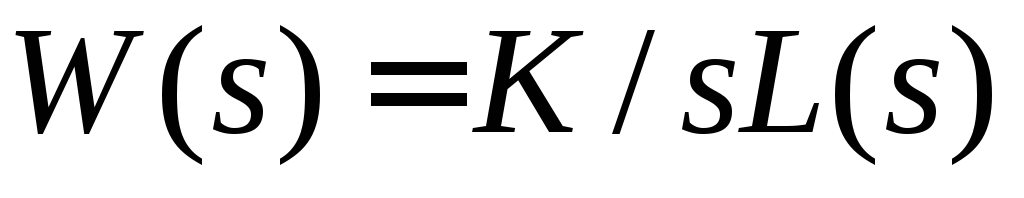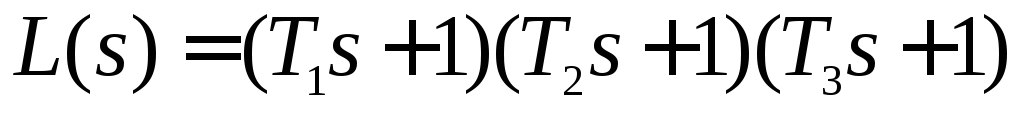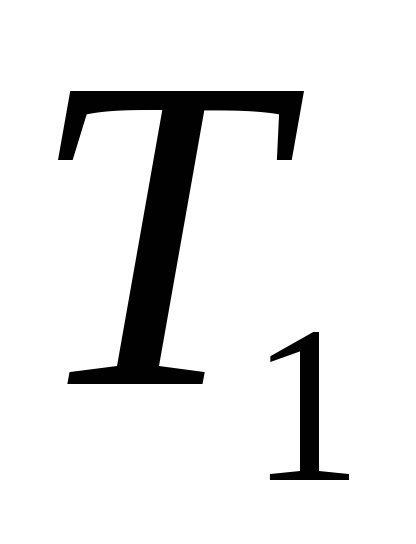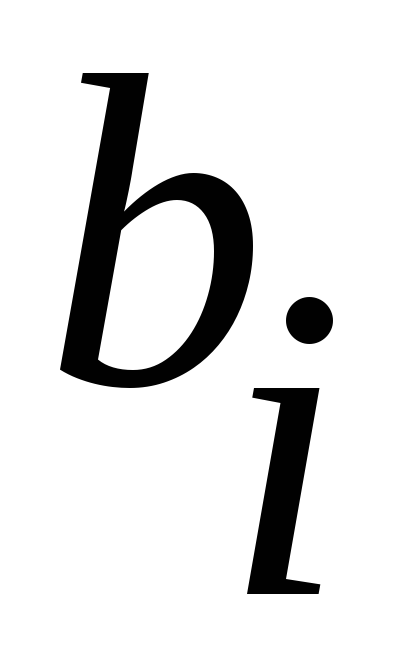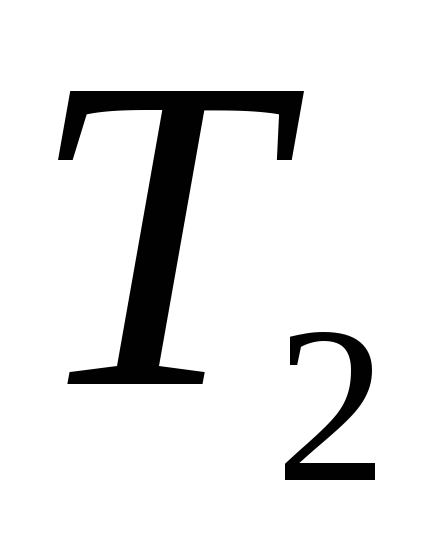2. Передаточная функция разомкнутой исходной системы имеет вид , где. Характеристическое уравнение замкнутой системы будет, где при заданных из таблицы исходных данных числовых значениях и коэффициентыбудут зависеть от параметрови . Применение критерия Гурвица к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:.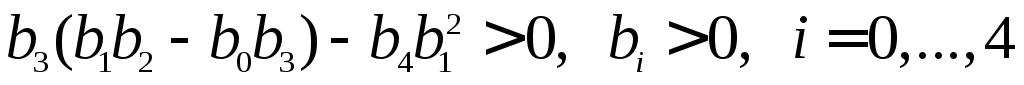

Приравнивая в написанных соотношениях правые части нулю, найдем зависимость от и построим в плоскостии границы устойчивости, ограничивающие некоторую область устойчивости. При заданном параметре находим граничное значение коэффициента передачи.

где обозначено

,

,

,

Выразим К через параметр Т₂.

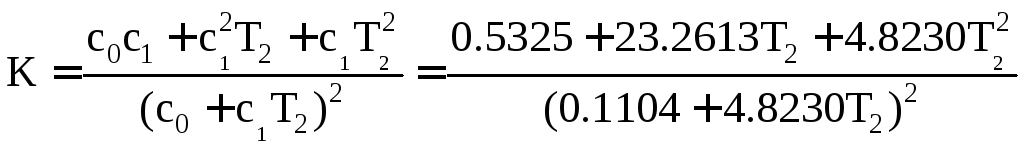
Зависимость К(Т₂) приведена на рис.1.3.

Рис.1.3

При заданном параметре находим граничное значение коэффициента передачи.

K_гр=K(T2=0.1)= 8.2746.

3. Полагая , записываем аналитическое выражение для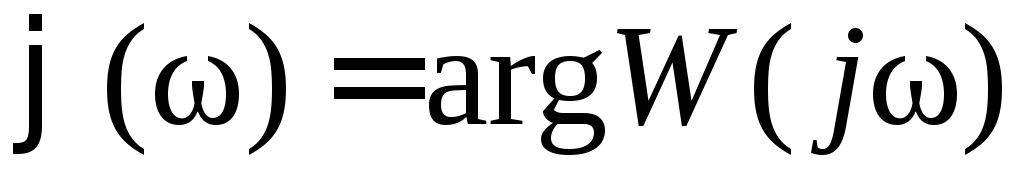,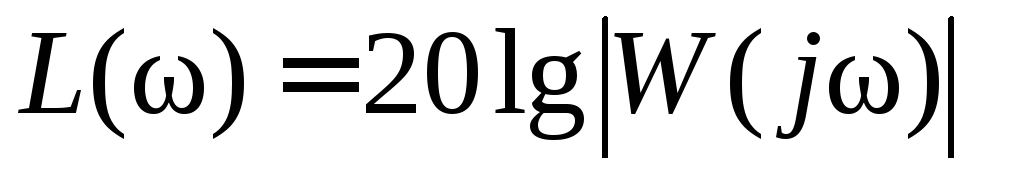изпри.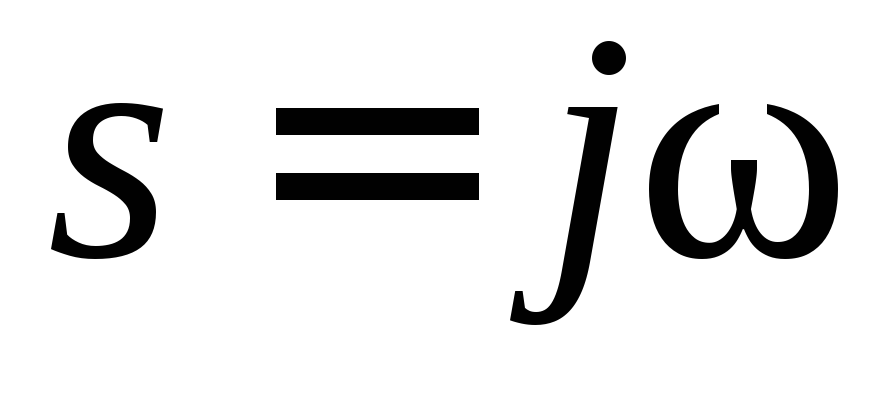

К=0.7K_гр= 5.7922.

Передаточную функцию разомкнутой системы можно записать в виде

где

Тогда

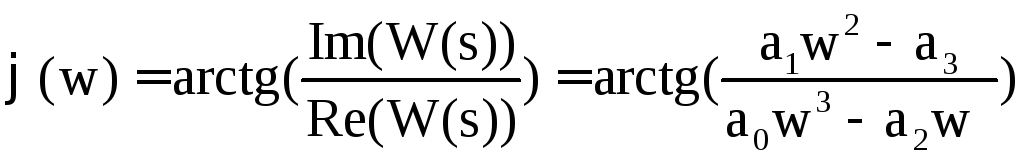
где

Строим графики логарифмических характеристик разомкнутой системы, с помощью MATLAB(оператор bodeилиmargin) Рис.1.4 а. Предварительно с помощью функцииpaz=tf([K],[a0 a1 a2 a3 0]) найдем

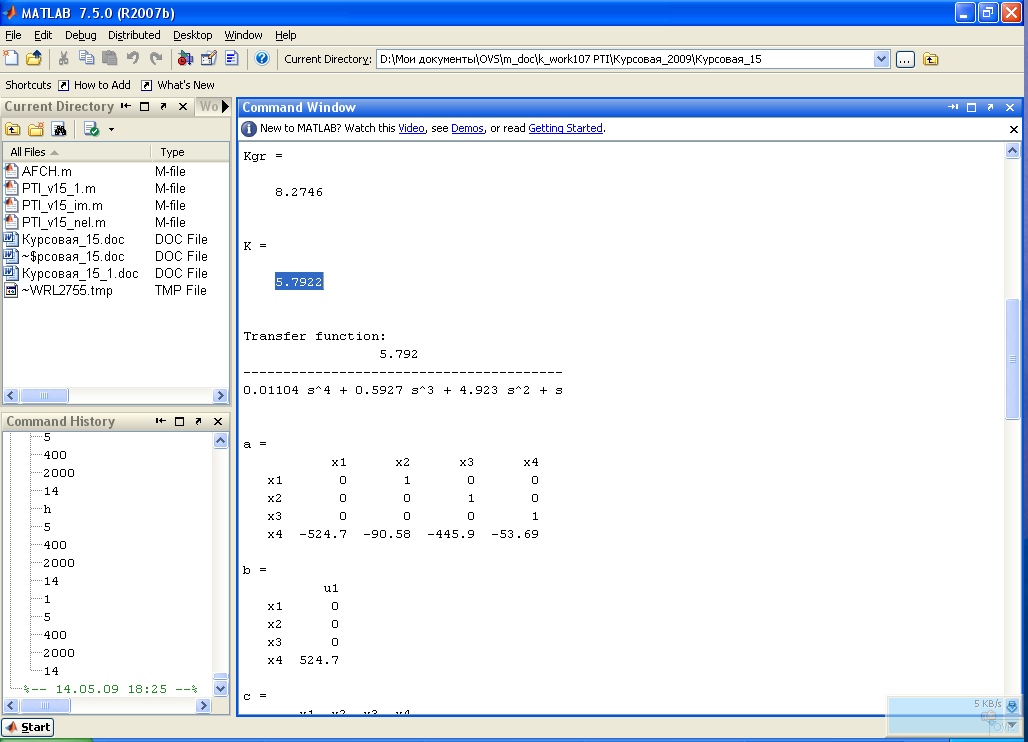
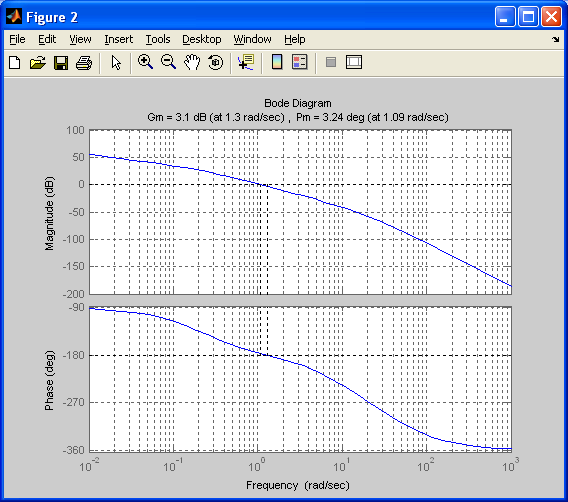
Рис.1.4 а

Вещественная часть частотной характеристики замкнутой системы

Строим график АФЧХ с помощью MATLAB(оператор nyquist) рис.1.4 б для разомкнутой системы.

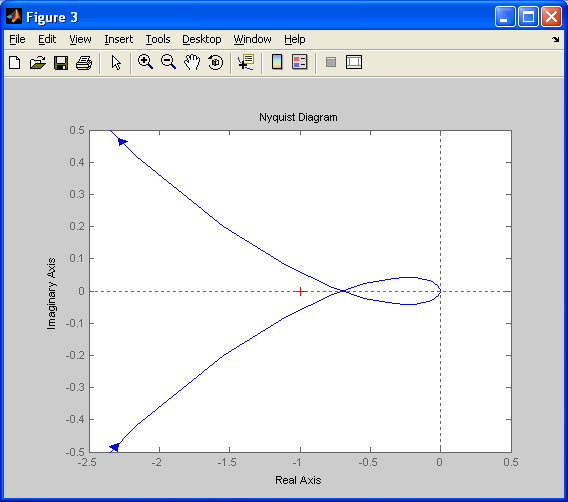
Рис.1.4 б

Запасы устойчивости по модулю и фазе определяются по логарифмическим характеристикам (см. рис.1.4 а): на частоте среза ω_сопределяетсязапас по фазе – , азапас по амплитуде – на частоте при которой. Таким образом,, что является недостаточным.

4. Величина ошибки по скорости определяется как 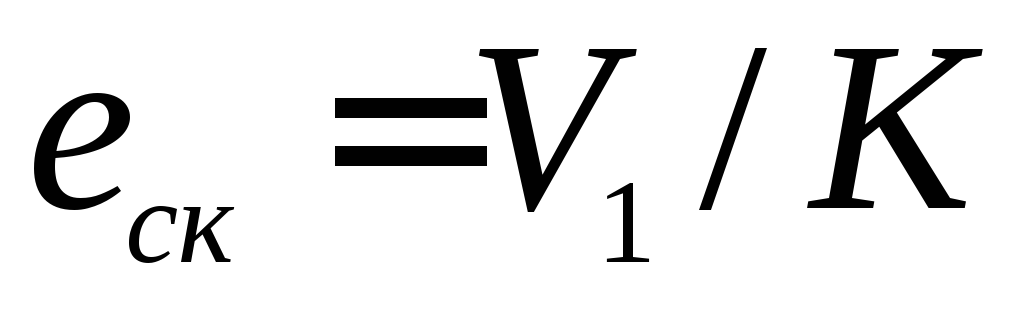. Для ориентировочной оценкиt_nnи σ следует построить переходной процесс(операторstepвMATLAB) при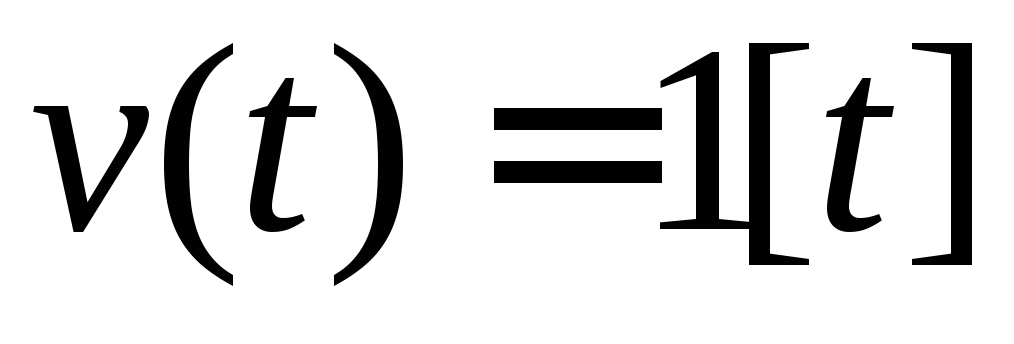и по нему определитьt_nnи σ.

Для получения уравнений состояний в нормальной форме используем дифференциальное уравнение замкнутой системы . Если, то уравнение состояния имеет вид

Для описания динамических систем в пространстве состояний в Matlab 7.* применяются модели подкласса ss, которые основаны на линейных дифференциальных или разностных уравнениях.

Модель непрерывной системы в подклассе ss имеет вид:

dx/dt = Ax + B;

y = Cx + D,

где: х - вектор состояния; u- вектор входа; у - вектор выхода.

Для формирования моделей в подклассе ss предназначена функция ss

sys = ss(A, В, С, D).

В результате под именем sys получаем ss-объект с числовыми характеристиками в виде четверки матриц {А, В, С, D}, которые должны иметь согласованные размеры. МатрицуDв данном случае полагаем равной 0.

Для построения переходного процесса воспользуемся операторомstepвMATLAB.

Реализация функций имеет вид:

sys=ss([0 1 0 0;0 0 1 0;0 0 01;-b4/b0 -b2/b0 -b1/b0],[0 0 0 K/b0]',eye(4),zeros(4,1));

step(sys)

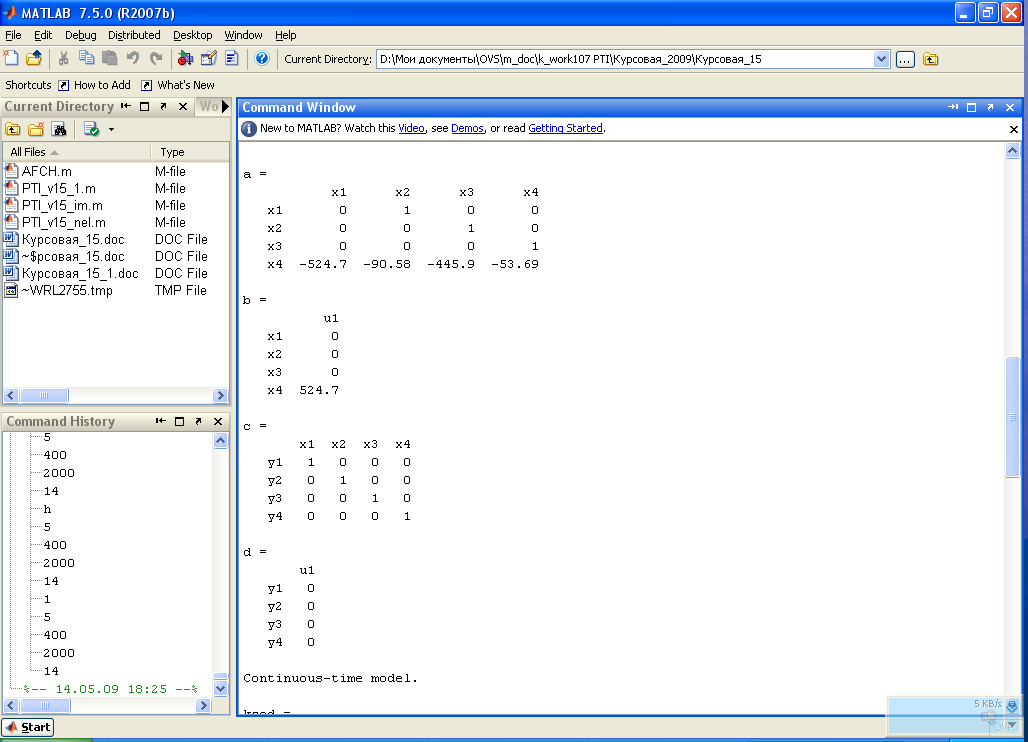
В результате получим графики представленные на рис.1.5. Нас будет интересовать Out(1).

Величина ошибки по скорости определяется как .

Для ориентировочной оценки t_nnи σ следует построить переходной процесс(операторstepвMATLAB) прии по нему определитьt_nnи σ. Эти величины из графикаOut(1) определяются следующим образом:

,

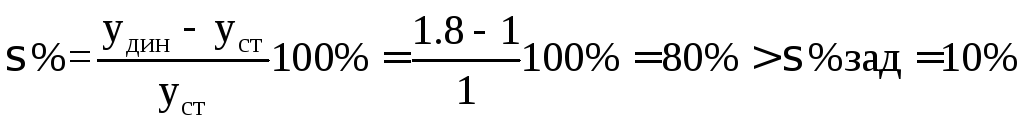Время переходного процесса определяется с учетом следующих соотношений: ε_уст=(t)/(1+K), где, а К=5.7922 – общий коэффициент передачи разомкнутой системы. Тогда ε_уст=1/(1+1.964)= 0.15 и следовательноt_nnиз графикаOut(1).

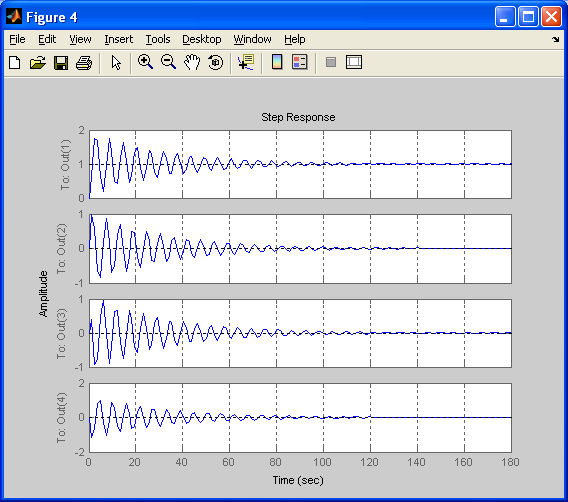
Рис.1.5

Таким образом. исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать.

5. Если исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. В случае применения частотных методов синтеза коррекции строится желаемая ЛАЧХ . В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма (наличие интегратора 1/sв системе) требуемый коэффициент усиления выбирается из соотношения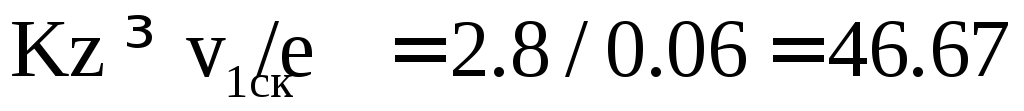. На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном -40(если необходимо -60) дБ/дек, а высокочастотная часть желаемой исходной ЛАЧХ по возможности должны совпадать.

Учет требований качества переходного процесса: t_nnи σ, запасов устойчивости учитываются при формировании среднечастотной области. Здесь можно воспользоваться графиком (рис.1.6).

Рис.1.6

По графику рис.1.6 для заданных значений инаходяти затем из соотношениячастоту среза.

В наше случае: (как показано на рис.1.6,а) для ,,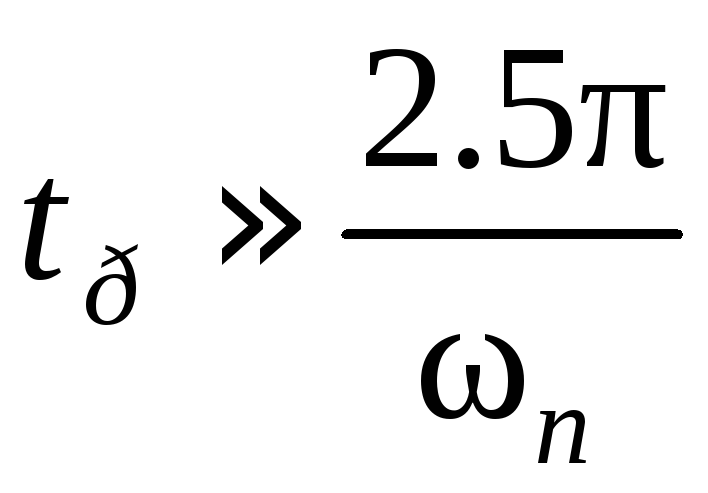 откуда для, значениеи.

Сопряжение среднечастотного участка с низкочастотным и высокочастотным (рис. 1.7) должно быть таким, чтобы была проще коррекция и чтобы изломы, по возможности, были не более чем на (протяженность участка около декады). Тогда, выберемна частотеина частоте.

Введем обозначения:

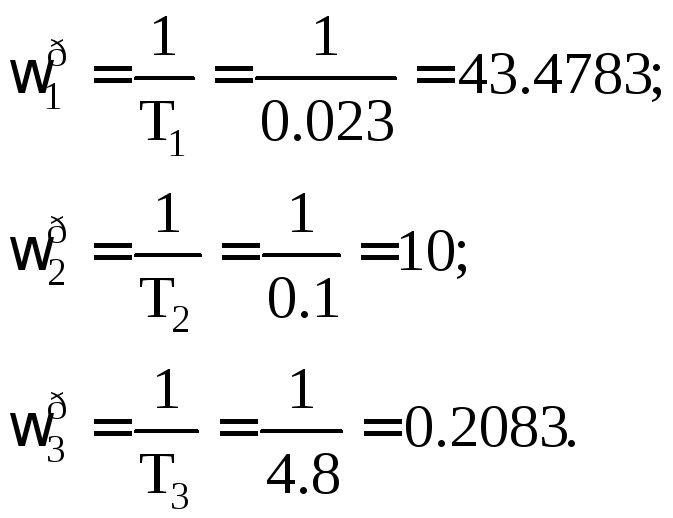
Величину ω₁ найдем из условия равенства значений. Это соотношение приводит к следующему выражению:

В последнем выражении обозначено:

ω'=0.1ω₂

L’(ω')=50 дБ

L’(ω₂)=10 дБ

L(ω₃^р)=L(0.2083)= 25.8695 дБ

L(ω₂)=L(0.25)= 23.4214 дБ

Последние две величины находятся из выражения для L_исх(ω).

Найденное по формуле значение ω₁=0.1372

ЛАЧХ с корректирующего устройства с характеристикой L_k(ω), приведенной на рис.1.7, соответствует функция (рис.1.7):

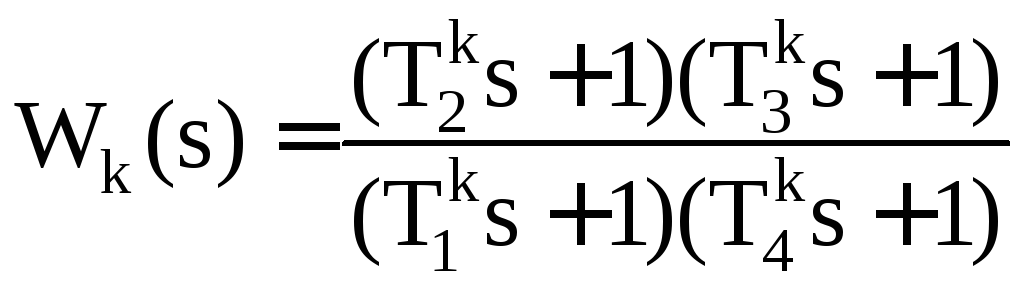
где

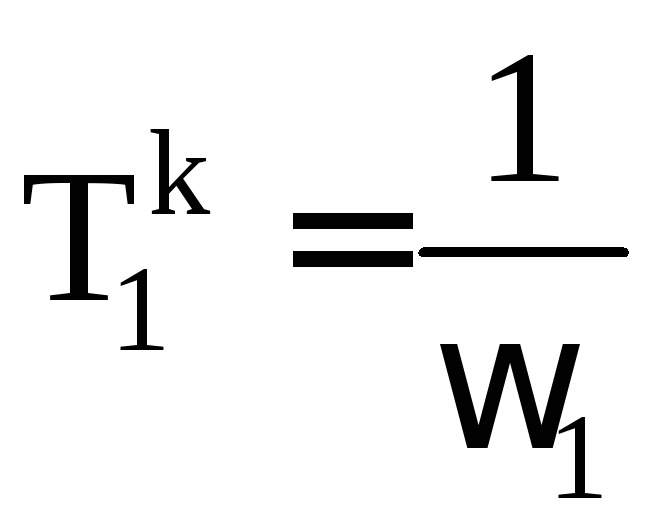
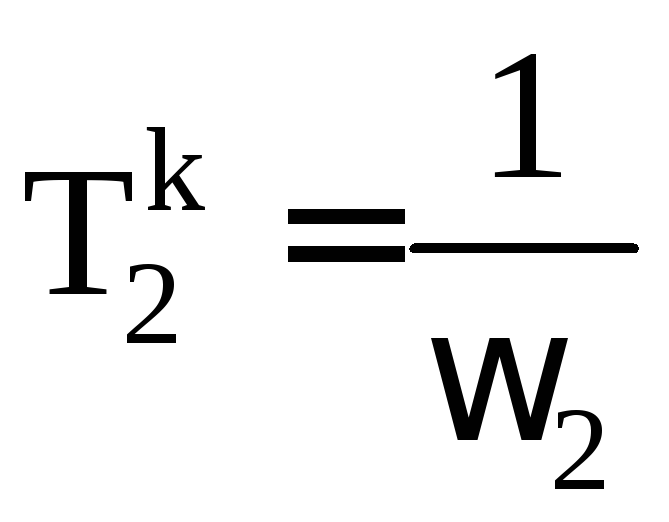
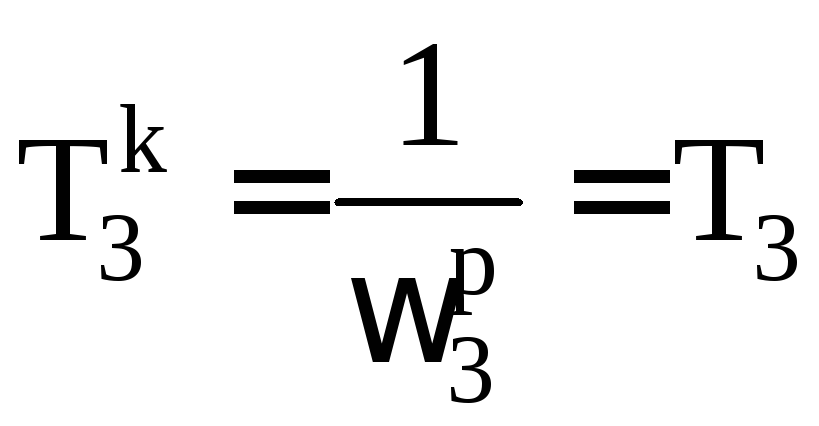
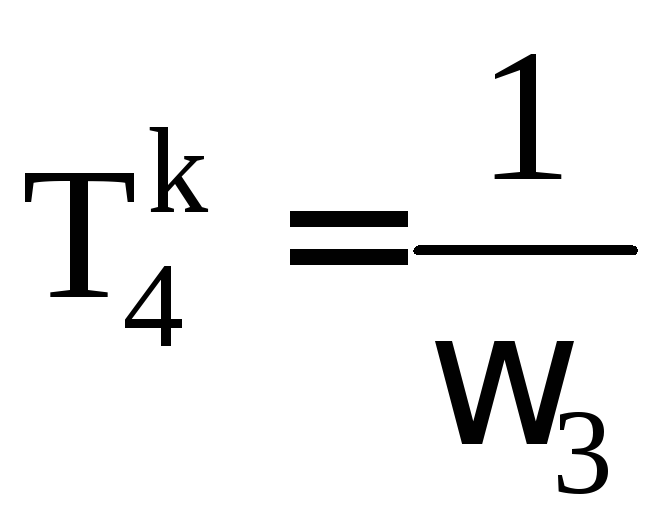
Рис. 1.7.

Общая передаточная функция разомкнутой системы с корректирующим звеном последовательного типа имеет вид

где .

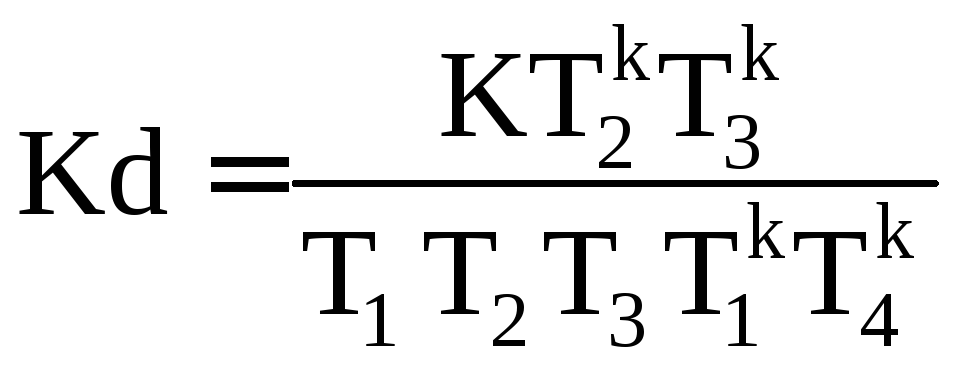Далее воспользуемся функцией zpk(z, р, К), где z и р – векторы из нулей и полюсов, а Кd – обобщенный коэффициент передачи, sys – любое имя присваиваемое модели. Тогда запись в системе Matlab примет вид

sys1=zpk([-1/T2k -1/T3k],[0 -1/T1 -1/T2 -1/T3 -1/T1k -1/T4k],Kd)

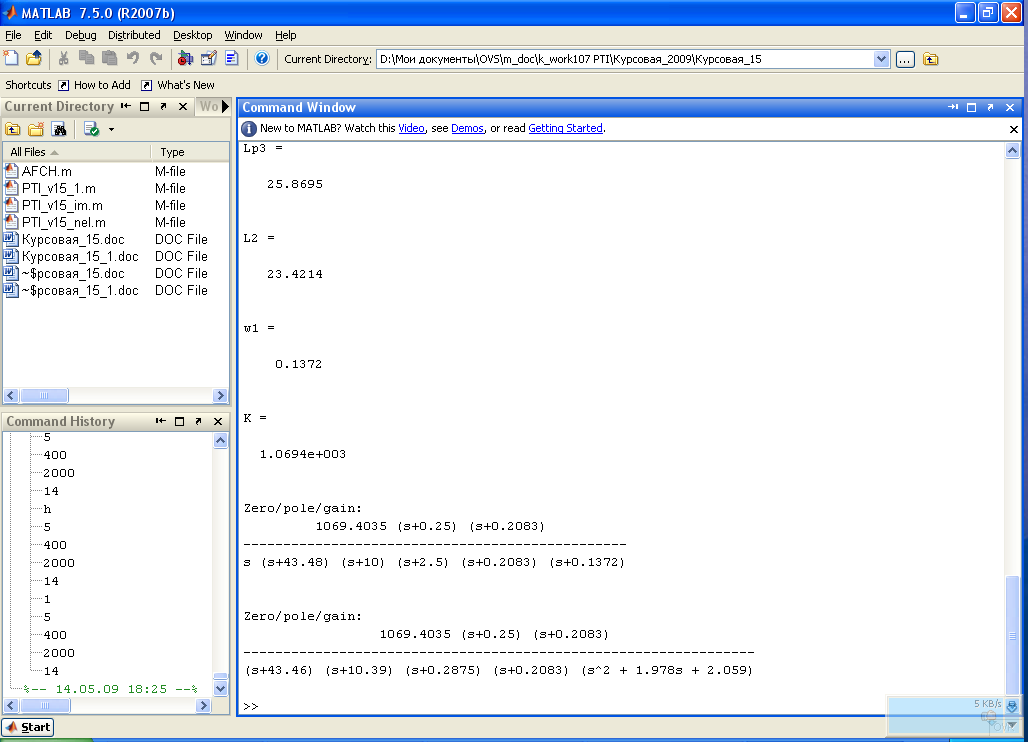
Результат представления sys1 представлен ниже.

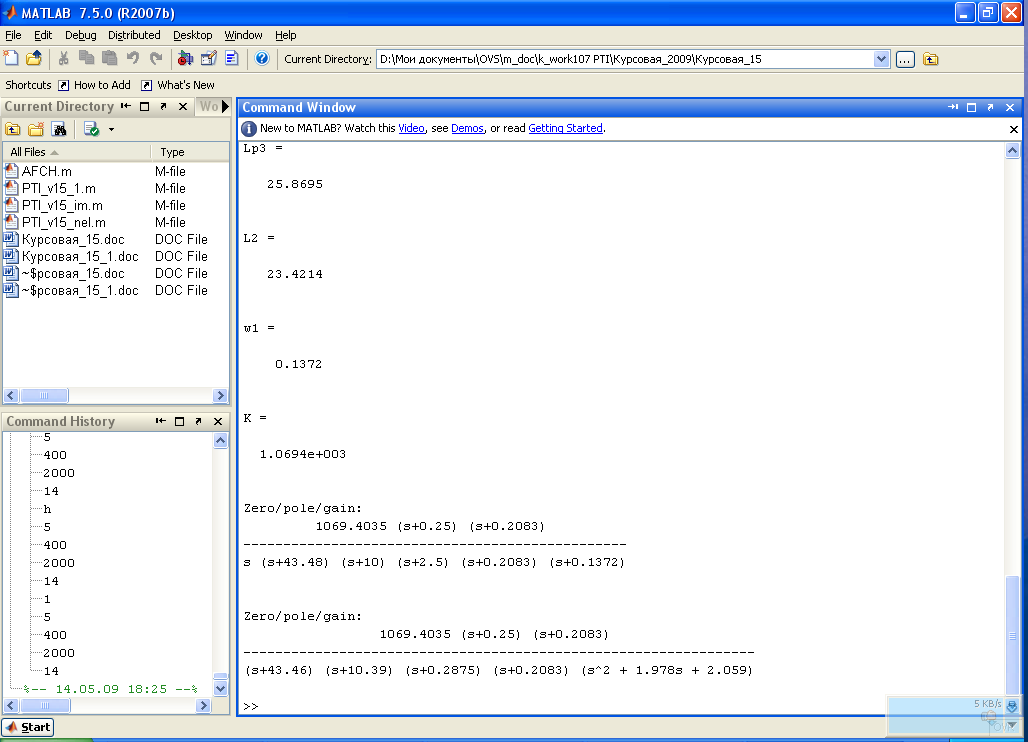
Диаграммы Боде (margin(sys1)) представлены на рис.1.8. На диаграмме также обозначены запасы устойчивости, которые являются приемлемыми.

Рис.1.8

Для нахождения переходных характеристик замкнутой системы с корректирующим звеном предварительно сформируем модель в пространстве состояний.

Передаточная функция замкнутой системы имеет вид

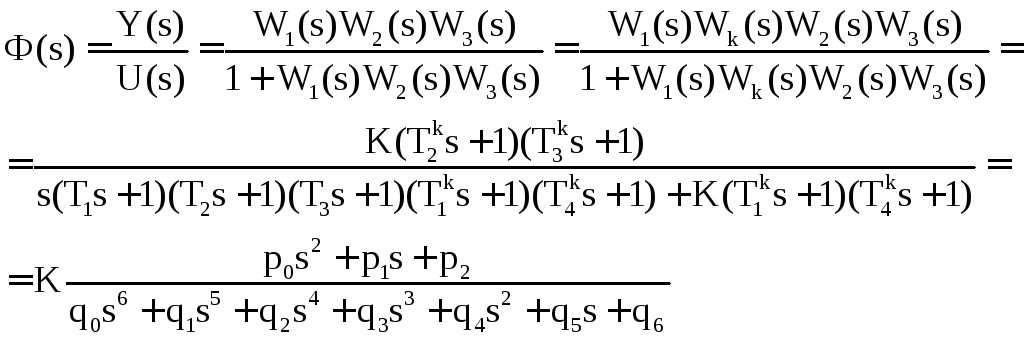
Для нахождения Ф(s) воспользуемся следующей последовательностью команд

sys1=zpk([-1/T2k -1/T3k],[0 -1/T1 -1/T2 -1/T3 -1/T1k -1/T4k],K)

Zam_ck=feedback(sys1) – находится передаточная функция замкнутой системы.

Переходная характеристика (рис.1.9 ) находится с помощью функций:

sys3=ss(Zam_ck)

Из рассмотрения рис. 1.9 видно, что параметры по заданию выполняются.

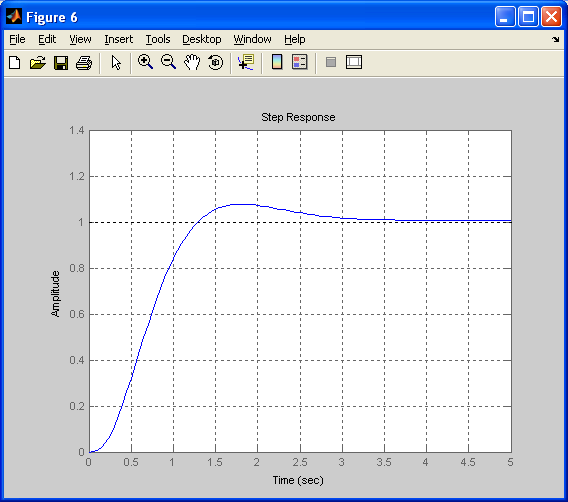
Рис.1.9