КР Телемеханика
.docx
Задание 1.1. Рассчитать и построить
амплитудно-частотный спектр ФМП сигнала
и определить полосу частот, если частота
модулирующего сообщения
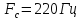 , частота несущей
, частота несущей
 ,
амплитуда несущей
,
амплитуда несущей
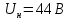 .
.
Решение: Выражение для ФМП сигнала:
|
|
(1.1) |
где
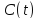 – модулирующий сигнал в виде
последовательности прямоугольных
– модулирующий сигнал в виде
последовательности прямоугольных
импульсов,
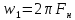 ,
,
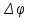 —величина
изменения начальной фазы
—величина
изменения начальной фазы
Согласно [1] выражение для расчета составляющих спектра ФМП сигнала:
|
|
(1.2) |
Выражения
для расчета спектра ФМП сигналы при
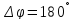 :
:
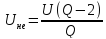
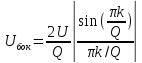
Практическая ширина спектра ФМП сигнала:
|
|
(1.3) |
Подставим числовые значение в (1.2):
|
|
(1.4) |
Расчет амплитуд и частотных составляющих ФМП сигнала сведем в таблицу 1.1.
Таблица 1.1 – Значения амплитуд и частот гармонических составляющих ФМП сигнала
|
Составляющие на частотах |
Амплитуда, В |
Частота, Гц |
|
|
26 |
4400 |
|
|
16 |
4620 |
|
|
16 |
4180 |
|
|
13 |
4840 |
|
|
13 |
3960 |
|
|
8.9 |
5060 |
|
|
8.9 |
3740 |
|
|
4.1 |
5280 |
|
|
4.1 |
3520 |
|
|
0 |
5500 |
|
|
0 |
3300 |
Спектр ФМП сигнала в соответствии с таблицей 1.1 имеет вид:

Рисунок 1.1– Амплитудно-частотный спектр ФМП сигнала
Мощность ФМП сигнала на единичном сопротивлении:
|
|
(1.5) |
Вывод. Спектр ФМП сигнала занимает полосу частот равную 2200 Гц, на которой содержится 11 составляющих на частотах, приведенных в таблице, суммарная мощность всех составляющих равна 1900Вт.
Задание 1.2. Рассчитать и построить
амплитудно-частотный спектр АМ сигнала
и определить полосу частот, если частота
модулирующего сообщения
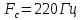 , частота несущей
, частота несущей
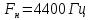 ,
амплитуда несущей
,
амплитуда несущей
 ,
коэффициент глубины амплитудной
модуляции
,
коэффициент глубины амплитудной
модуляции
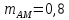 .
.
Решение:
Согласно исходным данным модулирующее сообщение описывается выражением для АМ сигнала:
|
|
(1.6) |
Несущая
|
|
(1.7) |
Выражение для АМ-сигнала:
|
|
(1.8) |
где
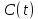 – модулирующий сигнал в виде
последовательности прямоугольных
импульсов, k—коэффициент
пропорциональности,
– модулирующий сигнал в виде
последовательности прямоугольных
импульсов, k—коэффициент
пропорциональности,
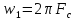 .
.
Согласно [1] выражение для расчета составляющих спектра АМ- сигнала:
|
|
(1.9) |
Полоса частот, занимаемая АМ-сигналом:
|
|
(1.10) |
Подставим численные значение в (1.9):
|
|
Расчет амплитуд и частотных составляющих АМ сигнала сведем в таблицу 1.2.
Таблица 1.2 – Значения амплитуд и частот гармонических составляющих АМ сигнала
|
Составляющие на частотах |
Амплитуда, В |
Частота, Гц |
|
|
44 |
4400 |
|
|
17.6 |
4180 |
|
|
17.6 |
4620 |
Спектр АМ сигнала в соответствии с таблицей 1.2 имеет вид:
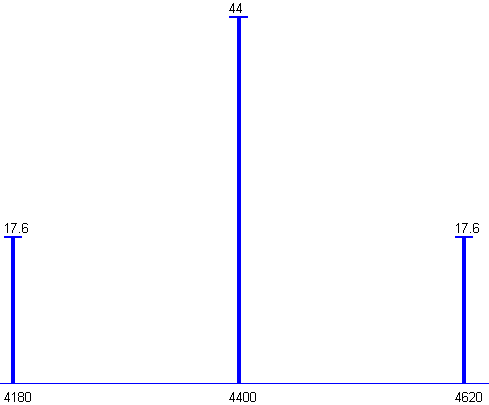
Рисунок 1.2 – Амплитудно-частотный спектр АМ сигнала
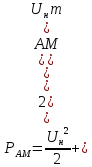
Мощность АМ сигнала на единичном сопротивлении:
|
|
(1.11) |
Вывод. Спектр АМ сигнала содержит три составляющих на частотах, приведенных в таблице, занимает полосу частот равную 440 Гц, суммарная мощность всех составляющих равна 1000Вт.
Задание 1.3. Рассчитать и построить амплитудно-частотный спектр АМ-АМ сигнала и определить полосу частот, если амплитуда модулирующего сигнала
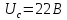 ,
амплитуда поднесущей
,
амплитуда поднесущей
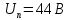 ,
частота несущей
,
частота несущей
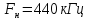 ,
частота поднесущей
,
частота поднесущей
 ,
частота модулирующего сигнала
,
частота модулирующего сигнала
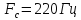 , коэффициент глубины модуляции на
первой ступени
, коэффициент глубины модуляции на
первой ступени
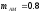 ,
на второй
,
на второй
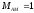 .
.
Решение: Модулирующее сообщение описывается выражением
|
|
(1.12) |
Поднесущая
|
|
(1.13) |
Несущая
|
|
(1.14) |
Амплитудно-модулированный сигнал может быть представлен в виде:
|
|
(1.15) |
Подставив из (1.12) и (1.13) Uc(t) и w1 в (1.15) получим:
|
|
(1.16) |
Тогда АМ-АМ сигнал принимает вид:
|
|
(1.17) |
Амплитуда несущей:
|
|
(1.18) |
где k=1 коэффициент пропорциональности.
Полоса частот, занимаемая АМ-АМ:
|
|
(1.19) |
Подставим числовые значения в (1.15):
|
|
(1.20) |
Расчет амплитуд и частотных составляющих АМ-АМ сигнала сведем в таблицу 1.3.
Таблица 1.3 – Значения амплитуд и частот гармонических составляющих АМ-АМ сигнала
|
Составляющие на частотах |
Амплитуда, В |
Частота, Гц |
|
|
44 |
440000 |
|
|
22 |
444400 |
|
|
22 |
435600 |
|
|
8.8 |
444620 |
|
|
8.8 |
444180 |
|
|
8.8 |
435820 |
|
|
8.8 |
435380 |
Спектр АМ-АМ сигнала в соответствии с таблицей 1.3 имеет вид:
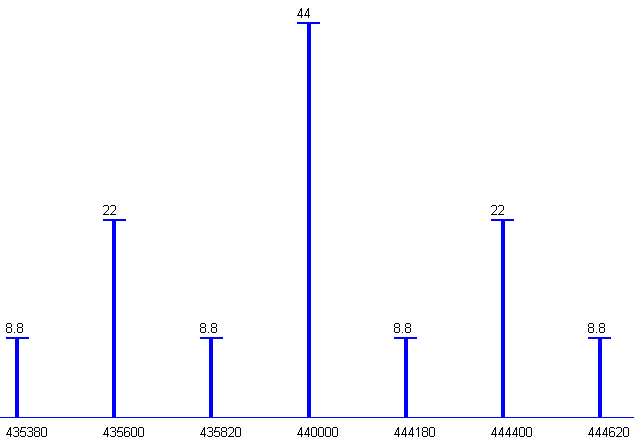
Рисунок 1.3 – Амплитудно-частотный спектр АМ-АМ сигнала
Мощность АМ-АМ сигнала на единичном сопротивлении:
|
|
(1.21) |
Вывод. Спектр АМ-АМ сигнала содержит 7 составляющих на частотах, приведенных в таблице, занимает полосу частот равную 9240 Гц, суммарная мощность всех составляющих равна 1600Вт.
Задание 2.1. Закодировать число 322 в инверсном коде и сделать вывод о корректирующих свойствах.
Решение. Определим число информационных символов из выражения
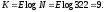 (2.1)
(2.1)
Тогда число 322 в двоичном коде может быть представлено кодовой комбинацией 101000010. Контрольные символы представляют собой прямую запись К–разрядной кодовой комбинации, если число единиц в ней четное, если же нечетное, то инверсную. Число единиц нечетное, следовательно, контрольные символы имеют вид: 010111101. Исходная кодовая комбинация в инверсном коде имеет вид F(x) = 101000010 010111101, т.е. число контрольных символов r = k = 8, а общая длинна n = r + k =9+8=18. Избыточность R = r/n=18/9 = 0,5.
При декодировании анализируется первая половина кодовой комбинации F'(x), пришедшей из канала связи, и, если число единиц в ней четное, то вторая половина принимается в прямом виде, а, если нечетное, то в инверсном виде. Затем обе кодовые комбинации складываются по модулю два и, если синдром (результат проверки) будет нулевого порядка, то искажений нет, в противном случае принятая комбинация F'(x) бракуется. Пусть из канала связи поступила кодовая комбинация F'(x) = 101001010 010111101. Тогда 101001010+010111101 =111110111, т.е. результат указывает, что в принятой кодовой комбинации имеются искажения.
Вывод. Избыточность данного кода не зависит от числа информационных символов и равна 0,5. Необнаружение ошибок имеет место в том случае, когда искажены два символа в исходной кодовой комбинации и соответствующие им два символа в контрольной комбинации.
Задание 2. 2. Закодировать число 322 (101000010) в коде Бергера и сделать вывод о корректирующих свойствах.
Решение. Контрольные символы в этом коде представляют разряды двоичного числа в прямом или инверсном виде количества единиц или нулей, содержащихся в исходной кодовой комбинации.
Определим число контрольных символов:
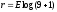 =4,
(2.2)
=4,
(2.2)
Для комбинации F(x)= 101000010 запишем количество единиц в двоичном коде в прямом виде: 0011 – контрольные символы, тогда закодированная комбинация будет иметь вид F'(x)= 101000010 0011.
Пусть кодовая комбинация F(x)
была искажена помехами и поступила в
виде F'(x)= 101010010
0011, где искаженные символы подчеркнуты,
тогда 0100 0011=0111искажение
обнаружено.
0011=0111искажение
обнаружено.
Вывод. Данный код обнаруживает все одиночные и большую часть многократных ошибок.
Задание 2.3. Закодировать число 322 (101000010) кодом Файра с bs = 4 и bm = 5 сделать вывод о корректирующих свойствах.
Решение. Образующий многочлен
кода Файра
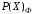 определяется из выражения 2.3
определяется из выражения 2.3
|
|
(2.3) |
где
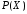 - неприводимый многочлен степени
- неприводимый многочлен степени
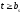
 4,
принимаем t=4
4,
принимаем t=4
Из соответствующих таблиц выбираем
неприводимый многочлен P(X)=
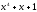 =
10011.
=
10011.
|
|
(2.4) |
принимаем С=8
Находим
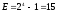 .
Видим, что C на E
нацело не делится. Число контрольных
символов
.
Видим, что C на E
нацело не делится. Число контрольных
символов
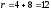 .
Длинна кода равна
.
Длинна кода равна
|
n=НОК |
(2.5) |
В итоге получаем циклический код (120,
108). Образующий многочлен Файра
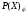 равен
равен
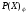 =(
=(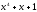 )(
)(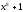 )=
)=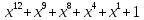 =
=
1001100010011
=
=
1001100010011
Далее кодирование осуществляется так же как при циклическом коде с d=3.
Так как необходимо закодировать только
одно сообщение
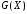 ,
а не весь ансамбль двоичных кодов с
,
а не весь ансамбль двоичных кодов с
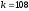 ,
то в дальнейшем будем придерживаться
процедуры кодирования, выполняемой по
уравнению 2.6
,
то в дальнейшем будем придерживаться
процедуры кодирования, выполняемой по
уравнению 2.6
|
|
(2.6) |
Выбираем одночлен
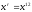 .
Тогда
.
Тогда
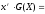 101000010
000000000000
101000010
000000000000
Разделим
полученное выражение на
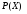

находим
остаток
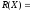 100100111101
100100111101
Следовательно, передаваемая закодированная комбинация будет иметь вид
F(X) = 101000010 100100111101
Пусть кодовая комбинация F(x) была искажена помехами и поступила в виде F'(x)= 101111100 100100111101, где искаженные символы подчеркнуты. Разделим F'(x) на образующий полином:

получили остаток
 110111101110,
следовательно, в полученной комбинации
есть ошибка.
110111101110,
следовательно, в полученной комбинации
есть ошибка.
Вывод. Код Файра с ds = 4 и dm = 5 может обнаруживать пакеты ошибок длиной равной 5.

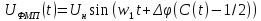
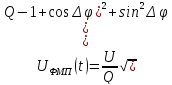
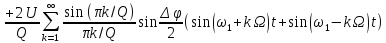
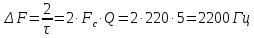
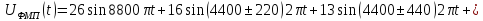
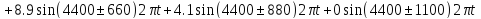
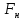
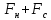
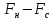
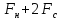
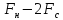
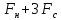
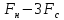
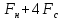
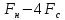
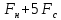
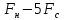
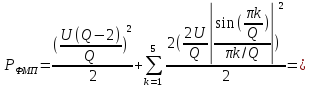
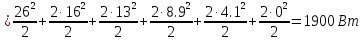
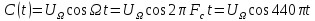
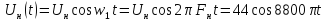
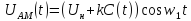
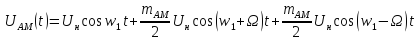
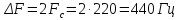
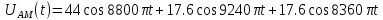


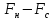


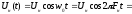
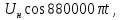
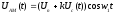


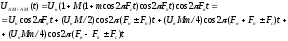
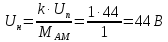
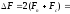
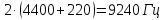
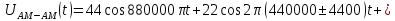
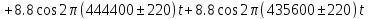

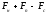


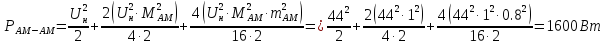
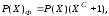
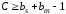
 4+5-1
4+5-1 8,
8,
 =НОК(15,8)
= 120
=НОК(15,8)
= 120