3. Пример прогнозирования продаж

Имеются данные по квартальным продажам 2006-2009 гг.

Таблица 5 - Среднедневная реализация, т

Квартал	2006	2007	2008	2009
I	49,9	48,1	50,9	60,7
II	75,8	92,3	106,5	120,6
III	73,9	93,4	108,8	126,7
IV	48,5	55,1	68,8	70,5
Годовая	62,0	72,2	83,8	94,6
Темпы роста, в % к 2006 г.	100	116,4	135,0	152,6
в % по годам	-	116,4	116,0	113,0
Абсолютный прирост по годам, m	-	10,2	11,5	10,9
Темп наращивания, %	-	16,4	18,6	17,5

Из таблицы 5 видно, что в 2009 г. рост продаж по сравнению с 2006 г. достиг 152,6%, или в среднем за год интенсивность роста составила 115,1% . Это позволяет считать, что в анализируемом году динамики имеется значительная тенденция роста.

Графическое изображение исходной информации подтверждает эти выводы (рис. 1).

Рисунок 1 – Реализация по кварталам 2006-2009 гг.

Выводы о значительном росте реализации в 2006 – 2009 гг. предопределяет расчет индексов сезонности способом переменной средней.

По содержащимся в таблице 5 показателям анализируемого ряда динамики можно выдвинуть рабочую гипотезу о возможных типах математических функций для получения теоретических уровней тренда.

С известной степенью приближения это может быть прямолинейная функция:

.

В основе такого предположения лежит характер изменения абсолютных приростов. При общем среднем абсолютном приросте 10,9 mотклонения по отдельным годам не столь значительны: -0,7mв 2007 г. и +0,6mв 2008 г.

Но при наибольшем абсолютном приросте в 2008 г. (+11,5 m) в 2009 г. было снижение этого показателя до 10,9m. Эта максимальная интенсивность роста продажи данного продукта в 2008 г. и последующее снижение в 2009 г. отображает показатель темпа наращивания, %: 16,4 < 18,6 > 17,5.

Цепные темпы роста показывают затухание интенсивности реализации данной продукции из года в год: 116,4 > 116 > 113.

Все эти показания анализируемого ряда динамики позволяют сделать предположения о возможном применении в аналитическом выравнивании параболы второго порядка:

.

Таким образом, на основе статистических показателей изменений уровней анализируемого ряда динамики сделано предположение о возможном применении в аналитическом выравнивании исходных данных двух математических функций: прямолинейной и параболы.

Для решения вопроса о том, какая их них является более адекватной, может применяться критерий минимальности стандартной ошибки аппроксимации:

.

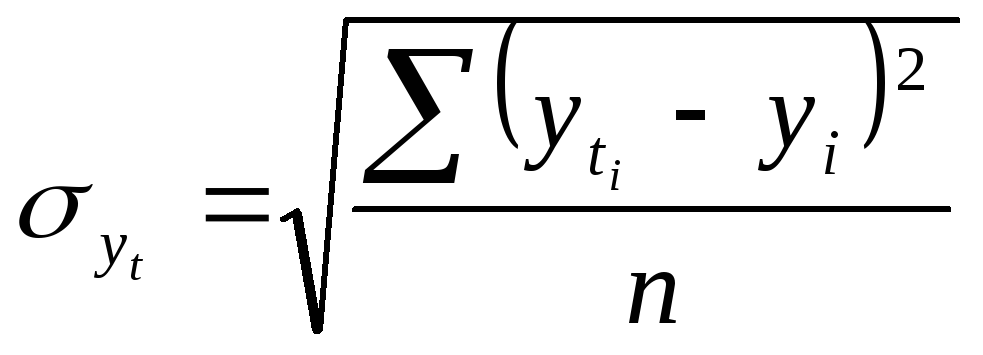Для этого, прежде всего, должны быть решены выбранные математические функции.

Для определения параметров уравнений составляется матрица расчетных показателей (табл. 6).

Таблица 6 – Матрица расчетных показателей при t=0

Год, квартал		ti	ti2	ti4	yi	tiyi	ti2yi
2006	I	-15	225	50625	49,9	-748,5	11227,5
	II	-13	169	28561	75,8	-985,4	12810,2
	III	-11	121	14641	73,9	-812,9	8941,9
	IV	-9	81	6561	48,5	-436,5	3928,5
2007	I	-7	49	2401	48,1	-336,7	2356,9
	II	-5	25	625	92,3	-461,5	2307,5
	III	-3	9	81	93,4	-280,2	840,6
	IV	-1	1	1	55,1	-55,1	55,1
2008	I	1	1	1	50,9	50,9	50,9
	II	3	9	81	106,5	319,5	958,5
	III	5	25	625	108,8	544	2720
	IV	7	49	2401	68,8	481,6	3371,2
2009	I	9	81	6561	60,7	546,3	4916,7
	II	11	121	14641	120,6	1326,6	14592,6
	III	13	169	28561	126,7	1647,1	21412,3
	IV	15	225	50625	70,5	1057,5	15862,5
S	16	0	1360	206992	1250,5	1856,7	106352,9

Рассчитаем параметры линейной функции:

Уравнение линейной функции примет вид:

.

По линейной модели производится расчет теоретических уровней тренда для каждого периода анализируемого ряда динамики :

2006 г.

2009 г.

Полученные теоретические значения уровней тренда записаны в табл. 7.

Рассчитаем параметры для функции параболы второго порядка:

Уравнение параболы второго порядка примет вид:

.

По полученной модели рассчитываются теоретические уровни для каждого периода анализируемого ряда динамики :

2006 г.

2009 г.

Полученные теоретические уровни тренда записаны в табл. 7.

Для определения показаний стандартной ошибки аппроксимации составляется матрица расчетных показателей (табл. 7).

Таблица 7 - Матрица расчетных показателей для определения стандартной ошибки аппроксимации

Год, квартал	ti	yi	Теоретические уровни тренда по моделям (yti)		Отклонения теоретических уровней yti
					от эмпирических
					по моделям yi
			прямоли-нейной функции	параболы второго порядка	прямолинейной функции		параболы второго порядка
					yti - yi	(yti - yi)2	yti - yi	(yti - yi)2
2006
I	-15	49,9	57,7	57,8	7,8	60,5	7,9	61,9
II	-13	75,8	60,4	60,5	-15,4	236,9	-15,3	235,2
III	-11	73,9	63,1	63,2	-10,8	115,8	-10,7	115,3
IV	-9	48,5	65,9	65,9	17,4	301,7	17,4	301,6
2007
I	-7	48,1	68,6	68,6	20,5	420,2	20,5	419,3
II	-5	92,3	71,3	71,3	-21,0	439,7	-21,0	441,4
III	-3	93,4	74,1	74,0	-19,3	374,0	-19,4	376,0
IV	-1	55,1	76,8	76,7	21,7	470,5	21,6	468,1
2008
I	1	50,9	79,5	79,5	28,6	819,2	28,6	816,0
II	3	106,5	82,3	82,2	-24,2	588,0	-24,3	590,4
III	5	108,8	85,0	84,9	-23,8	567,3	-23,9	569,2
IV	7	68,8	87,7	87,7	18,9	357,7	18,9	356,8
2009
I	9	60,7	90,4	90,4	29,7	884,7	29,7	884,5
II	11	120,6	93,2	93,2	-27,4	752,2	-27,4	750,9
III	13	126,7	95,9	96,0	-30,8	948,4	-30,7	945,0
IV	15	70,5	98,6	98,7	28,1	791,6	28,2	796,8
S	0	1250,5	1250,5	1250,5	σyi	8128,3	σyi	8128,3

По итоговым данным табл. 7 определяется ошибка аппроксимации .

Для моделей иошибки аппроксимации одинаковы и равны

.

По критерию минимальности ошибки обе модели предпочтительны. Выбираем трендовую модель, синтезированную на основе прямолинейной функции.

Определение индексов сезонности реализации данной продукции будем осуществлять на базе теоретических уровней тренда, вычисленных по модели .

Теоретические уровни тренда анализируемого ряда динамики изображены на графике (см. рис. 1).

Для определения индексов сезонности используется следующая матрица расчетных показателей (см. табл. 8).

Таблица 8

Год, квартал	yi	yti	yi/ytix100	Год, квартал	yi	yti	yi/ytix100
2006				2008
I	49,9	57,7	86,5	I	50,9	79,5	64,0
II	75,8	60,4	125,5	II	106,5	82,3	129,5
III	73,9	63,1	117,0	III	108,8	85,0	128,0
IV	48,5	65,9	73,6	IV	68,8	87,7	78,4
2007				2009
I	48,1	68,6	70,1	I	60,7	90,4	67,1
II	92,3	71,3	129,4	II	120,6	93,2	129,4
III	93,4	74,1	126,1	III	126,7	95,9	132,1
IV	55,1	76,8	71,8	IV	70,5	98,6	71,5

В таблице 8 определены индивидуальные индексы сезонности , характеризующие отношение эмпирических уровнейк теоретическимдля каждого периода анализируемого ряда внутригодовой динамики. Квартальные колебания за анализируемый период представлены на рисунке 2.

Рисунок 2 – Квартальные колебания реализации

Для элиминирования действия факторов случайного порядка производится усреднение индивидуальных индексов сезонности. Для этого по формуле производится расчет средних индексов сезонности по одноименным кварталаманализируемого ряда внутригодовой динамики:

Iкв.:

IIкв.: