3. Воспользовавшись принципом д’Аламбера и найденными в предыдущем пункте ускорениями найти реакции внешних и внутренних связей механической системы.
Решение. Для определения реакций связей изобразим по отдельности тела механической системы (рис. 17), приложив к ним силы тяжести, реакции внешних и внутренних связей и даламберовы силы инерции. В соответствии с принципом Д’Аламбера, система сил, приложенных к грузу 1 (рис. 17, а), находится в равновесии:
Н.
Составим уравнения равновесия системы сил, приложенных к блоку 2 (рис. 17, б):
,
.
Из последнего уравнения, учитывая, что
,
а момент
найден, следует
Н.
Тогда из двух других уравнений следует
Н;
Н;
Н.
а б
в г
Рис. 17
Составим уравнения равновесия для системы сил, приложенных к катку 3 (рис. 17, в):
,
,
Разрешая
последнее уравнение относительно
,
получим
Н.
Теперь можно определить силу трения сцепления:
Н.
Уравнения равновесия системы сил, приложенных к грузу 4:
;
.
Последнее
равенство уже было использовано при
определении
,
а предыдущее может служить проверкой
полученных результатов:
.
4. Выбрав в качестве обобщенной координаты пройденный грузом 1 путь и составив уравнение Лагранжа второго рода, найти ускорение этого груза.
Решение. Обозначим через q путь, пройденный первым телом за промежуток времени от 0 до t (рис. 18). Тогда уравнение Лагранжа второго рода будет иметь вид
.
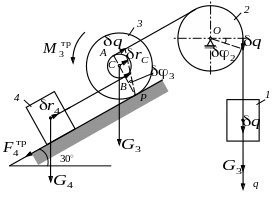
Рис. 18
Кинетическая энергия механической системы была определена в первой части курсовой работы. С учетом принятых обозначений ее необходимо записать следующим образом:
.
Обобщенная сила Q:
,
Здесь вместо
следует написать
,
а выражения возможных перемещений точек
приложения остальных активных сил через
были получены ранее:
.
Подставляя
и
в уравнение Лагранжа второго рода,
получим
.
Откуда
,
т.е. результаты, полученные в первой и
четвертой пунктах решения задачи,
идентичны.
5. Пусть
к центру масс тела 4 прикреплен один
конец пружины жесткости c,
другой конец которой неподвижен. Ось
пружины совпадает с траекторией центра
масс указанного тела (рис. 19). В начальный
момент времени груз 1 был отклонен
от положения статического равновесия
на
и ему была сообщена начальная скорость
.
Определить частоту и период малых
свободных колебаний механической
системы с одной степенью свободы,
пренебрегая силами трения и силами
сопротивления; найти уравнение движения
груза 1
,
приняв за начало отсчета положение
покоя груза 1 (при статической
деформации пружины); найти амплитуду
колебаний этого груза.
Решение. Как и ранее, для решения задачи воспользуемся уравнением Лагранжа второго рода, выбрав в качестве обобщенной координаты перемещение груза 1 из положения статического равновесия.
Кинетическую энергию механической системы представим в виде
,
где а = 4,72m = 23,6 кг – коэффициент инерции системы тел. Так как в пятой части задания не учитываются силы трения скольжения и трения качения, обобщенная сила примет вид
.
Сила упругости
определяется равенством
,
где динамическая деформация пружины в
данном задании равна перемещению центра
масс груза 4:
.
Выражая, как и ранее, возможные перемещения через , получим:
.
Статическая
деформация пружины может быть найдена
из условия равновесия механической
системы в обобщенных силах:
.
м.
Учитывая последнее равенство, обобщенную силу Q можно представить в виде
,
где
Н/м – коэффициент жесткости механической
системы.
Рис. 19
Теперь несложно найти круговую частоту и период собственных колебаний:
с-1,
с.
Амплитуда
колебаний А и начальная фаза
колебаний α определяются из начальных
условий:
;
.
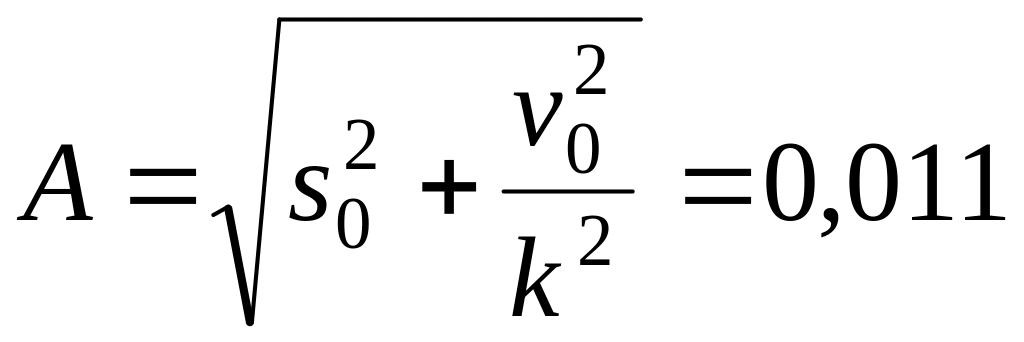м,
Уравнение движения груза 1:
.
*
В вариантах 15, 16,
19, 27 – 29 для того, чтобы система уравнений
стала замкнутой, необходимо дополнительно
задать
– горизонтальную
составляющую реакции оси вращения
третьего тела. Будем предполагать, что
.