
Ответ на вопрос 8
Определение.
Частичной последовательностью или подпоследовательностью последовательности (1)называется любая последовательность вида
{xn1, xn2, …, xnk, …}, в которой номера n1<n2<…<nk<… образуют строго возрастающую последовательность, при этом nk k, k=1, 2, …
Любая подпоследовательностьсходящейся последовательностисходится и имеет тот же предел.
Доказательство.
Пусть
{xn}
сходится
 а
а
 0
0
 N
n>N:
│xn-а│<
и пусть { xn}
N
n>N:
│xn-а│<
и пусть { xn} -
произвольная подпоследовательность
последовательности {xn}.
-
произвольная подпоследовательность
последовательности {xn}.
Докажем, что xn=а.
Так
как {nk}
строго возрастает и
 :
nk
k,
то по теореме §5 {nk}
стремится к +
:
nk
k,
то по теореме §5 {nk}
стремится к + 0,
а значит и для E=N>0
номер K такой, что
k>K:
nk>N
0,
а значит и для E=N>0
номер K такой, что
k>K:
nk>N
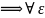 >0
>0
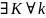 >K:
│xn-а│<
а=
>K:
│xn-а│<
а= xnk.
xnk.
Число
 называется
частичным
пределом{xn},
если
{xnk}
– её подпоследовательность такая, что
xnk=
называется
частичным
пределом{xn},
если
{xnk}
– её подпоследовательность такая, что
xnk=
Определение.
Нижним
пределом{xn}
называется
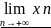 =infМ.
=infМ.
Верхним
пределом{xn}
называется
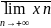 =supМ.
=supМ.
М –ограниченно снизу и неограниченно сверху.
Тогда
по определению
=infМ,
а
=+ .
.
М – ограниченно сверху и неограниченно снизу.
Тогда
по определению
=supМ,
а
=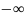 .
.
Ответ на долбаный вопрос 9
Предельный переход в неравенствах.
Теорема
1. Если, начиная с некоторого N, все xn ³
b, то
![]()
Следствие.
Если, начиная с некоторого N, все xn ³ yn,
то
![]() .
.
Важное замечание. Заметьте, что если, начиная с некоторого N, все xn > b, то , то есть при предельном переходе строгое неравенство может перейти в нестрогое.
Теорема 2. («Теорема о двух милиционерах») Если, начиная с некоторого N, выполнены следующие свойства
1.
![]() ;
;
2![]() .
,
.
,
то
существует![]() .
.
Ответ на вопрос 10
Монотонные последовательности.
Теорема.
Любая монотонная ограниченная последовательность сходится.
Доказательство.
Пусть {xn} возрастает и ограничена сверху, то есть x1 x2 … xn … и В n: xn В.
Так как множество {xn} всех элементов последовательности ограниченно сверху, то sup{xn}=а.
Докажем, что xn=а.
sup{xn}=a 1) n: xn а
2)
0
N:
xn>а-
,
а в силу возрастания {xn}
n>N:
а-
<xN
xn
а<а+
а-
<xn<а+
│xn-а│<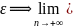 xn=а.
xn=а.
2) 1)
2. Пусть {xn} убывает и ограничена снизу.
Тогда {-xn} возрастает и ограничена сверху. В самом деле x1 x2 … xn … - x1 - x2 … - xn …
{xn}ограничена
снизу
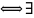 А
n:
А
xn
-
xn
-А
{-xn}
ограничена сверху и возрастает. Тогда
по доказанному в п.1
А
n:
А
xn
-
xn
-А
{-xn}
ограничена сверху и возрастает. Тогда
по доказанному в п.1
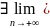 (-xn)=-а=sup{-xn}.
А тогда а=
xn=inf
{xn}.
(-xn)=-а=sup{-xn}.
А тогда а=
xn=inf
{xn}.
Ответ на вопрос 11
Критерий Коши сходимости числовой последовательности.
Теорема.
Числовая последовательность сходится тогда и только тогда, когда она удовлетворяет следующему условию Коши:
0 N=N( ) n>N m>N: │xn-хm│< или
0 N=N( ) n>N и p – натурального: │xn+p - хn│< .
Доказательство.
1.Необходимость.
{xn}
сходится
 а
0
N
n>N:
│xn-
а│<
.
а
0
N
n>N:
│xn-
а│<
.
Возьмём произвольное 0, зафиксируем его и проверим выполнение условия Коши.
{xn}
сходится
а
0,
а значит и для нашего фиксированного
 >0,
N
n>N:
│xn-
а│<
.
>0,
N
n>N:
│xn-
а│<
.
Возьмём произвольные n>N и m>N и рассмотрим │xn- хm│=│xn-а+а - хm│ │xn- а│+│xm- а│< + = , т.е. условие Коши выполнено.
2.Достаточность.
Пусть
{xn}
удовлетворяет условию Коши
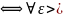 0
n>N,
0
n>N,
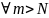 :
│xn-
хm│<
.
:
│xn-
хm│<
.
Докажем, что {xn} сходится.
{xn}
удовлетворяет условию Коши
0,
а значит и для
=1>0
N=N( )
n>N
и
m>N:
│xn-
хm│<
.
)
n>N
и
m>N:
│xn-
хm│<
.
Пусть
m=N+1>N: │xn-
хN+1│<1
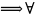 n>N:
xN+1
-1<xn<xN+1+1
n>N+1:
xn
(xN+1
-1, xN+1+1).
n>N:
xN+1
-1<xn<xN+1+1
n>N+1:
xn
(xN+1
-1, xN+1+1).
Вне этого интервала могут находится х1, х2, …, хN.
Пусть А=min{х1, х2, …, хN, xN+1-1}
B=max{х1, х2, …, хN, xN+1+1}
Тогда n, n=1, 2, …: xn [А, В] {xn} – ограничена, а тогда по теореме Больцано-Вейерштрасса (§9) из {xn} можно выделить сходящуюся подпоследовательность {xnk}.
{xnk} сходится а: а= xnk.
Докажем, что а= xn.
По условию Коши, 0, >0, N n>N m>N: │xn- хm│< .
Положим m=nk k>N. Тогда xnk - <xn<xnk+ .
Устремим
k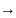 +
.
Тогда по теореме 1 §4 (предельный переход
в неравенствах для одной последовательности)
получаем а-
+
.
Тогда по теореме 1 §4 (предельный переход
в неравенствах для одной последовательности)
получаем а- xn
а+
xn
а+ │xn-
а│
│xn-
а│ <
│xn-
а│<
<
│xn-
а│< а=
xn.
а=
xn.
Определение.
Последовательность {xn}, удовлетворяющая условию Коши, называется фундаментальной.
Из критерия Коши следует, что числовая последовательность сходится тогда и только тогда, когда она фундаментальна.
