Уравнение движения жидкокристаллической среды

Уравнение для временной производной плотности жидкости есть уравнение непрерывности:

(5)

Отметим, что этим уравнением, по существу, определяется гидро­динамическая скорость как плотность потока вещества, отнесен­ная к единице его массы.

Уравнение для временной производной скорости есть дина­мическое уравнение:

(6)

где F —сила, действующая на единицу объема. Объемные силы мо­гут быть представлены в виде тензорной дивергенции:

где -тензор напряжения.

Тогда динамическое уравнение запишется в виде:

(7)

Вид тензора напряжений будет установлен ниже.

Наконец, остается еще уравнение для энтропии. В отсутствие диссипативных процессов движение жидкости было бы адиабатичным, причем адиабатичным в каждом элементе жидкости, ко­торые передвигались бы со своими постоянными значениями энтропии. Уравнение, выражающее сохранение энтропии, запи­сывалось бы просто в виде уравнения непрерывности для нее:

где S — энтропия единицы объема, a vS — плотность потока энтропии ). При учете диссипативных процессов энтропийное уравнение имеет вид:

(8)

Здесь R — так называемая диссипативная функция; 2R/T опре­деляет скорость возрастания энтропии ); она представляет собой квадратичную форму, составленную из компонент тензора v_{i k} и векторов h и градиента температуры . Вектор же q — плотность потока тепла, связанного с теплопроводностью. Компоненты этого вектора -линейные функции компонент вектора градиента температуры:

(9)

В нематической среде тензор коэффициентов теплопроводности x_ikимеет две независимые компоненты и может быть представлен в видe:

(10)

где и описывают теплопроводность в продольном и попе­речном (по отношению к n) направлениях.

Закон сохранения энергии в гидродинамике выражается уравнением вида:

(11)

где Е — плотность внутренней энергии, a Q — плотность потока энергии. Плотность энергии Е = Е₀ +E_d , где Е₀ (р, S) отно­сится к недеформированной, однородной среде, а энергия Е_d свя­зана с искажением поля n (r). Согласно сказанному величина Е_d совпадает со свободной энергией F_d , с той лишь разницей, что модули упругости K_1, K_2, K₃ подразу­меваются выраженными через плотность и энтропию, а не тем­пературу.

Закон сохранения энергии содержится, конечно, в уравнениях движения. Мы же воспользуемся им для установления связи между введенными выше функцией R, тензором и вектором N.

Раскроем производную по времени в уравнении (11) с уче­том термодинамических соотношений:

, где химический потенциал. Имеем:

(12)

Рассмотрим отдельно последний член. Введя обозначение пишем:

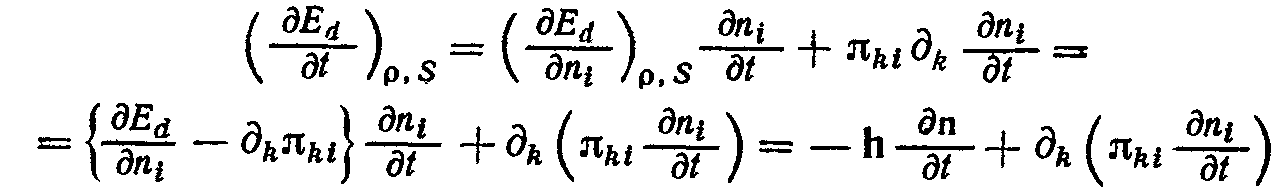
(вместо H здесь написано h, поскольку продольная часть Н сразу выпадает ввиду равенства n dn/dt = 0). Подставив сюда dn/dt из (3), пишем:

и после выделения еще одной полной дивергенции:

(13)

где (14)

Здесь и ниже мы не выписываем полностью выражение под зна­ком дивергенции с целью уменьшения громоздкости формул. Эти члены (к которым мы вернемся еще в конце параграфа) не существенны для решения поставленного вопроса. Выражение (14) можно представить в виде:

(15)

где

(16)

При преобразовании использовано равенство:

Определение тензора неоднозначно: выражение (15) не изменится при добавлении к любого слагаемого вида , где — произвольный тензор, антисимметричный по послед­ней паре индексов .Хотя тензор (16) не симме­тричен, он может быть приведен к симметричному виду прибавле­нием члена указанного вида с надлежащим образом подобранным тензором .Фактическое проведение этой, довольно громоздкой, операции отложим до конца параграфа, а сейчас продолжим вывод уравнений движения, предполагая симметризацию уже произведенной.

Подставив (15) в (13) и выделяя в одном из членов пол­ную дивергенцию (с учетом симметричности ), получим:

(17)

Наконец, подставим в (12) фигурирующие там производные по времени из (5), (7—8) и (17), причем частную (при по­стоянных р и S) производную от Е выразим через полную произ­водную согласно:

После ряда преобразований (выделения полных дивергенций) получим в результате:

(18)

где и связано с формулой:

(19)

а давление введено согласно термодинамическому определению:

(20)

( — термодинамический потенциал единицы объема ве­щества); как и должно было быть, им определяется изотропная часть тензора напряжений.

Сравнив (18) с уравнением сохранения энергии (11), мы видим, что

(21)

Эта функция определяет вызванное диссипативными процессами увеличение энтропии. Ясно поэтому, что введенный в (19) тензор представляет собой диссипативную («вязкую») часть тензора напряжений. Тензор же в (21) не входит; он пред­ставляет собой недиссипативную (помимо связанной с давлением) часть тензора напряжений ), специфическую для нематической (в отличие от обычной) жидкости.

Обратим также внимание на то, что в диссипативную функцию не входит коэффициент .Хотя описываемый этим безразмерным коэффициентом эффект имеет явно кинетическую (а не термодина­мическую) природу, он не диссипативен ).

Плотность объемных сил в движущейся нематической среде:

В неподвижной равновесной (хотя и деформированной) среде F' = 0, а согласно условию равновесия и h = 0. Согласно (14-15) при этом сила:

Если считать модули упругости постоянными, не зависящими от р и S величинами, то и тогда сила F = Но в равновесии должно быть также и F = 0.

Отсюда следует, что (в указанном предположении) распределение давления вдоль находящейся в равновесии нематической среды дается формулой ):

(22)

Произведем теперь в явном виде упомянутую выше операцию симметризации тензора . Прежде всего, вычислим в явном виде антисимметричную часть этого тензора. При вычислении разности надо учесть, что выражение:

симметрично по индексам i, k. Проверить эту симметрию непо­средственно нелегко. Проще сделать это косвенным путем, вос­пользовавшись тем, что энергия E_d — скаляр и тем самым инва­риантна относительно произвольных вращений системы коорди­нат. При бесконечно малом повороте на угол координаты пре­образуются как

т.е.

Для изменения вектора n и тензора d_kn_i имеем соответственно:

Инвариантность функции Е_d при этом повороте означает, что . Поскольку — произвольный антисимметричный тензор, то отсюда следует, что — симметричный тензор, что и требовалось доказать.

Имея это в виду, легко привести антисимметричную часть тензора к виду с тензором:

После этого симметризованный тензор получается непосред­ственно по формуле . После некоторых приведений получим:

(23)

Отметим, что это выражение фактически содержит только попереч­ные (по индексу k) компоненты тензора . Если представить последний в виде:

(так что) , то в (23) останутся только члены с .Наконец, вернемся к членам с полными дивергенциями, кото­рые мы до сих пор не выписывали. Сравнив (18) с (11), видим, что выражение, стоящее под знаком div в совокупности этих членов, определит собой плотность потока энергии. Приведем здесь получающийся таким образом окончательный результат:

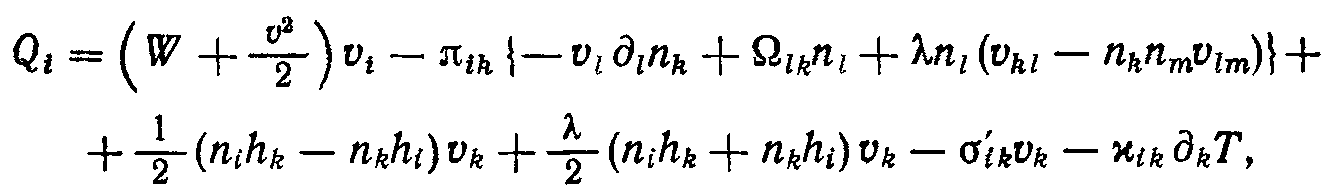(24)

где W = р + Е — тепловая функция. Первый член совпадает с выражением потока энергии в гидродинамике обычной жидкости.